对流层参数估计策略对PPP精度影响分析

闫志闯，楼 楠，李 婧

(西安测绘总站，陕西 西安 710054)

精密单点定位技术是当今GNSS领域的研究热点，它是采用事先确定的高精度卫星轨道和钟差以及双频载波相位和伪距观测量进行单点定位的技术。采用该技术，在全球范围能够使用单台GPS双频接收机获取毫米至厘米级精度的静态坐标或是厘米和分米级的动态坐标[1]。该技术在高精度导航定位、坐标框架维持、时间传递、对流层延迟参数研究、大气延迟提取等领域得到广泛应用。

对流层延迟是精密单点定位中的重要误差源。对流层是指地面向上约40 km范围内的大气层，约占大气层总质量的99%，也是各种气象现象出现主要的区域。一般将对流层天顶总延迟分为静力学延迟(有时称为干延迟)和湿延迟，前者约占总延迟量的90%，可以通过实测的气压和气温精确计算，后者由于大气中水汽变化较大，相应的模型计算精度有限[2]。因此，在精密单点定位中，对流层湿延迟改正成为一个重要的误差源，尤其是当卫星高度角较低时，不仅测量噪声较大，对流层延迟也较大。通常，将对流层湿延迟天顶分量作为一个待估参数，在精密单点定位中一并解算。

1 基本原理

1.1 精密单点定位观测模型

精密单点定位通常需要双频伪距和载波组合观测，其双频消电离层组合表示为

(1)

式中:PC为双频伪距消电离层组合观测量；LC为双频载波消电离层组合观测量；ρ为星地间距离；amb为非差模糊度参数，由于进行消电离层组合，因此模糊度失去整数特性，后面作浮点解进行估计；dTrop为星地连线方向对流层改正延迟；δtr为接收机钟差改正；δts为卫星钟差改正；drel为相对论延迟改正；dgra为引力延迟改正；dwind为相位缠绕改正；ΔPC为双频伪距消电离层组合的测量误差；ΔLC为双频载波消电离层测量误差。

1.2 对流层延迟改正基本模型

卫星导航定位中的对流层延迟通常是泛指电磁波信号在通过高度在50 km以下的中性大气层时所产生的信号延迟。对流层延迟改正与信号传播路径的气压、温度、湿度等气象因素密切相关。通常，对流层延迟改正模型包括气象因素计算模型、对流层延迟模型和映射函数模型等。其中气象因素计算模型可以采用标准大气模型或是全球大气温度模型等；对流层延迟模型则有众多模型选择，比较霍普菲尔斯模型、萨斯塔莫宁模型和勃兰特模型等；映射函数模型有GMF全球映射函数模型等。

dTrop=ztdry×dmap+ztwet×wmap.

(2)

式中:ztdry为天顶干延迟，dmap为干延迟函数；ztwet为天顶方向湿延迟，wmap为湿延迟映射函数。对流层模型，干分量部分能够较好改正，湿分量部分一般能够改正70%左右对流层影响，但剩余部分的影响仍然存在，尤其是对于高精度定位而言，需要进一步改正。通常的改正方法增加待估参数，在定位过程中解算。增加待估参数后，

dTrop=ztdry×dmap+(ztwet+XTrop)×wmap.

(3)

1.3 对流层参数估计策略

对流层参数在定位中作为待估参数进行处理，根据参数定义不同，有多种处理方式。假设一个测站观测24 h，则在观测时间段内，认为对流层延迟是一个常数，定义如下

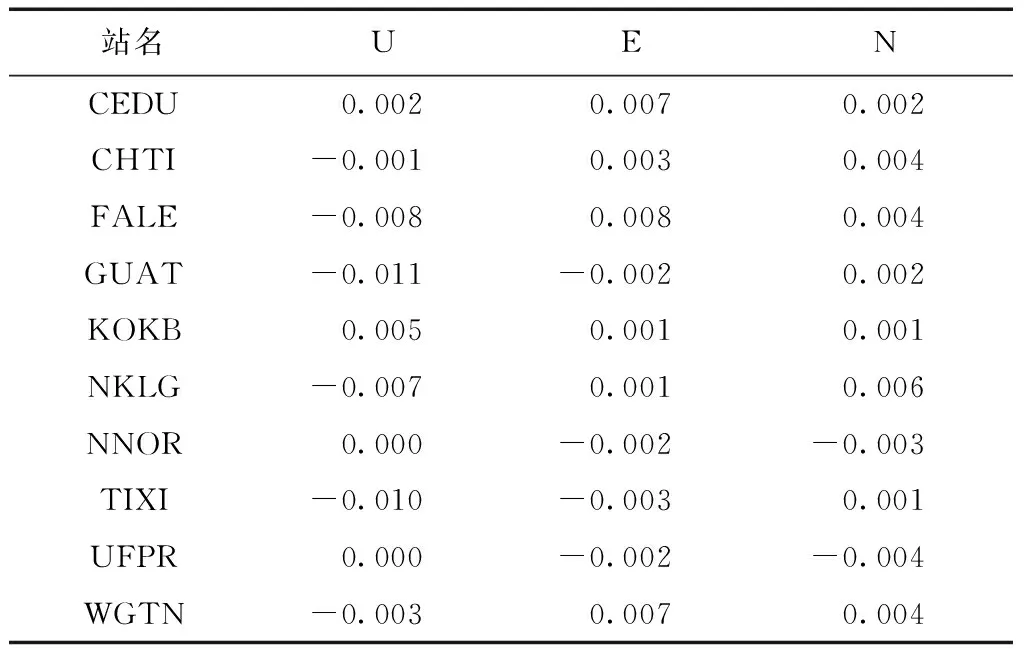
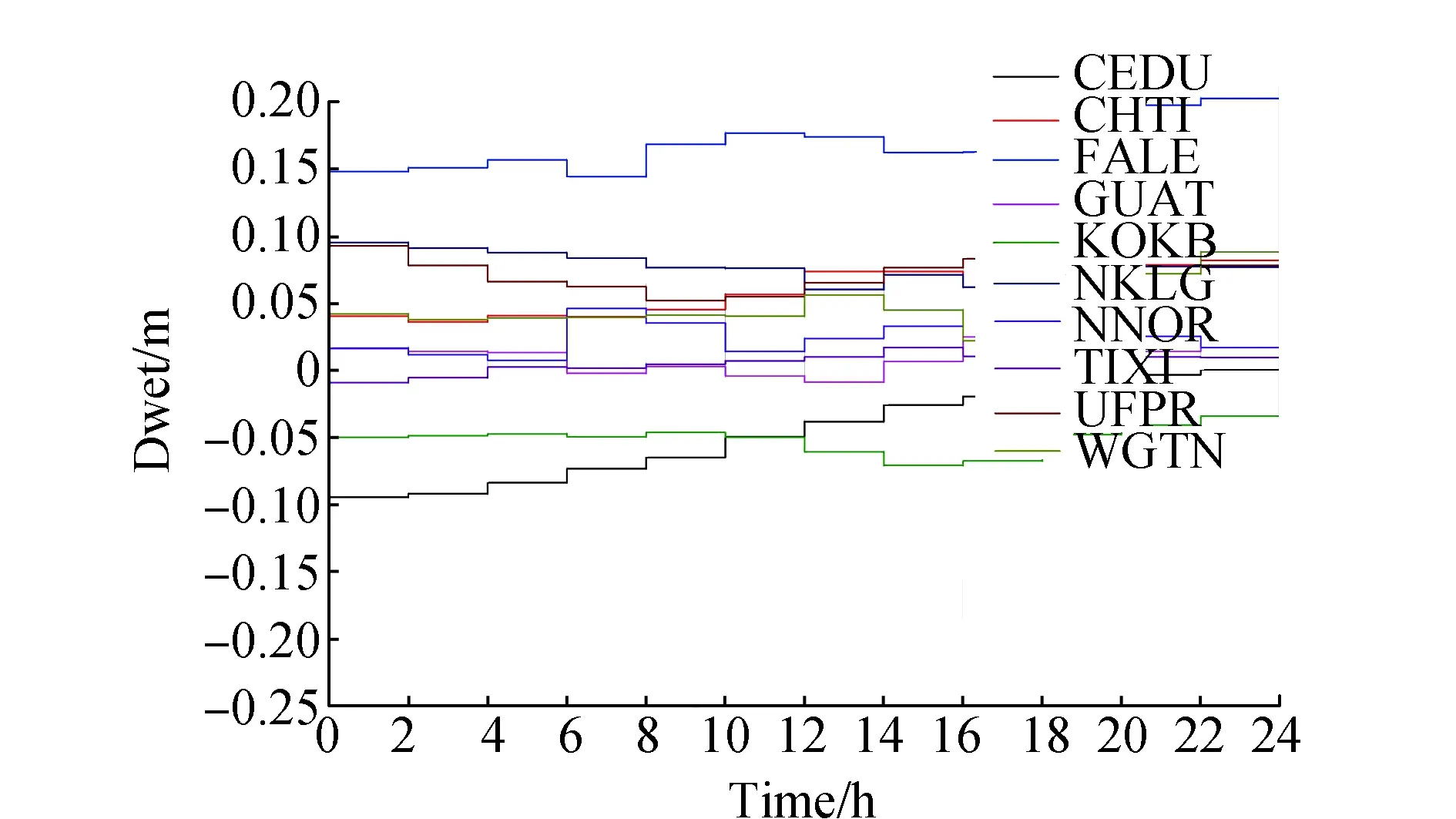
XTrop(t)=XTrop,0

(4)

在观测时段内，对流层改正参数XTrop保持不变。可以对其进行分段处理更好模拟一天变化，从而引入分段常参数模型，定义如下

(5)

式中:分段常参数模型将整个对流层天顶湿分量延迟残余分为n个分段常参数，在精密定位过程中进行估计，不同时间段的改正量之间没有任何关系。

由于整个对流层延迟是一个变化连续且缓慢的过程，分段模型相对常参数模型要好，但仍然与实际情况不太相符。鉴于此，顾及相邻段对流层参数之间的近似关系，可以用一个随机漫步过程来模拟。

利用中国水利水电科学研究院推送的MODIS数据产品以及实时下载的MODIS L1B遥感数据，结合地面观测数据、遥感解译土地利用、作物种植结构等资料，调用研发的旱情遥感监测模型，按区域特点、作物生长期、土壤类型等影响因素率定模型参数，遥感反演得到干旱监测指数和土壤含水量图，参考土壤相对湿度旱情等级划分标准(SL 424—2008)划分干旱等级，并套合耕地、作物类型图，统计分析受旱耕地、作物面积，实现黑龙江省受旱区的农业旱情遥感监测，为更全面、细致地掌握本省旱情总体情况提供信息支撑。

XTropi+1=XTropi+Wi+1.

(6)

式中：Wi+1为第i+1段对流层参数的过程噪声，其均值为0，方差为

(7)

采用分段常参数模型，不同段之间采用随机漫步过程进行约束。

通常在采用滤波算法的精密单点定位中使用，如果是最小二乘批处理算法，则构建虚拟观测量，将其变形为

(8)

(9)

2 数据实验及分析

2.1 实验数据及策略

选取2015年年积日005D且全球均匀分布的10个IGS测站的原始观测数据进行试验，卫星星历和钟差采用IGS发布的精密星历和5 min采样间隔的精密钟差。原始观测数据采样率为30 s，这里进行降采样处理，将其降为5 min采样间隔。采用双频消电离层组合及最小二乘批处理方法进行精密单点定位，待估参数包括测站坐标、接收机钟差、模糊度参数和对流层天顶方向湿延迟残余改正。分别采用单参数模型、分段常参数模型和附加随机漫步过程约束的分段常参数模型三种对流层参数估计策略进行上述测站的事后静态精密单点定位实验。整个数据实验在卫星精密定轨定位与重力场恢复系统(Satellite Precise Orbit Determination And Gravity Recovery System, SPODAGRS)上进行。该软件是在参考GPSTK等现有GNSS数据处理软件基础上，采用标准C++语言独立编写的一套卫星精密定轨定位与重力场恢复软件系统。对流层参数设置如表1所示。

2.2 实验结果与分析

以IGS周解作为测站坐标真值，比较上述三种对流层参数估计策略下精密单点定位结果在UEN方向与真值之间的差异，比较结果如表2、表3、表4所示。

表1 对流层参数估计策略设置

表2 单参数模型PPP结果 m

表3 分段常参数模型PPP结果 m

表4 附加随机漫步过程约束的分段常参数模型PPP结果 m

由表2可以看出，采用单参数模型进行精密单点定位，定位精度达到厘米级水平，其中U方向精度稍差，与IGS周解最大偏差为0.019 m，E方向最大偏差为0.015 m，N方向差别普遍较小，不超过0.006 m；由表3可以看出，采用分段常参数模型进行精密单点定位，与表2相比，U方向定位精密明显提高，尤其是CEDU和FALE两个测站，U方向与IGS周解之差分别由单参数时的0.019 m和-0.018 m降为0.002 m和-0.008 m，改进达0.01 m；由表4可以看出，附加随机漫步过程约束的分段常参数模型定位结果与分段常参数模型定位结果基本一致，二者仅有0.002 m左右差异。

表4中的结果介于表2和表3之间，与选择的过程噪声参数密切相关，若过程噪声为0，附加随机漫步过程约束的分段常参数模型退变为单参数模型；若过程噪声为无穷大，退变为分段常参数模型。三种模型所估计对流层天顶湿分量残余随时间变化如图1、图2和图3所示。

图1 单参数模型对流层天顶湿分量残余

图2 分段常参数模型对流层天顶湿分量残余

图3 附加随机漫步过程约束的分段 常参数模型对流层天顶湿分量残余

由图1可以看出，在24 h内，每个测站对流层天顶湿延迟残余是一个常数，不同测站相应改正值不同，最小在-0.05 m左右，最大在0.175 m左右，表明仅采用萨斯塔莫宁对流层模型进行干湿分量改正无法完全改正对流层延迟，因而估计对流层天顶湿延迟残余是必要的。

由图2和图3可以看出，当采用分段常参数模型时，每个测站的对流层天顶湿延迟残余在活跃期内是一个常数，24 h范围内呈现阶梯状变化，且两幅图差异不明显，但与图1相比，有显著差异，尤其是CEDU测站和FALE测站，分段常参数模型与单参数模型差异较大，也进一步表明分段模型能够更好模拟相应测站的对流层实际情况，从而使得精密单点定位精度有明显提高。

3 结 论

本文利用分布全球的10个IGS站观测数据，分别基于对流层单参数法、分段常参数法和附加随机漫步过程约束的分段常参数法进行事后静态精密单点定位实验，获取厘米级精度的测站坐标，同时分析了3种对流层估计策略对测站定位精度的影响，可以得出以下结论：

1)无论采用哪种对流层估计策略，均能获取厘米级精度的测站坐标；

2)采用分段常参数模型的对流层估计策略明显优于单参数模型，对U方向定位精度影响可达0.01 m；

3)附加随机漫步过程约束的分段常参数模型对定位精度的影响介于单参数模型和分段常参数模型之间，其过程噪声越接近0，定位结果越接近单参数模型，过程噪声越接近无穷大，定位结果越接近分段常参数模型；

4)分段常参数模型与附加随机漫步过程约束的分段常参数模型解算的对流层天顶湿分量残余改正呈阶梯状变化，变化越明显，则对定位精度影响越显著。