敢于放手 无问西东

郭新俊

[摘  要] 求线段和最小值问题是初中阶段的重要考点也是难点. 文章旨在解决一个含三个动点的线段和最小值问题，利用化动为静的思想先固定其中一个点，再利用转化的数学思想将其转化为含两个动点的线段和最小值问题[1]，最终依托点与直线的连线中垂线段最短得以解决.

[关键词] 线段和;对称点;垂线段;转化

在学习完苏科版八年级上册第二章轴对称图形时，一天数学课代表来办公室咨询一个含有三个动点求线段和最小值问题. 从学习新课到讲解习题课，学生遇到的多是含一个动点或者两个动点的线段和最小值问题，像这种含三个动点的线段和最小值问题，对于学生来说难度过大. 但笔者所带的这个班级学生基础较好，能力较强，有好几个对数学十分感兴趣的学生建议将此题拿到班级讲解. 恰逢笔者所在学校的教研组正实施初中数学“综合与实践”教学的校本化研究，需要笔者开设一节活动课，于是经过一段时间的构思，笔者在校内上了关于此题的一节活动课，现将其部分课堂实录及一些不太成熟的思考整理出来，请同仁们批评指正.

教学实录

1. 原题呈现

教师先用几何画板出示题目，请同学们先思考.

如图1，请在△ABC的三边AB，AC，BC上分别确定一点E，F，D，使△DEF周长最小.  （学生思考几分钟基本上一脸茫然）

[图1][B][C][A]

2. 洞察本质

师：求三角形周长最小值在数学中属于什么问题？

生1：线段最小值问题.

生2：线段和最小值问题.

师：补充得很好，解决这类问题最终的落脚点在哪里？

生3：两点之间线段最短.

师：正确，还有补充的吗？

生4：点与直线的所有连线中，垂线段最短.

师：非常好.

3. 经验回顾

师：请你写出以前学过的类似的问题并思考解决方案. （学生思考并在学习单上书写共5分钟）

生5：我想到的是“将军饮马”问题，如图2，在直线l上找一点P，使得PA+PB最小.

[图2][l][A][B]

师：非常好，你是如何解决这个问题的？

生5：如图3，作点A关于直线l的对称点A′，连接A′B交直线l于点P，点P即为所求.

[图3][l][A][B][P][A′]

师：很好，你是怎么想到的？

生5：两点之间线段最短.

师：能具体展开解释吗？

生5：额……

生6：这里有个转化的数学思想，通过对称变换将同侧PA+PB转化为异侧PA′+PB，从而实现两点之间线段最短.

师：非常棒，请坐. 哪位同学能解释为什么此时PA+PB就是最小的？

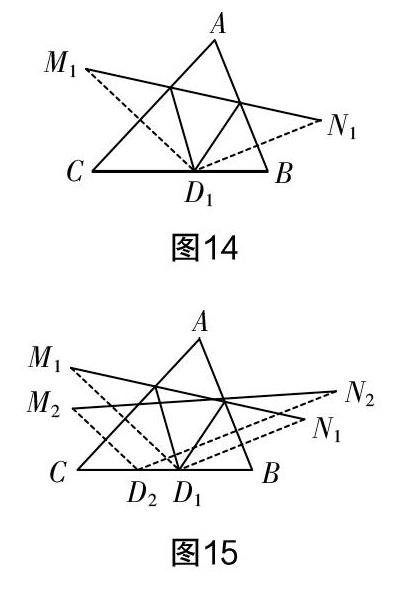
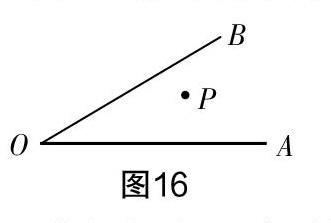
生7：如图4，在直线l上任意取一点P′，根据两点之間线段最短或者三角形两边之和大于第三边易证：A′B

[图4][l][A][B][P][A′][P′]

师：好，思维很缜密. 还有想到别的问题的吗？

生8：我想到的是这样一个题目：如图5，点P在∠AOB内部，在OA，OB上分别找一点M，N，使得△PMN周长最小.

[图5][A][B][P][O]

师：这是一个含有两个动点的线段和最小值问题，你如何解决这个问题？

生8：如图6，过点P分别作OA，OB的对称点P1，P2，连接P1P2分别交OA，OB于点M，N. 点M，N即为所求.

[图6][A][B][N][O][M][P][P2][P1]

师：生8找到的△PMN的周长是不是最小，为什么？

生9：是的，如图7，在OA，OB上再分别任意找一点M′，N′，根据两点之间线段最短不难说明PN′+M′N′+PM′>PP，而PP的长即为△PMN的周长.

师：两位同学说得都非常好，那你们有谁能告诉我，为什么要向两边作对称点？

生9：记模型背公式. （全班一阵欢笑）

师：还有哪位同学有想法的？（全班陷入一片寂静）

师：还记得刚才在解决将军饮马问题时所考虑的数学思想方法吗？（有几个学生在下面小声答道：转化）

师：对，就是转化，这时我们也可以将它转化为将军饮马问题，再想想. （这时有一位同学很激动地举起手）

生10：如图8，先在OB上任意找一点固定为N，此时问题就转化为了将军饮马问题，原△PMN的周长就是图9中线段PN+PN的和. 由于点N1位置的任意性，也可以另取一点N，如图10，此时原△PMN的周长就是图中线段PN+PN的和，这样的点N有无数个.

[图8][A][B][P][O][N1]

[图9][A][B][P][O][N1][M1][P2]

[图10][A][B][P][O][N1][M1][P2][N2][M2]

师：这位同学给我们做了一个十分漂亮的转化，但是问题还是没解决啊！少年们还需努力啊！（同学们都被逗乐了）

师：现在把OA擦去，如图11，你有新的发现吗？

生11：原△PMN的周长最小就是求在OB上找一点N，使PN+PN最小，这又是将军饮马问题，作法如图12. 作点P关于直线OB的对称点P，连接PP交直线OB于点N，交直线OA于点M，点N，M即为所求，如图13.

师：非常好，此处应该有掌声！（全班鼓掌）

4. 解决问题

师：同学们，回顾以上求解过程，带着解题经验让我们来看今天的问题，你有什么新的想法？

生12：本题有三个动点，我们也可以像刚才一样先在BC上固定一个点D，原题就变成在AB，AC上分别确定一点E，F，使△DEF周长最小，从而变成了生8想到的那个题目. 作法如图14，作点D关于直线AB，AC的对称点M，N，连接MN，线段MN的长就是所求三角形的周长. 当然这样的D也不止一个，还可以找D，如图15，线段MN的长就是所求三角形的周长. 也就是说，求三角形的最小周长就是找一条最短的线段MN，这是我想到的.

师：说得太好了，他用了一个类比的数学思想带我们朝着目的地前进了一大步. 正如他所说，求三角形的最小周长就是找一条最短的线段MN，如何找呢？（同学们又一次陷入了疑云中）

师：我们先思考以上那些线段MN有什么共同之处？先独立思考完，小组之间交流一下. （同学们进入激烈的讨论中，此时教师在巡视的过程中依然没有发现有價值的成果）

师：请同学们看一下我们曾经做过的这个题目，对你有什么启示？（此时教师利用多媒体呈现了一道学生作业中的习题）

习题呈现：如图16，∠AOB及平面内一点P，试画出点P关于直线OA的对称点P1，再画出点P关于直线OB的对称点P2，在画图的过程中你有什么发现？

[图16][A][O][B][P]

生13：我想起来了，把所有的点M和N都和点A连接起来，如图17，这样就得到了无数个以线段MN为底边的等腰三角形.

[图17][B][D1][C][N1][A][M1][D2][N2][M2]

师：很好，还有补充的吗？

生14：这些等腰三角形的顶角都一样大，都等于∠CAB的两倍.

师：棒极了，还有吗？（教师的热情也被点燃了）

生15：这些等腰三角形的腰长都等于相应的线段AD长.

师：完美，顶角相等的等腰三角形底边的长短跟哪个因素相关呢？

生16：腰长（齐声答）.

师：刚才求最短的线段MN就是求什么？

生17：最短的线段AD.

师：线段AD什么时候最短？

生18：垂线段最短（齐声答）.

师：今天你们的表现真太精彩了……

教学板书

[三动点线段和最小][垂线段最短][转化][单动点线段和最小

——将军饮马问题][两点之间线段和最小][比较等腰三角形

的腰长][比较等腰三角形

的底边长][?][双动点线段和最小][转化][?][转化][?][?][?][?][?][图18]

几点思考

1. 放手：基于学生学情

本节课上下来，总体上比较流畅. 首先，得力于对学生学情的充分认识和了解. 笔者在备课时，一直都想着这个班学生的知识掌握情况，哪里可以完全放手，哪里需要适当引导都必须提前预设好. 即在经验回顾环节，笔者成功预设到学生能想到将军饮马问题和含两个动点线段和的问题，这样就自然调动了学生的积极性和主动性. 这样的放手就比教师直接给引例让学生去思考的效果好了许多.

对学情的了解不仅仅是了解全班整体学生的情况，对于每个人的情况也需要关注. 笔者尝试放手将问题交给全班学生探究，以这样的方式完成课堂的教学任务完全没有问题，但是可能会出现一个现象：只有思维好的学生在交流，思维慢一些的学生开始是跟不上节奏，后来就索性沉默，完全是在观看他们的同学“表演”. 这样的探究恐怕只能是少数人的探究，也违背了“非独立不合作探究”的原则. 于是，本着尊重每一位学生，笔者要求在探究之前必须让所有学生先独立思考，可以把思考的结果简要地在学习单上写出来，然后交流，如果独立思考有困难，可以直接讨论. 这样一个小的设计，立刻能让所有的学生都参与进来，而且能得到很多意外的“收获”. 因为有些学生怯于在全班同学面前表达自己的观点，而他们很乐意在学习单上写出来. 记得一次市教研活动上，一位特级教师就强调过：“数学课上要有静悄悄”. 现在想来的确是这样，每一个有深度的问题都需要独立思考时的“静悄悄”，这也是基于学情进行教学设计的一个重要方面.

2. 放手：基于科学理论

课堂上教师的敢于放手不仅要对学情有充分的了解，更要有一定的科学理论作为指导. 美国著名数学家波利亚在他的著作《怎样解题》中说：“我们几乎不可能想出一道全新的题目，它和以前解过的题目既不相像，又无联系. 而且假如有这样的题目存在，它也是解不出来的. 事实上，我们在解题时总是得益于以前曾解过的那些题目，应用它们的结果或者方法，或者我们在解答中所获得的经验.[2]”正如本节课研究的含三个动点的线段和最小值问题，学生虽然刚开始拿到题目有些茫然，但根据波利亚的解题理论，先思考以前研究过的类似的问题以及解决那些问题的策略和方法，再回头看问题学生能很快、很自然地想到，将三个动点中的一个动点先定下来，而去考虑另外两个点，即化动为静的策略. 这样的放手，有着理论知识的指导，学生不仅仅学会了这一题的解法，更是学会了遇到新的问题时的思考方法.

3. 放手：基于有效铺垫

综合实践课基本上是以学生的探究活动为主，但教师也不能从头到尾一味地放手，否则会出现两种情况，要么离本节课主题越来越远，要么在某个环节卡住使得探究活动进行不下去，此时教师给予适当的铺垫就显得尤为重要. 而这一铺垫到底该什么时候给，以什么样的形式给，那就要考验教师的能力了. 著名的维果斯基的“最近发展区理论”强调：教师应着眼于学生的最近发展区，根据学生认知水平，为学生提供带有难度的内容，调动学生的积极性.

为了靠近学生的最近发展区，笔者认为有效的铺垫可以是一个追问、也可以是一道学生做过的习题. 就如同本节课在解决含两个动点的线段和问题时，当被问到为什么要向两边作对称点，同学们都安静了. 笔者提示性地问“还记得刚才在解决将军饮马问题时所考虑的数学思想方法吗？能否也将其转化为将军饮马问题呢？”这时同学们才恍然大悟. 还有一个地方也是本节课最难攻克的障碍：在解决含三个动点的线段和最小值问题时，当学生已经发现了求三角形的最小周长就是找一条最短的线段MN时，笔者的设计是呈现了一道学生之前做过的关于对称性质的习题. 虽然学生通过对此题的回忆也顺利找到了课上的难题的突破口，但笔者还是感觉有些牵强，提示过于明显. 即便如此，本节课还是在下课铃声响起之后而急急忙忙收尾. 紧接着的研讨会上，教研组长问听课的三十多位老师有多少人当时想到如何找最短的线段MN，统计完也只有一半的老师能想到. 所以对于学生来说，思维的要求有些过高了. 当然，如果本节课在上课时间上做适当的调整，将四十五分钟改成一个小时或者干脆两节连上，这样留给学生更多的思考和探究时间，或许孩子们能给我们带来更大的惊喜.

参考文献：

[1]郦兴江. 构建模型提炼策略  层级推进数学思考——以“最短路程问题”为例[J] . 中学数学教学参考，2015（35）.

[2]波利亚. 怎样解题[M]. 上海：上海科技教育出版社，2011.