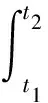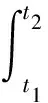种群模型中一类迁移半群的本质谱
(上饶师范学院 数学与计算机科学学院 ,江西 上饶 334001)
本文研究了下面由M.Boulanouar在文献[1-2]中提出的一类种群细胞模型:
(1)
其中r(u,v,v′)表示细胞从v′到v改变时的转变速率,σ(u,v)为总转变截面,且满足
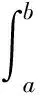
边界条件可表示为:
(2)
这里常数α,β≥0表示每一细胞分裂的平均数。其余符号定义和意义详见文[3-4]。
近年来,对方程(1)的研究工作较少,其中文献[1-2]在L1空间和边界条件,即式(2)中α=0的条件下,研究得到了该模型相应的迁移算子生成正不可约C0半群和该模型相应的迁移方程的解在一致算子拓扑意义下的渐近行为等结果;文献[3]证明了这类模型生成半群的Dyson-phillips展式的9阶余项R9(t)在L1空间上是弱紧的和在Lp(1 它们分别按范数 和 构成Banach空间,且定义Y=L2(J,h(v)dv)为迹空间,其范数: 边界空间为: X0=L2({0}×(a,b);h(v)dv);X1=L2({0}×(a,b);h(v)dv) 下面定义边界算子H为: 且φ0=φ(0,v),φ1=φ(1,v)。设Streaming算子T和碰撞算子K及迁移算子A如下: D(T)={φ∈W|φ0=Hφ1} A=T+K,D(A)=D(T) 其中h(v)为有界可测函数,且满足 假设 其中α(·)∈L([0,1],du),f(·),g(·)∈L2([a,b],dv)。 令σ0=essinf{σ(u,v)}。对φ∈X,λ∈C,ψ∈D(T),考虑方程 (λ-T)ψ=φ (3) 则∀λ:Reλ>-σ0,方程(3)的形式解为: (4) 取u=1,则(4)式为: (5) 根据(4)式和(5)式引入如下算子: 则∀λ:Reλ>-σ0,算子Pλ,Qλ,Dλ和Eλ都是有界正的[3],从而(5)式和(4)式分别为: ψ1=PλHψ1+Dλφ (6) ψ=QλHψ1+Eλφ (7) 令 则当Reλ>λ0时,有 ‖PλH‖<1 (8) 从而算子(I-PλH)-1存在,所以(6)式和(7)式可表示为: ψ1=(I-PλH)-1Dλφ (9) ψ=QλH(I-PλH)-1Dλφ+Eλφ (10) 故由(9)式和(10)式可得: (11) (12) 先引入本文主要结果证明所依据的主要引理。 引理1[5]设T是Hilbert空间X上半群U(t)的生成元,且为一耗散算子,K和K*为X上的有界算子,若存在m∈N和η>ω(U)满足: (λI-T)-1[K(λI-T)-1]是紧的∀λ:Reλ≥η, 则R1(t)(∀t>0)在X上是紧的。 引理2[6-7]设(Ω,Σ,u)正可测空间,S,T是(Ω,u)上的有界算子,若T是(弱)紧算子,且0≤S≤T,则S是(弱)紧算子。 设 假设(O)成立,设边界算子 定理1若算子K为紧算子,则(λI-T)-1K是紧的 ∀λ:Reλ≥λ0。 证明:已知由(8)式知:当Reλ>λ0时,有‖PλH‖<1 ,则 存在常数C>0,使得‖PλH‖≤c<1 ∀λ:Reλ≥λ0。 定理2若算子K为紧算子,则迁移半群的Dyson-phillips展式的n阶余项Rn(t)(n≥1)是紧的且半群U(t)和V(t)具有相同的本质谱和一致的本质谱型。 证明:令算子T产生的半群为U(t),ω表示U(t)的型,则由半群理论知: 由定理1的证明知: (λI-T)-1K为一正算子,则对任意0 (13) 对任意t∈[0,+),ε>0,有 (14)1 准备知识
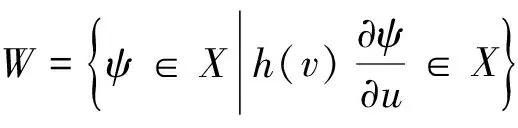
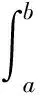
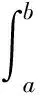
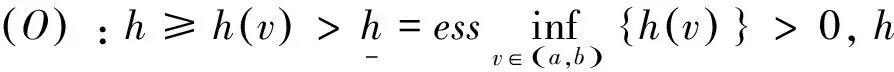
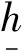
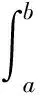
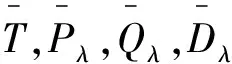
2 主要结果