基于磁导引AGV的路径跟踪控制策略研究*

曾祥苹，刘兴教，栗 江

(1.广州南洋理工职业学院 机电与汽车学院，广州 510125；2.华南理工大学 机械与汽车工程学院，广州 510641)

0 引言

AGV(Automated Guided Vehicle自动导引运输车)，是指装备有电磁或光学等自动导引装置，能够沿规定导引路径行驶，具有安全保护以及各种移载功能的运输小车[1]，属于轮式移动机器人范畴。目前，AGV在导引方式上有磁导引、激光导引、惯性导引和视觉导引[2]，每种导引方式有其自身的应用特点，可根据实际情况灵活选用。本文的磁导引AGV是一种预先在规划路径上铺设磁条，通过车上传感器感应磁条信号进行导航的AGV。

磁导引AGV在驱动转向方式上有单舵轮驱动、双舵轮驱动、四舵轮驱动、双轮差速驱动和麦克纳姆轮驱动等[3]，通过查阅大量文献发现：目前，学者们对磁导引AGV路径跟踪控制的研究主要集中在双轮差速驱动型AGV上，而对前轮舵机转向、后轮速度驱动型磁导引AGV的路径跟踪控制研究甚少。本文则重点对此类驱动方式的AGV进行路径跟踪控制策略研究和设计。

1 磁导引AGV系统结构

AGV在结构上通常由：控制器模块、导航模块、驱动模块、避障模块、通信模块和电源模块共六部分构成[4]。其中控制器模块、导航模块和驱动模块是磁导引AGV实现路径跟踪控制的硬件基础，此处AGV驱动采用前轮舵机转向+后轮电机速度驱动的方式，具体采用磁导航传感器跟踪采集路面预先铺设的磁条信息，然后将这些信息传送给主控制器(单片机)，主控制器经过运算对前轮舵机的转角和后轮速度进行决策控制调整，使AGV沿规定路径行驶。其整体控制结构可分为三层，如图1所示。

图1 路径跟踪控制结构图

2 运动学模型

对磁导引AGV进行路径跟踪控制，实质是对小车行驶方向和速度的控制，并根据路况自动协调方向和速度的关系，减小路径跟踪偏差量。而建立抽象的数学模型是对其进行深入研究的基础，如图2所示是小车的运动示意图。XOY为全局坐标系，相对于车体中心，φ为可控的前轮舵机转角，两前轮随舵机同步转向；两后轮是通过差速器连在后轴上，后轴通过齿轮由直流电机驱动，后轴始终与车体中心轴保持垂直；θ是车体中心与X轴的夹角；前转向轮中心点为Q，后速度驱动轮中心点为H，L为前后轮中心点之间的距离。

假设小车是刚性的且作纯滚动运动，根据几何关系，前后轴中心线速度关系如下：

(1)

式中，VQ为前轴中心点Q处线速度；VH为小车驱动速度。

若以Q点作为反映小车位置的参考点，则在全局坐标系下可用向量P=[XQ,YQ,θ]T表示小车位姿情况，它与小车转角φ及Q点速度之间的关系为：

(2)

(3)

(4)

根据式(2)～式(4)，该磁导引AGV运动方程表示为：

(5)

将式(5)进一步离散化，得到(k+1)时刻小车的位姿：

(6)

式中，k为采样时刻；ΔT为采样时间间隔。

3 路径跟踪控制策略

路径跟踪控制是AGV实现自主导航的基础，而控制算法是实现路径跟踪控制的关键。PID控制是一种较传统的控制方法，但其在使用上具有一定的局限性，尤其对一些较复杂的时变非线性系统控制效果往往不佳。近年来 ，国内外许多学者又提出一些新的智能控制算法，并取得了一定的效果，如文献[1]提出粒子群算法对PID参数进行优化的方法；文献[5]采用模糊控制实现小车路径跟踪控制；文献[6]采用神经网络算法对PID控制器参数进行优化，从而提高路径跟踪精度等；本文的前轮舵机转向、后轮速度驱动型磁导引AGV，其路径跟踪控制是一个较复杂的时变、非线性系统，很难建立其精确数学模型。另外由式(6)可以看出，该磁导引AGV能否以较高的精度沿指定路径行驶，是由当前舵机转角和小车速度共同决定的，两者需协调配合，如当小车行驶速度较快时，舵机转角值应减小；而当小车速度较慢时，可适当增大舵机转角等等；其控制规律可通过人的生活经验总结获得，因此，此处采用模糊控制算法实现前轮舵机转角和后轮驱动电机速度的控制。模糊控制即是一种基于人的操作经验总结出来的控制规则用计算机来实现的自动控制,它区别于经典控制理论的是不需要知道控制系统精确的数学模型,就能够实现有效的控制[7]，具有适应能力强、智能性高和控制实现简单的优点。

此处磁导引AGV路径跟踪控制结构图如图3所示，具体实现过程是将磁导航传感器获得的小车实际位置与理想位置间的偏差量作为输入，经过前轮转向控制器和后轮速度调节控制器协调配合控制，达到实时调整舵机转角和驱动电机速度的目的，使小车能够以较高的精度和稳定性沿给定路径行驶。

图3 路径跟踪控制结构图

3.1 前轮转向模糊控制器设计

模糊控制器在结构上通常由模糊化、模糊推理和解模糊(或清晰化)三部分构成，具体控制过程是将传感器获得的精确输入信号值模糊化，再经过经验总结的控制规则进行模糊推理，最后将得到的模糊结果转换为精确控制量进行输出，驱动执行机构动作。具体设计内容包括：

(1)定义模糊控制器输入、输出量，确定其语言变量及相应论域上的模糊子集

前轮转向模糊控制器实际上是根据小车跟踪路径偏差值实时调整舵机转角，实现小车沿给定路径直行、左转或右转，然而针对前轮舵机转向+后轮速度驱动型磁导引AGV，其位姿同时还受到后轮驱动速度的影响。因此将小车跟踪路径的偏差值E和小车速度V作为该模糊控制器的输入量，舵机转角U作为输出量，构成一个2输入/1输出的模糊控制系统；结合实际的磁导引AGV路径跟踪情况，此处将输入量偏差值E的模糊语言变量定义为：{“负大”，“负中”，“负小”，“零”，“正小”，“正中”，“正大”}={“NB”，“NM”，“NS”，“Z”，“PS”，“PM”，“PB”}，为了提高控制精度将偏差值E的语言变量量化为13个等级，其论域表示为：{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；小车速度V这一输入量的模糊语言变量定义为：{“很慢”，“慢”，“中速”，“快”，“很快”}={“VS”，“S”，“M”，“F”，“VF” }，对应的论域表示为：{0,1,2,3,4,5}；对于输出量舵机转角U，其语言变量也定义为：{“负大”，“负中”，“负小”，“零”，“正小”，“正中”，“正大”}={“NB”，“NM”，“NS”，“Z”，“PS”，“PM”，“PB”}，由于舵机实际转角大小受到小车机械结构及舵机本身最大转角的限制，因此结合实际情况，其论域为[-45°，45°]；对于隶属度函数，本文输入输出均选择较常用的三角形隶属度函数。对应小车偏差值E、速度V和舵机转角U的隶属度曲线如图4所示。

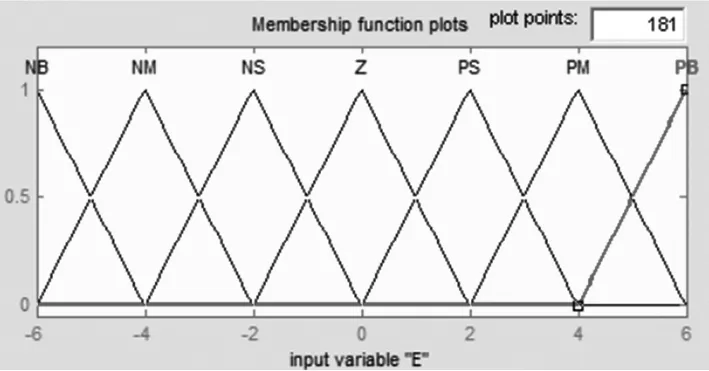
(a)偏差E隶属度函数

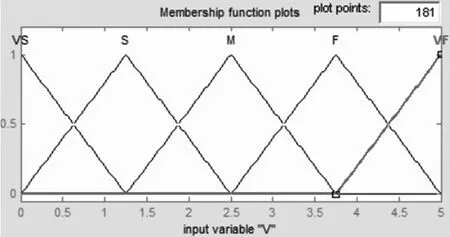
(b)速度V隶属度函数

(c)转角U隶属度函数图4 偏差E、速度V和转角U隶属度曲线

(2)运用模糊推理方法，建立模糊控制规则及对应的模糊关系

制定模糊控制规则是进行模糊控制的关键，它是建立在人的实验、学习和经验总结基础上的，反映了输入量与输出量之间的映射关系。此处对前轮舵机进行转向控制可结合人们驾驶车辆的经验总结其控制策略，具体归纳为以下几点：

①当偏差E>0时，小车相对于给定路径右偏，此时小车应向左转，舵机转角U为负；反之，当偏差E<0时，小车相对于给定路径左偏，此时小车应向右转，舵机转角U为正；而当E=0时，说明小车在给定路径上行驶，舵机转角U为零；

②若偏差E绝对值较大，说明小车此时偏离给定路径较远，则应加大舵机转角U的值，使小车尽快回到给定路径上；反之，若偏差E绝对值较小，说明小车此时距离给定路径较近，应减小舵机转角U的值，提高控制精度和稳定性；

③当小车行驶速度V较快时，应减小舵机转角值U；反之，当小车速度较慢时，可适当加大舵机转角值；

这些控制策略在模糊控制器中需用专门的模糊推理方法进行表达，本文采用马丹尼(Mamdani)的max-min 推理法，即条件语句ifEandVthenU的推理。例如：假设小车当前以较慢的速度在给定路径左边较远的地方行驶，根据前面总结的控制策略，则可控制小车以较大的舵机转角右转，用if-then条件语句表达为：IFE=NB ANDV=VS THENU=PB；表1是该前轮转向控制系统的模糊控制规则表。

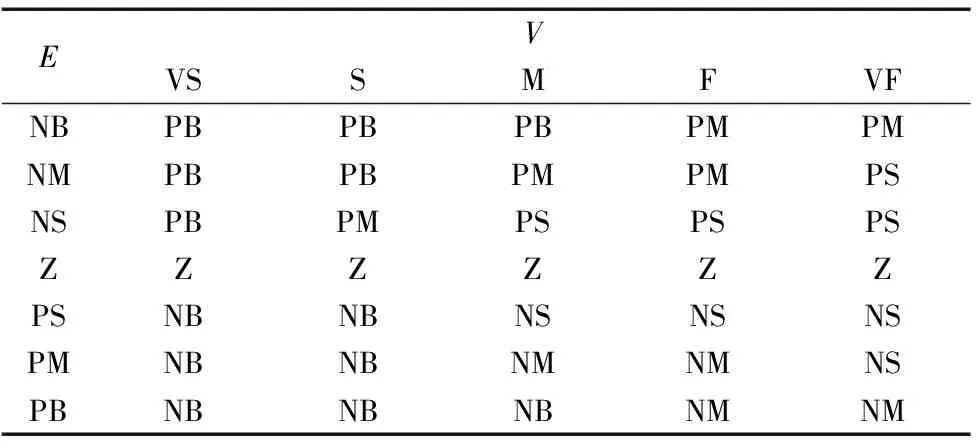
表1 前轮转角U模糊规则表

(3)解模糊，确定模糊清晰化方法

目前模糊量的清晰化方法有很多，较常用的有最大隶属度法、取中位数法和加权平均法(重心法)[8]。鉴于重心法能够全面考虑各输入信号的微小变化，且具有较平滑的输出，此处选用重心法作为解模糊方法。

如图5所示是前轮转向模糊控制器对应的输入输出曲面观测图，它可以直观地反映与整个输入区间(偏差E、速度V)相对应的输出区间(前轮转角U)的变化情况。

图5 前轮转向曲面观测图

3.2 速度调节模糊控制器设计

速度调节模糊控制器负责控制磁导引AGV实时根据路况(小车路径跟踪偏差大小及直行或转弯等信息)调节后轮驱动速度，使之与前轮转向控制协调配合，提高AGV路径跟踪精度。因此对于该速度调节模糊控制器，将偏差E和当前舵机转角φ作为输入，速度UV作为输出。且将输入量E和φ模糊语言变量均定义为：{“负大”，“负中”，“负小”，“零”，“正小”，“正中”，“正大”}={“NB”，“NM”，“NS”，“Z”，“PS”，“PM”，“PB”}，论域为：{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；输出量UV模糊语言变量定义为：{“很慢”，“慢”，“中速”，“快”，“很快”}={“VS”，“S”，“M”，“F”，“VF” }，论域表示为：{0,1,2,3,4,5}；隶属度函数选择及解模糊方法与前轮转向模糊控制器相同，此处不再赘述。根据实际经验，同时考虑到前轮转向舵机在转向角度及响应速度上受到一定的限制，因此在制定速度调节模糊控制规则时可从以下几点着手：①当小车转角值较大时，应适当减慢速度；反之，小车转角值较小时，应适当加快速度；保证前轮转向精度。②当偏差较大时，应减慢小车速度；反之，偏差较小时，可适当加快速度；防止由于惯性影响使小车偏差再次加大。③当小车当前转向与纠偏方向相反时，应适当减慢速度；反之，可适当加快速度。按照此控制思路结合小车实际行驶情况(偏差E<0时，小车相对于给定路径左偏；转角φ<0时，小车左转)，表2列出了对应的速度调节模糊控制规则表。

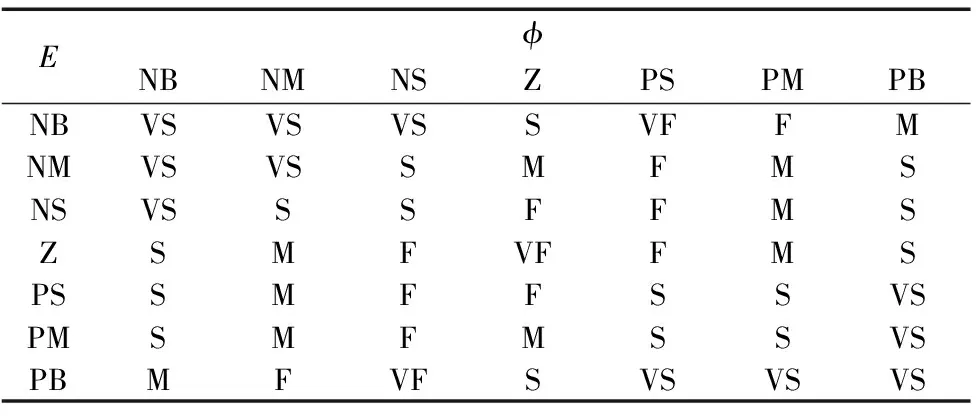
表2 速度调节模糊规则表

图6是速度调节模糊控制器对应的输入输出曲面观测图，它直观地反映了与整个输入区间(偏差E、前轮转角F)相对应的输出区间(小车速度UV)的变化情况。

图6 速度调节曲面观测图

4 仿真分析与验证

为了较直观地反映在上述控制策略下磁导引AGV路径跟踪情况，本文在Matlab中利用其编程功能及图形用户界面(GUI)模块建立了一条带连续转弯的封闭轨道进行路径跟踪仿真实验，实验过程中通过多次仿真修改，最终结果如下：

(1)在后轮速度恒定情况下，对前轮转向控制分别采用传统PID控制和模糊控制算法进行仿真分析与比较。如图7所示是小车在恒定速度(v=0.4m/s)行驶时，前轮转向PID控制与模糊控制轨迹跟踪图；由图7可以看出，在后轮驱动速度保持不变时，前轮转向采用模糊控制比用PID控制整体路径跟踪精度要高、系统鲁棒性要好，尤其是连续转弯时表现比较明显，PID控制转弯时调整时间比模糊控制长。

(a)PID控制轨迹跟踪图 (b)模糊控制轨迹跟踪图图7 恒定低速(v=0.4m/s)轨迹跟踪图

(2)为了体现后轮驱动速度对AGV路径跟踪精度的影响，分别在高速和低速下采用模糊控制对其轨迹跟踪情况进行仿真。如图8所示是小车在恒定高速(v=1.2m/s)行驶时，采用模糊控制轨迹跟踪图；由图7 b和图8可以看出，在采用同样控制算法的情况下，AGV行驶速度快慢对其路径跟踪精度是有影响的，尤其是转弯时，速度越快跟踪精度越低。这也验证了本文控制策略的合理性，即对前轮舵机转向、后轮速度驱动型磁导引AGV应该实时根据路况对其后轮驱动速度进行调节。

图8 恒定高速(v=1.2m/s)轨迹跟踪图

(3)在前轮舵机转向模糊控制和后轮速度调节模糊控制共同协调配合下，AGV轨迹跟踪情况如图9所示。比较图8和图9可以看出：同样采用模糊控制算法，图9 AGV根据路况不断调整速度获得的轨迹跟踪精度和系统鲁棒性较佳，从而验证了本文控制策略的可行性和有效性。

图9 根据路况实时调速时轨迹跟踪图

5 结论

本文重点针对前轮舵机转向、后轮速度驱动型磁导引AGV制定了以模糊控制为主的可实时根据路况合理调整舵机转角和驱动电机速度的路径跟踪控制策略，并通过仿真验证了其可行性，从而为此类驱动方式的磁导引AGV路径跟踪控制提供了一定的理论参考价值。然而模糊控制更多依靠的是人的经验总结，带有主观性，AGV在实际行驶中控制效果可能达不到最优。因此，在后续研究中可尝试采用多种控制算法组合的方式，取长补短进行改进，以求达到最优控制效果。