6自由度超精密线性定位系统误差检测与补偿方法*

李文杰

(西安航空职业技术学院 航空材料工程学院，西安 710089)

0 引言

线性平台的定位性能在精密工业领域(如生物技术、半导体技术和医用光学)方面具有重要作用[1-2]。近年来，随着光学和电子等技术的快速发展，对其精密线性系统的定位精度要求也逐渐提高[3]。定位精度受多种因素影响，大体可以分为几何误差、热诱导误差源、切削力诱导误差源及其它误差源等。

为实现超精密定位，需要消除这些误差源产生的不精确性。从自由度角度分析误差源可以得到6个自由度相关的误差，分别是3个平移误差和3个旋转误差。通常可以通过离线法对定位误差进行测量，以提高定位平台的定位精度。近年来已有相关研究学者对不同自由度线性平台误差源进行研究，并应用各种测量设备测量线性平台的不同自由度相关误差[4-5]。但是，设备性能很大程度上影响了测量结果的准确性。因此，误差测量过程中需要利用最佳传感器以提高测量精度。双球杆可以用来研究几何误差的影响，但是该方法无法分辨出误差的具体类型，同时球杆的分辨率也比其他测量系统的分辨率低[6]；激光干涉仪测量几何误差最精确，但是可适用性较差、耗时长[7]。

另一方面，目前已有的研究所提出的精密定位平台都是针对微位移范围内提高运动定位精度。因此，对于较大行程的线性平台位移运动难以实现误差补偿。同时，已有的相关研究需要对外部测量系统的定位和旋转运动进行控制，不同纳米定位系统的结构或测量系统会对不同自由度误差补偿产生限制[8-9]。并且，之前的研究主要集中在特定误差源产生误差的测量与补偿方面，例如几何误差和热诱导误差等主要误差源。但是，这些离线补偿方法在最小化几何误差时是有用的，由于其时变误差源的特点故不适合用于热诱导误差或动态误差。

基于以上研究，本文提出一种6自由度超精密线性定位系统，并对该精密定位系统几何误差、热诱导误差以及动态误差进行测量并实时补偿。该系统采用刚度高、响应速度快的并联柔性铰链机构，通过对该定位平台动力学进行分析，针对提高定位系统性能提出递归补偿算法；最后对比误差补偿前后的实验结果，分析均方根误差和峰谷值误差，用来验证该装置的有效性。

1 6自由度超精密定位平台的设计

1.1 系统设计

线性平台能够提供大的工作空间和快速的加速度。本文所提出的6自由度超精密定位系统安装在线性平台上，其原理如图1所示。通过压电驱动器对多自由度柔性机构进行驱动可以实现较高分辨率。线性系统坐标系与末端执行器坐标系之间关系恒定，与机床指令无关，见下式：

(1)

6自由度超精密定位平台装置如图2所示。驱动组件包括基准平台、移动平台、6个压电驱动器以及6个柔性关节。压电驱动器位于基准平台和移动平台之间。由于并联机构的特点，驱动元件结构刚性强，响应速度快。两自由度关节与移动平台项相连，3自由度关节与基准平台相连。因此，驱动组件可以实现6自由度运动(三平移三旋转)。5个电容式传感器和参考镜作为测量工具测量几何误差、热误差以及动力学误差。传感器采集的数据用于对精密平台5自由度误差进行补偿(两平移误差和三旋转误差)。补偿算法和旋转运动驱动工作台保持最终的目标位置。

图1 微纳定位平台原理

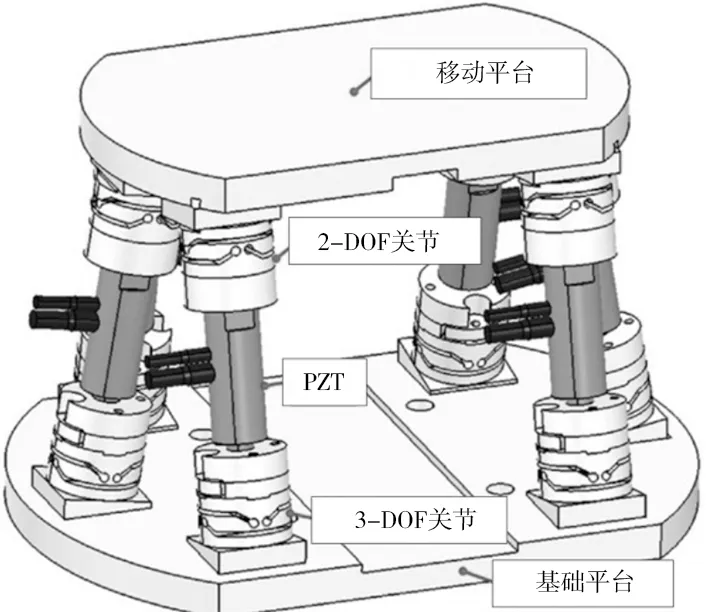
图2 6自由度超精密定位系统结构图

1.2 动力学分析

测量和驱动坐标系统用于识别运动平台的中心和定义参考坐标系，通过Abbe误差的最小化实现对误差的精确测量和补偿。用逆运动学方法计算补偿特定误差所需要的压电驱动器位移Δli(i=1,2,3)，运动平台{M}、基准平台{B}以及关节{i},{j}的坐标系统定义如图3所示。

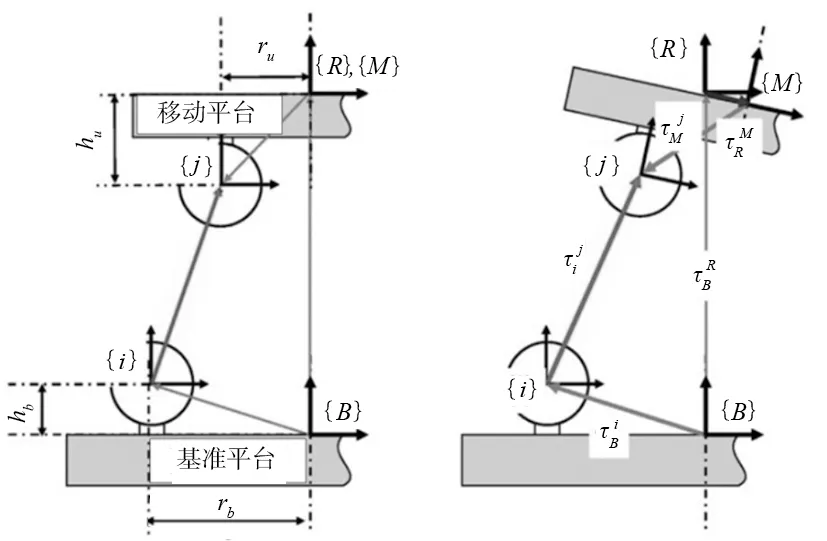
图3 动力学反解坐标系统

参数hb和rb分别表示基准平台{B}和关节{i}关于基准平台上的高度和半径。同样地，参数hu和ru分别表示相对坐标系统{M}和关节坐标系统{j}关于移动平台上的高度和半径。其中关节坐标系统{i}和{j}通过运动链进行确定，见式(2)。利用齐次变换矩阵对系统刚性部分的运动进行建模，其中R和P分别表示关节坐标系{i}相对于{j}的旋转矩阵和位移矢量。

(2)

式(2)中具体参数计算如下：

P=(xyz)T

(3)

并联机构受工作空间大小的限制，柔性关节的使用大大降低了工作空间的大小。因此，工作空间分析要求运动可行性验证，利用正向运动学方法计算了动平台的位姿和压电陶瓷的位移。定义两个平台坐标系统中每个关节的速度为ai,bi(i=1,2,...,6)，计算压电驱动器的位移，表示为di(i=1,2,...,6)。采用高斯-牛顿方法，结合式(4)和式(5)计算位移与6自由度误差之间的关系。其中，压电驱动器范围为±7.5mm。

(4)

(5)

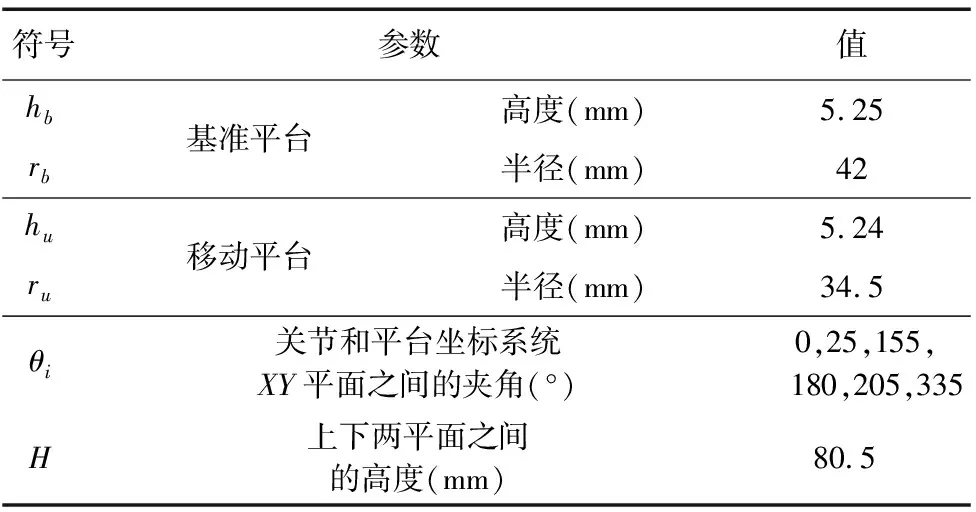
表1 纳米定位平台设计参数

2 误差测量及补偿

如图4所示，利用参考平面镜和5个电容式传感器对线性平台5自由度误差进行测量。在运动参考镜和5个电容式传感器条件下，位置误差的标准不确定性显著增加。因此，使固定在传感器位置上的末端执行器沿轴向移动，并根据传感器测得的数据估计几何误差。参考坐标系统用来定义测量和驱动坐标系识别移动平台的中心和传感器的位置si(i=1,2,...,5)。参数l,h和w分别表示传感器距离、高度以及宽度。利用式(6)计算测量数据mi(i=1,2,...,5)，其中下标表示不同传感器编号：

(6)

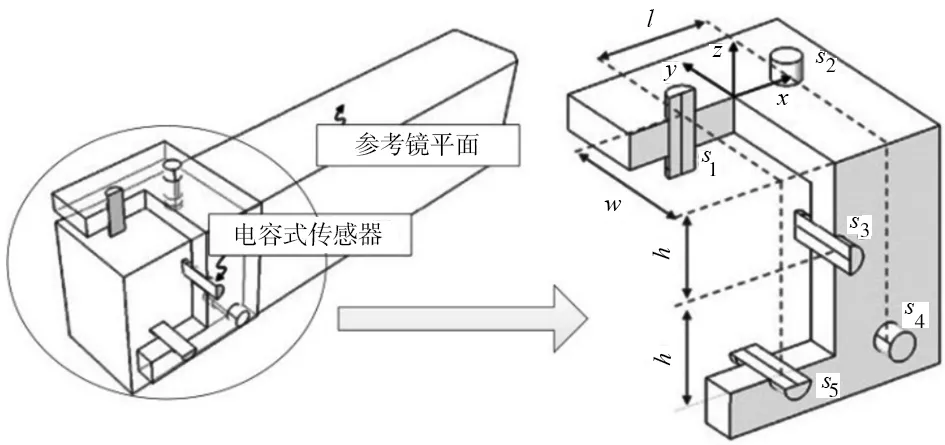
图4 误差测量装置

测量数据的标准不确定度直接受到基准面平面度和传感器性能(线性度和分辨率)等不确定因素的影响。因此，为了评价测量结果的可靠性，对测量设备的不确定度因素进行了分析，并计算测量数据的标准不确定度。用测量数据的标准不确定度评定了5自由度误差的标准不确定度。本文通过设置传感器与参考坐标系之间的最佳关系，测量出5自由度误差的标准不确定度。

利用传感器si(i=1,2,...,5)得到的数据计算5自由度误差和各传感器数据与几何误差的关系，见式(7)。因此，可以对驱动轴{X}上两位置误差(水平直线度误差δyx和垂直直线度误差δzx)和三转动误差(旋转误差εxx、俯仰εyx和偏转误差εzx)进行计算。估计误差可用于逆运动学建模和压电驱动器位移Δli计算。因此，6自由度定位机构中运动平台沿固定参考镜的恒定姿态直线进行运动。

(7)

除了前面所讨论的误差外，双伺服系统的制造误差和装配误差也影响到直线轴的精度。为此提出误差补偿算法进行补偿以提高定位精度。理想坐标系统{X}i应遵循参考坐标系{R}的x轴，但是实际坐标系统{X}a会发生偏离。位置μ包括6自由度运动(三平移和三旋转运动)，本文中由于系统可以对线性平台5自由度误差进行测量，所以μ表示两平移和三旋转运动，如式(8)所示：

μ=(δxxδyxδzxεxxεyxεzx)T

(8)

补偿的过程就是使实际位置的坐标系统{X}a应与理想坐标系统{X}i重合，但由于双伺服系统的制造和装配误差，以及几何、热感应和动态误差等时变误差，使得两个坐标系的匹配变得复杂。因此，采用临界运动Δμi(i=1,2,...,n)进行i次补偿得到补偿后的补偿坐标系{X}ith，见式(9)：

Δμi=(δiεi)T

(9)

式中，δi=(δxx,iδyx,iδzx,i)T，εi=(εxx,iεyx,iεzx,i)T。

进行i次补偿后，μ+∑Δμi对剩余运动Δμi(i=1,2,...,n)进行补偿。当残余运动Δμi(i=1,2,...,n)在公差范围内时，迭代过程就完成了。因此，双伺服系统根据给定的公差控制坐标系对实际坐标系统{X}a进行匹配，具体补偿流程图如图5所示。通过动力学反解计算压电驱动器特定运动位移Δli(i=1,2,...,6)，通过测量的运动来计算的补偿值，以满足公差内的剩余运动Δμi(i=1,2,...,n)，本文中设定公差值为60nm。

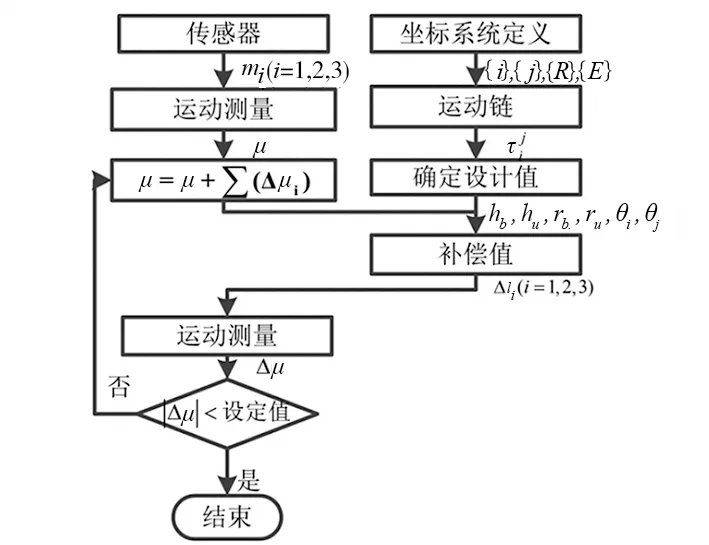
图5 补偿算法流程图

3 实验

为便于获得所需要的关节尺寸，采用高精度电火花线切割加工的方法制备纳米定位平台的柔性关节。其中电容式传感器、压电驱动器和参考平面镜参数如表2所示。由于受参考平面镜大小的限制，整个系统设置为宽100mm、长80mm、高78.5mm。参考镜由微晶玻璃制造，不受热诱导引起的误差影响。驱动器组件安装在线性轴上，固定参考镜以最小化Abbe误差。

用LabVIEW软件对5自由度误差进行实时测量和补偿，补偿算法对压电驱动器位移Δli(i=1,2,...,6)进行计算。用激光干涉仪对电容传感器和参考镜测量结果的有效性进行了验证。当使用激光干涉仪测量定位误差时，必须考虑Abbe误差以进行精确测量。因此，激光干涉仪的测量坐标系与补偿机构末端执行器的基准坐标系相匹配，以尽量减少测量系统之间的Abbe偏移。具体测量结果如图6所示。由图6a和图6b可知，基于6自由度定位系统提出的误差测量系统计算得到的平移误差和旋转误差测量结果与激光干涉仪实际测量结果相吻合，两个测量方法之间的最大差值在数据的可重复性之内。另外，随着定位系统线性轴向位置的增大，旋转误差逐渐减小，表明该系统适用于具有较大行程的定位。因此，验证了实验中所使用的测量系统有效性。平移运动的峰谷误差值为2.17μm，转动误差为8.22rad/s。

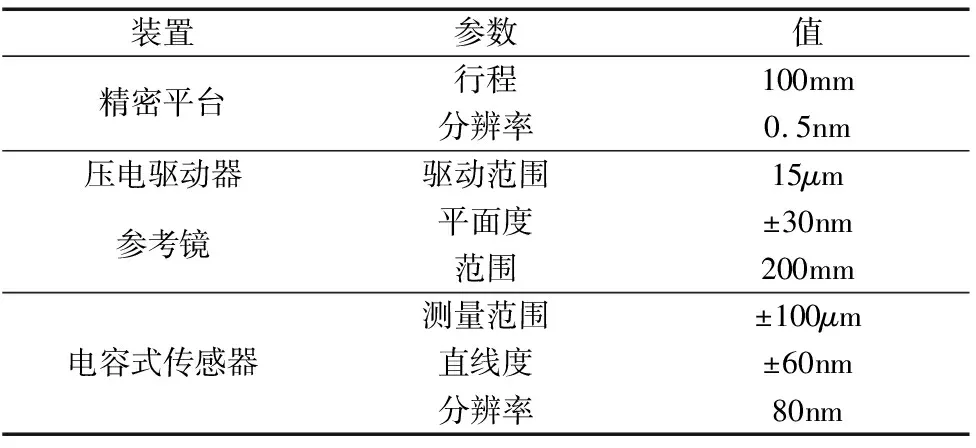
表2 实验装置参数

(a)平移误差

(b)旋转误差图6 误差测量系统验证对比实验

精密平台的5自由度误差补偿前后对比结果如表3所示。在实验结果中，补偿后位置误差和旋转误差的PV值分别降低到7%和5%。位置均方根误差和旋转均方根误差分别减少了91%和96%。动态条件下的实验结果与稳态结果相比有增加的趋势。然而，RMSE和PV在理论的公差范围(±0.2弧秒的旋转运动和±50 nm的位置运动)。因此，验证了本文提出的误差补偿算法的有效性。

表3 误差补偿结果

4 结论

本文提出一种6自由度线性超精密定位系统。该系统可以实现期望的线性定位同时能够对几何误差、热诱导误差和动态误差引起的6自由度误差进行实时补偿。补偿机制采用柔性铰链来获得超精密定位，同时采用联机构，具有结构刚度高、响应速度快等特点。通过对工作台的运动学进行动力学分析，提出基于递归技术的补偿算法，提高了系统的定位精度，并通过实验验证了测量系统和补偿算法的有效性。