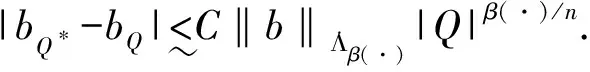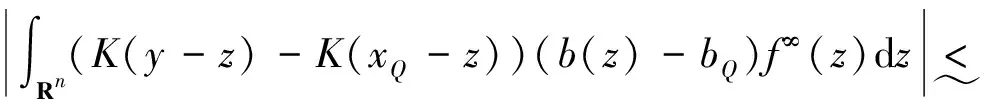变指数Lipschitz交换子在变指数空间上的有界性
郭庆栋,周 疆,房成龙
(新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)
1 预备知识



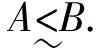
的可测函数组成的集合定义为P (Rn).
定义1.1[3](ⅰ) 设ɡ是连续函数,若存在clog>0使得对所有的x,y∈Rn,满足




定义1.3[5]若p:Rn→(0,∞)是可测函数,Lp(·)(Rn)表示下面函数的集合:
其范数定义为


此外,记B (Rn)为所有满足p(·)∈P (Rn)且Hardy-Littlewood极大算子在Lp(·)(Rn)上有界的函数组成的集合.
同时,为了后面定理的证明更加简洁,定义算子Mδ及变指数分数次极大算子Mα(·)如下:
定义1.5[5]设K是定义在Rn{0}上的局部可积函数,K的Fourier变换的支集是有界的,且K满足
(1)
则对应的奇异积分算子T定义为Tf(x)=K*f(x).若p(·)∈B (Rn),则T在Lp(·)(Rn)上是有界的.

[b,T]f(x)=b(x)Tf(x)-T(bf)(x).
定义1.6[5]设0<α 进一步,若1/p(·)-1/q(·)=α/n,则Iα从Lp(·)(Rn)到Lq(·)(Rn)是有界的.[6] [b,Iα]f(x)=b(x)Iαf(x)-Iα(bf)(x). 另外,变指数Riesz位势算子Iα(·)定义如下: 上面估计中,Mβ(·)f(x)≤CIβ(·)(|f|)(x)[8],根据引理2.1即可得定理结论. 证明根据引理2.1, 定理2.3设β(·)∈Clog(Rn),q(·)∈P0(Rn),p(·)∈B (Rn),1/p(·)-1/q(·)=α/n,1/p(·)-1/r(·)=(α+β(·))/n.若 由此可得 根据引理2.1,变指数分数次积分算子Iα+β(·)(|f|)从Lp(·)到Lr(·)是有界的,定理得证. 引理3.1[4]若β(·)∈P0(Rn),q(·)∈P (Rn),则 容易验证 [b,T]f=[b-bQ,T]f,故 首先估计D1. 其次估计D2.取1/p(·)-1/q(·)=β(·)/n,根据[b,T]从Lp(·)到Lq(·)的有界性,可得 则有 定理3.2设β(·)∈Clog(Rn)∩P0(Rn),q(·)∈P (Rn),p(·)∈B (Rn)且满足 证明容易验证,[b,Iα]f=[b-bQ,Iα]f,故 首先估计E1. 其次估计E2.取 1/p(·)-1/r(·)=(α+β(·))/n, 根据[b,Iα]从Lp(·)到Lr(·)的有界性,可得 最后估计E3. 故

2 变指数Lebesgue空间上交换子的有界性


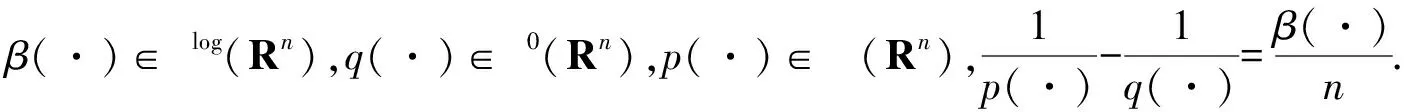



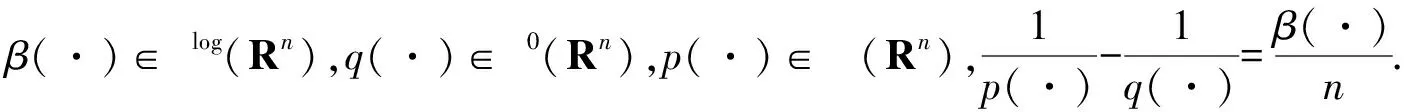

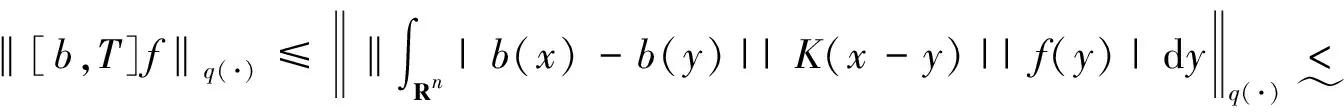


3 变指数Lipschitz空间上的有界性