Lie-Yamaguti超代数的交换扩张

唐鑫鑫，胡梦如，徐建国，张庆成

(1.东北师范大学数学与统计学院，吉林 长春130024；2.通化师范学院数学系，吉林 通化 134000)

1 预备知识

Lie-Yamaguti代数最初由Yamaguti[1]提出，相关研究可参考文献[2-9].Lie-Yamaguti超代数是Lie-Yamaguti代数的推广.本文将研究Lie-Yamaguti超代数的交换扩张，证明了交换扩张可由(2，3)-上同调群分类，推广了文献[8]中的结论.

定义1Lie-Yamaguti超代数是一个三元组(A，[-，-]，{-，-，-}).其中：A是一个超空间；[-，-]：A×A←A是一个偶双线性映射；{-，-，-}：A×A×A→A是一个偶三重线性映射.其满足：

(LYS1) [x1，x2]+(-1)|x1||x2|[x2，x1]=0；

(LYS2) [x1，x2，x3]+(-1)|x1||x2|[x2，x1，x3]=0；

(LYS5) {x1，x2，[y1，y2]}=[{x1，x2，y1}，y2]+(-1)|y1|(|x1|+|x2|)[y1，{x1，x2，y2}]；

(LYS6) {x1，x2，{y1，y2，y3}}={{x1，x2，y1}，y2，y3}+(-1)|y1|(|x1|+|x2|){y1，{x1，x2，x3}，y2}+(-1)(|x1|+|x2|)(|y1|+|y2|){y1，y2，{x1，x2，y3}}；

(LYS01) |[x1，x2]|=|x1|+|x2|；

(LYS02) |{x1，x2，x3}|=|x1|+|x2|+|x3|.

定义2设(A，[-，-]1，{-，-，-}1)和(A2，[-，-]2，{-，-，-}2)是Lie-Yamaguti超代数.A1和A2之间的同态是指一个偶线性映射φ：A1→A2，满足：

φ([x1，x2]1)=[φ(x1)，φ(x2)]2，φ({x1，x2，x3}1)={φ(x1)，φ(x2)，φ(x3)}2.

定义3设A是Lie-Yamaguti超代数，V是一个超空间.A在V上的表示是一个三元组(ρ，γ，θ)，这里ρ：A→End(V)是一个线性映射，γ，θ：A×A→End(V)是双线性映射，满足：

(SR1)γ(x1，x2)-(-1)|x1||x2|θ(x2，x1)+θ(x1，x2)+ρ([x1，x2])-ρ(x1)ρ(x2)+(-1)|x1|x2|，ρ(x2)ρ(x1)=0；

(SR2) (-1)|x1||x3|γ([x1，x2]，x3)+(-1)|x1||x2|γ([x2，x3]，x1)+(-1)|x2||x3|γ([x3，x1]，x2)=0；

(SR3)θ([x1，x2]，y1)=(-1)|x2||y1|θ(x1，y1)ρ(x2)-(-1)|x1|(|x2|+|y1|)θ(x2，y1)(ρ(x1)；

(SR4)γ(x1，x2)ρ(y2)=(-1)|y2|(|x1|+|x2|)ρ(y2)γ(x1，x2)+ρ({x1，x2，y2})；

(SR5)γ(x1，x2)θ(y1，y2)=(-1)(|x1|+|x2|)(|y1|+|y2|)θ(y1，y2)γ(x1，x2)+θ({x1，x2，y1}，y2)+(-1)|y1|(|x1|+|x2|)θ(y1，{x1，x2，y2})；

(SR6)θ(x1，{y1，y2，y3})=(-1)(|x1|+|y1|)(|y2|+|y3|)lθ(y2，y3)θ(x1，y1)-(-1)|x1||y1|+|y2||y3|+|x1||y3|θ(y1，y3)θ(x1，y2)+(-1)|x1|(|y1|+|y2|)γ(y1，y2)θ(x1，y3).

V也称为一个A-模.

设映射ν：A×A→V满足ν(x1，x2)=-(-1)|x1||x2|ν(x2，x1)，映射ω：A×A×A→V满足ω(x1，x2，x3)=-(-1)|x1||x2|ω(x2，x1，x3).由ν生成的空间记为C2(A，V)，由ω生成的空间记为C3(A，V).

定义4设A是Lie-Yamaguti超代数，V是A-模.(ν，ω)∈C2(A，V)×C3(A，V)称为(2，3)-闭上链算子，若其满足：

(CC3)ω(x1，x2，[y1，y2])+γ(x1，x2)ν(y1，y2)=ν({x1，x2，y1}，y2)+(-1)|y1(|x1|+|x2|)ν(y1，{x1，x2，y2})+(-1)|y1|(|x1|+|x2|)ρ(y1)ω(x1，x2，y2)-(-1)|y2|(|x1|+|x2|+|y1|)ρ(y2)ω(x1，x2，y1)；

(CC4)ω(x1，x2，{y1，y2，y3})+γ(x1，x2)ω({y1，y2，y3})=ω({x1，x2，y1}，y2，y3)+(-1)|y1|(|x1|+|x2|)ω(y1，{x1，x2，y2}，y3)+(-1)(|x1|+|x2|)(|y1|+|y2|)ω(y1，y2，{x1，x2，y3})+(-1)(|y2|+|y3|)(|x1|+|x2|+|y1|)θ(y2，y3)ω(x1，x2，y1)-(-1)(|x1|+|x2|)(|y1|+|y3|)+|y2||y3|θ(y1，y3)ω(x1，x2，y2)+(-1)(|x1|+|x2|))|y1|+|y2|)γ(y1，y2)ω(x1，x2，y3).

由(2，3)-闭上链算子生成的空间记为Z2(A，V)×Z3(A，V).

定义5设A是Lie-Yamaguti超代数，V是A-模.(ν，ω)∈C2(A，V)×C3(A，V)称为(2，3)-上边缘算子，若存在映射f：A→V满足：

(BB1)ν(x1，x2)=ρ(x1)f(x2)-(-1)|x1||x2|ρ(x2)f(x1)-f([x1，x2])；

(BB2)ω(x1，x2，x3)=(-1)|x1|(|x2|+|x3|)θ(x2，x3)f(x1)-(-1)|x2||x3|θ(x1，x3)f(x2)+γ(x1，x2)f(x3)-f({x1，x2，x3}).

由(2，3)-上边缘算子生成的空间记为B2(A，V)×B3(A，V).

命题1B2(A，V)×B3(A，V)⊆Z2(A，V)×Z3(A，V).

定义6Lie-Yamaguti超代数A的取值在V中的(2，3)-上同调群定义为商空间

H2(A，V)×H3(A，V)∶=(Z2(A，V)×Z3(A，V))/(B2(A，V)×B3(A，V)).

2 交换扩张

通过证明交换扩张由(2，3)-上同调群分类，建立Ext(A，V)和H2(A，V)×H3(A，V)之间的一一对应.

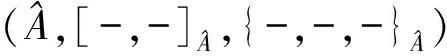
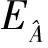
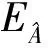
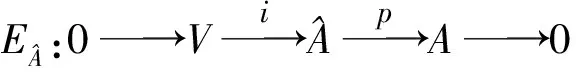
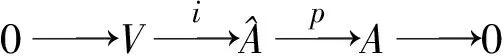
A通过V的交换扩张的等价类集合记为Ext(A，V).

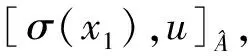
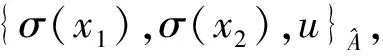
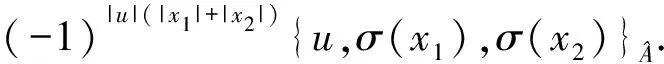
则(ρ，γ，θ)是A在V上的一个表示，且与sectionσ的选择无关.此外，等价的交换扩张给出相同的表示.

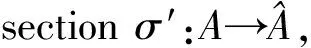
ρ(σ′(xi)-σ(xi))=xi-xi=0，

从而

σ′(xi)-σ(xi)∈V⟹σ′(xi)=σ(xi)+ui，对某个ui∈V.

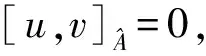
故ρ与σ的选择无关.类似可证明γ，θ与σ的选择无关.

可得条件(SR31)成立.

因此，等价的交换扩张给出相同的θ.类似可证明等价的交换扩张给出相同的γ和ρ.

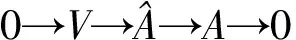
则(ν，ω)是A的取值在V中的(2，3)-闭上链.

证明首先证明ν的像包含在V中，即p∘ν(x1，x2)=0.因为p是一个代数同态，故

p∘ν(x1，x2)=[p∘σ(x1)，p∘σ(x2)]-p∘σ([x1，x2])=[x1，x2]-[x1，x2]=0.

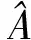
从而

x1，x2，x3(-1)|x1||x3|ω(x1，x2，x3)+x1，x2，x3(-1)|x1||x3|σ({x1，x2，x3})+
x1，x2，x3(-1)|x1||x3|ν([x1，x2]，x3)+
x1，x2，x3(-1)|x1||x3|σ([[x1，x2]，x3])=0.

于是条件(CC1)成立.

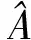
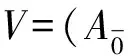
[x1+u1，x2+u2]ν=[x1，x2]+ν(x1，x2)+ρ(x1)(u2)-(-1)|x1||x2|ρ(x2)(u1)，

{x1+u1，x2+u2，x3+u3}ω={x1，x2，x3}+ω(x1，x2，x3)+γ(x1，x2)(u3)-
(-1)|x2||x3|θ(x1，x3)(u2)+(-1)|x1|(|x2|+|x3|)θ(x2，x3)(u1).

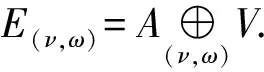
证明只需证明条件(LYS1)—(LYS6)在A⨁V上仍然成立.

等式(LYS1)改写为

[x1+u1，x2+u2]ν+(-1)|x1||x2|[x2，u2，x1+u1]ν=0.

直接计算得

[x1+u1，x2+u2]ν+(-1)|x1||x2|[x2+u2，x1+u1]=
[x1，x2]+ν(x1，x2)+ρ(x1)(u2)-(-1)|x1||x2|ρ(x2)(u1)+
(-1)|x1||x2|[x2，x1]+(-1)|x1||x2|ν(x2，x1)+(-1)|x1||x2|ρ(x2)(u1)-ρ(x1)(u2)=0.

故条件(LYS1)成立.

同理可证明(LYS2)—(LYS6)在A⨁V上成立.

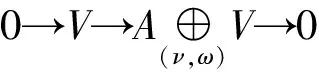
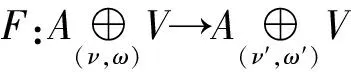
F[x1+u1，x2+u2]ν=[F(x1+u1)，F(x2+u2)]ν′，

(1)

F{x1+u1，x2+u2，x3+u3}ω={F(x1+u1)，F(x2+u2)，F(x3+u3)}ω′.

(2)

因为F是扩张的等价，故存在f：A→V使得

F(xi+u)=xi+f(xi)+u，xi∈A.

故(1)式等价于

f([x1，x2])+ν(x1，x2)=ν′(x1，x2)+ρ(x1)f(x2)-(-1)|x1||x2|ρ(x2)f(x1)，

即

(ν-ν′)(x1，x2)=ρ(x1)f(x2)-(-1)|x1||x2|ρ(x2)f(x1)-f([x1，x2]).

(2)式等价于

f({x1，x2，x3})+ω(x1，x2，x3)=ω′(x1，x2，x3)+γ(x1，x2)f(x3)-
(-1)|x2||x3|θ(x1，x3)f(x2)+(-1)|x1|(|x2|+|x3|)θ(x1，x3)f(x1)，

进而

(ω-ω′)(x1，x2，x3)=γ(x1，x2)f(x3)-(-1)|x2||x3|θ(x1，x3)f(x2)+
(-1)|x1|(|x2|+|x3|)θ(x2，x3)f(x1)-f({x1，x2，x3}).

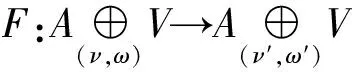
定理1设A是Lie-Yamaguti超代数，V是一个A-模，则

Ext(A，V)≅H2(A，V)×H3(A，V).

因此A通过V的交换扩张由(2，3)-上同调群分类.