倒置液滴法的非球面微小透镜制作及实验研究

王松子，简伟明，王 翔

（中国科学技术大学精密机械与精密仪器系，安徽合肥230026）

1 引 言

微透镜及其阵列在众多应用光学领域有着广泛的应用，而非球面微透镜能够有效地减小像差和光能损失，提高成像质量，可以有效地简化光学系统的结构。在红外光学系统中非球面的应用可有效弥补透过红外波段材料少而产生象差校正特别是色差校正困难的不足［1］；在面向医学医疗与工业检测领域的热成像系统，以及激光束整形等，非球面透镜有利于红外透镜设计到衍射极限，有效地解决复杂的光束整型和宽波段范围内的消色差，并能使得光学系统更小和更轻［2-3］。为此，可实现面形有效调控的制造方法就成为了非球面微透镜及其阵列研究的热点之一［4-5］。目前，非球面微透镜的制造方法主要包括飞秒激光双光子聚合加工［6］，注塑成型［7］，玻璃模压成型［8］以及单点金刚石数控车削［9］等，但是，相关的方法存在着制造效率低、模具要求高且易产生气泡裂纹，以及装备和工艺复杂等诸多有待进一步完善的问题。

对于直接制造聚合物微小透镜的热熔融法［10］和液滴法［11］，具有无需模具、流程简单、成本低廉等优点，在球面微透镜及其阵列的制造中已得到了广泛的研究和应用。

对于液滴法来说，其基本成形原理是利用微小液滴在表面张力作用下，在固体上铺展形成球冠的现象来获得平凸形、表面光洁微透镜及阵列；在其成形过程中，通常因其体积较小而忽略体积力（重力）的影响，其形貌主要由表面张力作用而呈现为球面面形。

但是，当液滴体积较大时，实际成形过程中，体积力对液滴稳态面形的形状有着直接的影响，且体积力与表面张力的作用的合力方向不同，将使液滴形貌呈现为不同的非球面趋势。为此，本文利用流体动力学的基本原理，通过对正置于固体基底和倒置于固体基底上的液滴形貌演变的考察，将垂悬液滴引入到非球面透镜制作中，通过不同体积力对液滴的稳态非球面形貌的影响分析，结合紫外光固化技术来制作非球面微透镜，并通过对非球面面形与光学性能的测量，来实现不同面形非球面微透镜的制作。

2 倒置液滴法制作非球面微小透镜的原理方法

2.1 水平固体基底上液滴的面形演化趋势

放置在固体基底上的液滴，在表面张力作用下将在固体表面铺展为球冠形，如图1（a）所示。当面形稳定时，其在液、固、气三相交界处满足式（1）所示的 Young方程［12］：

其中，θ为液滴与固体基底的接触角；γSL为固-液表面张力系数；γSG为固-气表面张力系数；γLG为液-气表面张力系数。

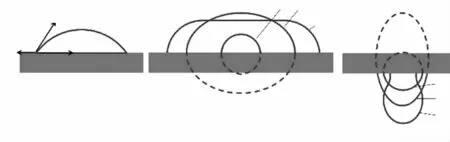
图1 固体基底上液滴的面形演化趋势Fig.1 The evolving process of the profile of the droplet on a solid substrate

固体基底上液滴的形貌除了受到表面张力作用影响之外，还受到自身体积力（重力）的作用。表面张力使得液滴形状呈现为球形，而重力则使得液滴呈现非球面化，且体积越大，重力作用越明显，液滴的面形也将越偏离球面。如图1（b），正置液滴在重力作用下，面形将随体积增大由球面变为扁平的非球面（由轮廓1→轮廓2），甚至变为顶部水平两端圆弧的面形（轮廓3）。而对于倒置液滴，如图1（c）所示，在重力作用下，体积小可忽略时仍呈现为球形（轮廓1），随着体积增大，面形向凸形的非球面方向发展（轮廓2），当体积继续增大将会出现类似滴珠而滴落（如轮廓3）。

通常描述透镜面形轮廓的二次曲面可如式（2）所示［13］：

其中，r，z分别为径向坐标和矢高方向坐标；R为顶点曲率半径；K为非球面系数。

按K值不同可将二次曲面分为扁椭球面（K＞0）、球面（K=0）、凸椭球面（-1 ＜K＜0）、抛物面（K=-1）和双曲面（K＜-1）。

为此，利用倒置的垂悬液滴可以通过选取合适的体积，来得到有利于减小球差的非球面系数小于零的微小透镜。

2.2 两相流模型求解液滴的面形演化

对于在固体基底上的液滴，其面形演化属于液、气两相流问题，利用COMSOL的层流两相流模块（Laminar Two-Phase Flow，Moving Mesh Interface）可以建立两个互不混溶的层流体流动模型，结合移动网格技术应用，可以跟踪流体界面的位置变化。

通常用于高分子材料作为直接制作微透镜的材料—光固胶，可认为是不可压缩的牛顿流体，根据动量守恒定律，液滴流体满足Navier-Stokes方程［14］：

其中，ρ是流体的密度；u是液滴内部各点的速度矢量；g是重力加速度；P是流体各点的压强；μ是流体的动力学粘度。

液滴流体的流动除了服从N-S方程外，其还满足质量守恒定律，服从连续性方程：

N-S方程和连续性方程是表述液滴流动的微分方程，求解这两个偏微分方程，可以了解对液滴内部在表面张力和体积力共同作用下的压力分布，以及液滴的流动情况，进而得到不同情况液滴相对稳态下的面形。

为了求解固体基底上的轴对称液滴的变化，如图2所示设置求解域及边界条件，设置液滴矢高方向为对称轴（Z轴），液滴与固体基底接触底边为径向轴（r轴），而液滴与空气的交界面（即液滴形貌轮廓）定义为边界2，并在固-液-气三相接触点3处设置液滴与基底的接触角，且假设此接触角在液滴变形过程中始终保持为恒定值；为此，即可将由Z轴、r轴和液滴轮廓2所包围的可自由变形的液滴流体（区域1）作为求解的物理解区域；并假设其初始形状为液滴不受体积力影响时在对应接触角下形成的球冠形状；其后在区域1内添加体积力，其方向为负表示为正置于固体基底上方的固着液滴，体积力方向为正时，可以用来计算悬垂液滴的形貌变化。

图2 液滴两相流计算几何模型Fig.2 The geometry model of the two-phase flow model

图3 （a）（b）分别为体积 V=1 μL和 V=10 μL的正置液滴的面形演化过程，其中图I为零时刻的速度-压力分布图，图中带箭头细实线表示液滴流动的速度与方向，（线段长度表示速度的大小），等压线图总体显示为不均匀的同心圆状分布（图例的压力标尺数值不同，是因为弯曲液面带来的附加压力，液面曲率半径越小其附加压力越大［15］，故图3（a）的小体积液滴内部压力显示大于大体积液滴图3（b）的内部压力）。气液界面处压力较小，液滴内部压力较大，且在对称轴原点处压力最大，故液体将由对称轴向三相接触线方向流动，且小体积液滴（图3（a-I）相比较大体积力作用图（3（b-I），表现出较小的流动速度；液滴矢高减小，顶点曲率半径与底径将增大，且在t=0.5 s时取得相对稳态（图3II）稳态时，等压线也演化为相对均匀的层状分布。

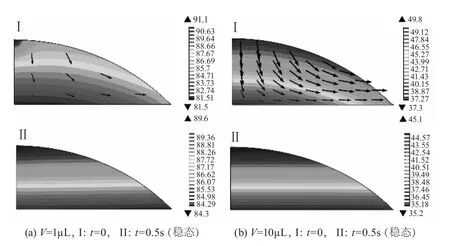
图3 不同体积正置液滴面形变化的速度-压力分布Fig.3 The distributions of velocity and pressure of sessile droplets at different volumes

利用MATLAB分别对图3（a）（b）所示液滴稳态面形轮廓（图II）进行拟合，有：体积V=1μL时面形的非球面系数K=0.24，底径D=2.28 mm，矢高h=0.46 mm，高径比比初始球面面形减小3%；体积V=10μL的图（b）的面形非球面系数 K=1.37，底径D=4.97 mm，矢高 h=0.96 mm，高径比比初始球面面形减小了7%。

由此可知，随着液滴体积的增大，体积力使得液滴向非球面系数K＞0的扁椭球演变，且体积越大非球面系数K也越大，高径比越小，即液滴面形将逐渐坍塌为扁椭球面，甚至变得如图1（b）-3所示的平坦面形。

图4（a）（b）为倒置液滴在表面力和体积力共同作用下的速度-压力分布。其中图4（a）为液滴体积为5μL，从初始时刻至稳态过程的速度-压力分布变化，由图可知，在零时刻的液滴内部等压线分布和气液界面上的速度分布（带箭头细实线）如图4（a-I）所示，压力分布呈现为不均匀的同心圆状分布，在不同高度上，对称轴处的压力较小，气液界面处压力较大；在气液界面上的顶点处为压力较小的奇点，液体将向对称轴和顶点下方流动；图4（a-II）和图4（a-III）分别为 t=0.005 s和 t=0.5 s时对应的速度-压力分布，可见等压线逐渐由同心圆状分布演化为相对均匀的层状分布，且顶点处的压力较高，靠近基底处压力较低。当t=0.5 s时液滴内部速度基本为零，从而得到相对稳定的面形。同时，由图 4（a-I、II、III）中表示液滴气液界面上流动速度大小与方向的带箭头细实线同样可以看出，液滴在对称轴附近液体向下的流速较大，靠近基底部分液体水平流向对称轴方向的流速较小；且在初始时刻图4（a-I）具有较大流速，其后逐渐减小图4（a-II）直至等到稳态图 4（a-III）。

图4 不同体积垂悬液滴面形演化的速度-压力分布Fig.4 A two-phase flow model for liquid drop surface evolution

图4 （b）为体积力较大（V=15 μL）时倒置液滴的从初始时刻至稳态过程变化的速度-压力分布。其速度和压力的变化趋势与图4（a）所示体积为5μL垂悬液滴相同；但是，较大体积液滴（图4（b-I）相对较小体积液滴（图4（a-I）具有较大的流动速度，即表明在相同时间内，体积力较大时（图4（b-I）流动越快，如图 4（b-II）相对图 4（a-II）呈现的流速较小。

同样利用MATLAB分别对图4（a）（b）所示垂悬液滴稳态面形轮廓（图4III）拟合可以得到相应的面形参数：较小体积的图4（a）的非球面系数K=-0.55，底径 D=3.77 mm，矢高 h=0.833 mm；较大体积的图4（b）的非球面系数K=-1.03，底径D=5.40 mm，矢高h=1.25 mm。

由不同体积倒置液滴稳态面形轮廓拟合结果可知，液滴体积力使得液滴向非球面系数K＜0的凸椭球演变，且体积越大非球面系数K也越小，其面形从初始时刻的球面向凸椭球面、抛物面（K=-1），甚至是向双曲面方向拉伸。

3 微小透镜制作实验与结果分析

3.1 实验装置与制作方法

液滴法制作微小透镜实验的主要流程为：基底制备，液滴的按需滴定和紫外光原位固化。基底制备是对基底材料表面的清洗得到具有一定亲水性的表面（使得光固胶液滴在其上具有小于90°的接触角）；不同体积的液滴可利用移液器来实现按需滴定；在液滴形态稳定后，利用紫外光的均匀曝光固化即可得到固态的非球面微透镜。再利用CCD即可得到微小透镜面形轮廓。实验装置如图5所示。

图5 实验装置原理图Fig.5 Schematic diagram of experimental setup

实验所用的紫外光固化胶为台湾德渊公司的1551M2 胶，黏度为 0.45 Pa·s，密度为 1050 kg/m3，表面张力γ=0.032 N/m，折射率n=1.48。具有瞬时固化，固化收缩率小，价格低廉，流动性好等优点。所采用的基底为普通硅酸盐玻璃，对未经固化1551 M2光固胶在其上的接触角，利用θ/2法进行测量，其接触角θ=45°。液滴定量滴定由活塞式单道可调移液器（Dragonlab公司，7855型）完成，其量程范围为0.5～10μL，最小滴定量0.1μL，一致性误差小于2%。

液滴轮廓测量模块由红光LED背光源，连续可调焦物镜（1×～7×）和CCD组成，位于三维移动平台上的液滴轮廓在CCD上清晰成像，经图像采集卡传输给计算机，便可利用MATLAB进行图像处理来得到实际固化后液滴的形貌。

3.2 微小透镜制作与轮廓测量

在利用前文的COMSOL层流两相流模型计算的基础上，选取合适的液滴体积：正置液滴时不出现顶部水平的面形（如图1（b）的轮廓3），倒置时不出现如图1（c）轮廓3所示的类似滴珠的面形。并利用搭建的实验装置来进行不同体积的微小透镜的制作实验和测量，多组实现的部分结果如图6所示，其中图6（a）为正置液滴不同体积光固胶液滴固化后透镜的轮廓，液滴体积分别是 V=1.65μL；2.35 μL；4.26 μL；6.80μL；图6（b）为不同体积下倒置液滴的非球面透镜轮廓图，液滴体积分别为V=1.50 μL；2.47 μL；4.66 μL；7.70 μL。 实验中虽然使用具有较高精度的移液器，但是由于光刻胶粘度和操作等，故上述所列的液滴体积为滴定后利用CCD成像拟合积分计算所得到的实际滴定的液滴体积。进一步可利用MATLAB对图6中微小透镜图像进行轮廓提取等处理，可得到透镜的面形轮廓数据。再利用描述透镜的圆锥曲线公式（2）对液滴轮廓进行拟合，即可以获取液滴透镜的底径和矢高，以及面形轮廓的非球面系数。

图6 正置和倒置液滴制作的透镜轮廓图Fig.6 The droplet profiles on silicate glass substrates

图6 所示的正置液滴和倒置液滴固化所得的透镜非球面系数K与体积V之间的关系分别如图7（a）（b）所示，图中散点为实验值，实线为相同实验条件下，包含实验体积在内的一定体积区间下的COMSOL理论计算拟合所得的结果。由图7可知，计算和实验结果具有很好的一致性；图7（a）所示的正置液滴，体积较小时其面型接近球面，当体积增大液滴快速偏离球面，体积V=6.80μL时，非球面系数K=0.9；对于倒置液滴，随着体积的增大，K值向负方向变化，变化相对稍缓慢（如V=7.70μL时，K=-0.7），但总体上仍是向数值较大的负方向变化。其主要是因为正置液滴表面张力的合力与体积力方向相同，使得液滴变扁平化的速度更快，而倒置液滴的体积力与表面张力的合力方向相反，表面张力削弱了体积力对液滴向下“拉长”的作用。

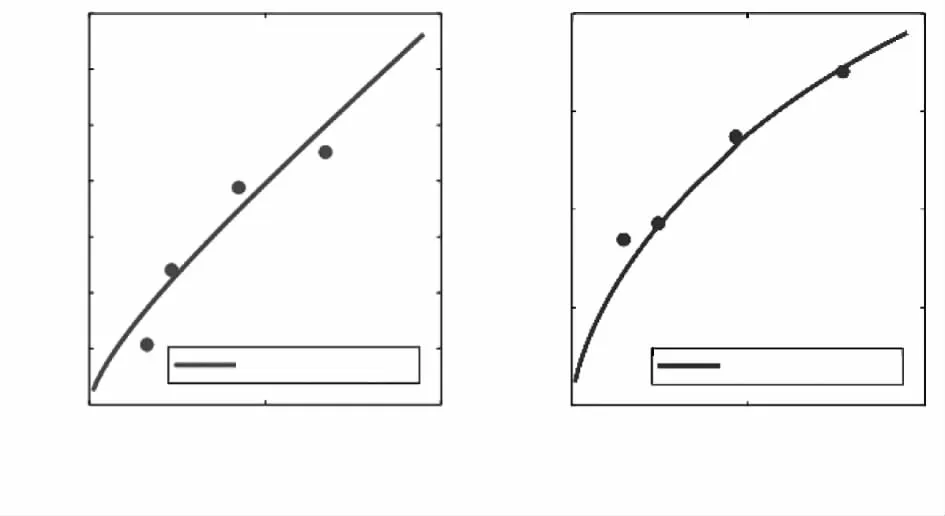
图7 液滴透镜的非球面系数与实验数据的对比图Fig.7 The comparison diagram between the theoretical and experimental data of the conic coefficient of the droplet lenses

3.3 透镜参数及光学性能

基于图6所示不同体积实验所得平凸型非球面微小透镜，其底径和对应的焦距分别如图8（a）、（b）所示，图中散点为实验测量值，实线和虚线为计算拟合后所得的结果；虚线为正置液滴对应透镜的参数，实线为倒置液滴所得透镜的参数。总体上，测量值与理论值具有较好的一致性变化趋势，随着体积的增大，透镜的底径增大，但是倒置液滴所得透镜底径的增大相对较为缓慢，且体积较大时较为显著，其是在体积不变的情况下，较大体积力的作用，液滴被向下“拉伸”，矢高增加，减小了底径随体积增加的变化量。对于图8（b）的焦距与体积的关系，由于正置液滴在较大体积力作用下，被“压扁”时的顶点曲率半径的增大显著。而倒置液滴所得透镜的焦距，由于液滴被较大体积力向下“拉伸”使得顶点曲率半径（f=R/（n-1））显著减小；但是，由于液滴在表面张力作用下，其面形为球面时，由球缺体积公式： （V=R3（2-3cosθ+cos3θ）） 知，其顶点曲率半径与体积关系为R∝V1/3，如图中点划线所示的球面轮廓焦距-体积曲线，随体积的增大，焦距f增大的速度逐渐减小。对于由表面张力和体积力共同作用的倒置液滴，虽然体积力向下“拉伸”使顶点曲率半径减小，但体积与焦距的关系总体上仍表现出平缓增长的趋势。

图8 液滴透镜的参数与体积的关系Fig.8 The relationship between the parameters and the volumes of the droplet lenses

图9 （a）、（b）为体积较小实验所得透镜的实物图和聚焦光斑测量图，图中正置和倒置液滴的i、ii所示透镜分别对应图6所示的I、II透镜轮廓；图9（b）为对应的聚焦光斑，正置液滴透镜i、ii的聚焦光斑RMS值分别为11.2μm、9.51μm；倒置液滴透镜i、ii的聚焦光斑RMS值分别为7.2μm、5.2μm；在相近体积下，倒置液滴透镜的聚焦光斑RMS值分别下降了36%和45%。表明倒置液滴所得的非球面系数K＜0的凸椭圆面形透镜具有更小的球差。

图10（a）、（b）为体积较大时，实验所得液滴透镜的实物图和成像测量图，图中iii、iv分别对应实验轮廓测量图6中III、IV号液滴透镜轮廓。由图（b）的成像图可见，倒置液滴所得非球面透镜的成像具有更为清晰的边缘，其成像效果明显优于相近体积下正置液滴的成像效果（如图10（b-I））。从而显示出倒置液滴所得K＜0的非球面透镜具有更好的综合光学性能。

图9 液滴透镜及聚焦光斑Fig.9 Droplet lenses and the focal spots

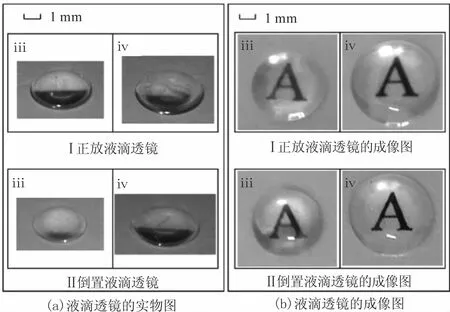
图10 液滴透镜及成像图Fig.10 Droplet lenses and the imaging

4 结 论

本文针对利用液滴法制作非球面微小透镜，基于流体动力学的液气两相流理论，并利用COMSOL建立层流液滴流动模型，计算描述了固体水平基底上的固着液滴和垂悬液滴在表面力和体积力共同作用下的液滴流动速度和压力分布，给出了不同体积力作用下正置和倒置液滴的面形演化趋势；结果表明，与正置液滴相比，倒置液滴法可以用来制作有利于提高透镜光学性能的、非球面系数K值均为负值的非球面微小透镜；并从仿真与实验两方面考察了接触角一定时，不同体积力对液滴面形轮廓几何参数的影响，结果具有很好的一致性。结果表明，正置液滴得到的是K＞0的扁椭球面形透镜，倒置液滴的非球面系数K＜0，且体积越大其数值越小，并具有更小的底径和焦距；进一步的透镜成像实验结果表明，相近体积下利用倒置液滴法制作的微小透镜比正置液滴透镜具有更好的聚焦性能与成像能力，在体积为1.6μL和2.4μL左右时，其聚焦光斑的RMS值分别减小了36%和45%，体积较大时成像也具有更为清晰的边缘和成像质量。相关工作表明调节体积力可以得到有利于获得具有较好光学性能的非球面透镜，也为进一步优化工艺，利用更大体积力的作用来制作非球面系数K＜-1的双曲面，甚至是K=-n2的理想双曲面面形的非球面透镜的制作提供了一定的基础。