基于共有星的快速星图识别方法
杨 上,周召发,刘先一
(火箭军工程大学兵器发射理论与技术国家重点学科实验室,陕西西安710025)
1 引 言
数字天顶仪是一种高精度天文定位仪器,在大地天文测量领域得到广泛应用[1-4]。星图识别为数字天顶仪定位提供起算数据,传统数字天顶仪的星图识别是采用三角形星图识别与坐标转换结合方法对旋转拍摄的16幅星图进行识别[5]。经大量实验发现,数字天顶仪在一次定位循环拍摄的16幅星图中存在着大量的共有星,即同一恒星会成像在多幅星图中的情况,若对拍摄的16幅星图上所有星点都单独进行识别,增加了星图识别的冗余量,降低了星图识别的效率,进而增加了数字天顶仪的定位所需的时间。对此本文提出了一种基于共有星的快速星图识别方法。该方法的核心思想首先对一个定位循环中在位置9和位置10拍摄的星图单独进行三角形星图识别,其次建立星点归算模型,找出剩余位置的星图与已识别星图间的共有星,最后对剩余星图上新增星单独进行识别,以此提高星图识别的速度。
本文首先介绍了单幅星图的三角形识别原理,其次通过构造辅助坐标系建立了倾斜修正模型,消除精调平状态下的小倾角,再在此基础上建立了星点归算模型,找出星图间的共有星,最后通过实验数据验证该星图识别方法的合理性。
2 数字天顶仪星图识别原理
数字天顶仪进行星图识别的导航星表是依巴谷星表,依据导航星表可得到恒星的赤经赤纬信息,再经视位置计算和时间补偿可得到恒星的天文经度α、天文纬度δ,则恒星的天球切平面坐标(ξ,η)可按下式计算:

其中,(α0,δ0)为GPS提供的概略天文经纬度。
恒星的理论CCD像点坐标为:

恒星的理论像距可按下式计算:

理想情况下,CCD平面为水平面,恒星星光通过数字天顶仪的焦距成像在CCD平面上,假设像点坐标为 (xm,ym) ,(xn,yn) ,则恒星像点像距按下式计算:

若恒星理论像点组成的三角形与恒星像点组成的三角形满足下式则匹配成功:

其中,ε为测量不确定度。
若对数字天顶仪拍摄的星图都采用三角形星图识别,则计算量较大,原因在于观测三角形与导航三角形容量较大[6],降低了数字天顶仪星图识别效率,对此数字天顶仪采用三角形识别与坐标转换相结合的方式进行星图识别,识别过程如下:
(1)采用三角形星图识别原理识别出6颗亮星。
(2)利用已识别出亮星的理论像点坐标与CCD像点坐标,建立仿射变换模型[7],如下式:
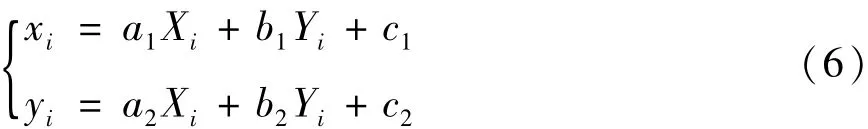
其中,仿射变换模型的参数可由最小二乘法计算得到。
(3)计算数字天顶仪视场内恒星的理论像点坐标。
(4)利用式(6)计算出转换后的恒星像点坐标(x′i,yi′) 。
(5)将转换后的像点坐标与CCD像点坐标进行匹配,若满足下式则匹配成功:

3 倾斜修正
传统的数字天顶仪星图识别是在精密整平状态下进行的,认为CCD平面是水平面,但即使在精调平状态下其CCD平面与水平面仍存在±10″内的小倾角[8],由下文第4节可知,建立的星点归算模型与CCD北向基准坐标有关,而北向基准坐标系的建立与水平面为基准[2],为此需要修正实际拍摄状态下存在的小倾角。
实际拍摄状态下,由文献[9]和文献[10]可知,经过较标的倾角仪敏感轴组成的平面与CCD平面平行,故可通过倾角仪测出CCD图像坐标系两坐标轴与水平面之间的夹角,假设CCD图像坐标系两坐标轴与水平状面之间的夹角θ1,θ2,可按下式计算得到:

式中,m,n为倾角仪的输出值;φ为倾角仪m轴与CCD图像坐标系x轴之间的夹角。
如图1所示,实线框为拍摄位置的水平面,坐标系O-xTyTzT为实际拍摄状态下CCD图像坐标系,其中CCD图像坐标系的坐标原点在CCD敏感器的中心,两坐标轴分别与CCD敏感器的两条边平行。OC,OD为OxT轴与OyT轴在水平面上的投影,OC,OD不一定垂直,则∠COxT=θ1,∠DOyT=θ2,AB为实际拍摄状态下的CCD平面与水平面之间的交线。

图1 CCD倾斜修正Fig.1 CCD tilt correct
由二面角的相关定理,可得实际拍摄状态下的CCD平面与水平面之间构成的二面角θ为:

如图1所示,构造辅助坐标系O-xFyFzF,其中OxF轴在实际拍摄状态下的CCD平面内且OxF⊥AB,OyF轴沿AB方向,OzF轴与OxF轴和OyF轴符合右手定则,OxS轴为 OxF轴的投影,则∠xFOxS=θ。设∠xFOxT=α,由二面角的相关定理可得:

根据方向余弦坐标变换原理可得存在方向余弦矩阵C1,可将坐标系O-xTyTzT中的星点坐标转换到坐标系O-xFyFzF中,即:
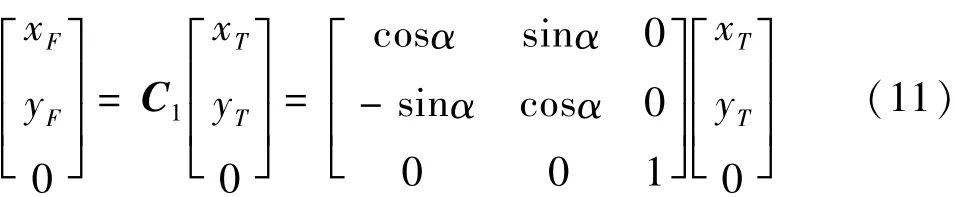
以水平面为基准,建立水平状态下的坐标系O-xSySzS,其中OxS轴为OxF轴的投影,OyS轴与OyF轴重合,OzS轴与OxS轴和OyS轴满足右手定则,则辅助坐标系O-xFyFzF可绕OyF旋转θ角与坐标系O-xSySzS重合,则在辅助坐标系O-xFyFzF中,存在方向矢量 (xF,yF, -f) 满足下式:

恒星位于无穷远处,发出的光为平行光,假设恒星成像在水平坐标系中的星点坐标为(xS,yS,0),则存在方向矢量(xS,yS,-f)满足下式:

化简上式可得:
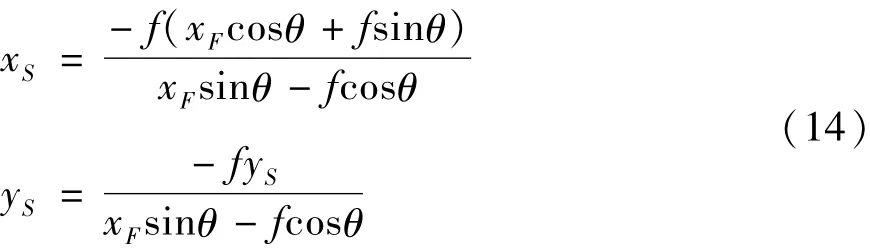
综上所述,通过构造辅助坐标系,依据倾角仪输出值和坐标变换原理,可得到恒星成像在水平面上的恒星像点坐标,并将式(14)称之为CCD像点修正模型。
4 星点归算模型
如图2所示,数字天顶仪旋转拍摄星图过程中,数字天顶仪在不同拍摄位置的视场存在重合,同一颗恒星可能成像在不同拍摄位置的CCD敏感器上。并且在拍摄过程中,CCD平面既有地球自转引起的转动,也有数字天顶仪自身的旋转引起的转动,为建立星点归算模型,需要考虑这两种转动引起的像点CCD坐标的变化。
首先考虑地球自转引起CCD平面的转动,以水平面为基准建立CCD北向基准坐标系O-xNyNzN,其中OzN轴过CCD敏感器中心并与垂直轴重合,OxN轴与纬线圈相切,方向指向东,OyN轴与经线圈相切,方向指向北。对于两个拍摄位置,假设数字天顶仪从前一拍摄位置旋转到下一拍摄位置,CCD北向基准坐标系由 O-xNyNzN变为 O-x′Ny′Nz′N,如图2所示。
初值时刻,水平状态下CCD图像坐标系O-xsyszs与CCD北向基准坐标系O-xNyNzN之间存在方位角A,根据坐标转换原理可得:

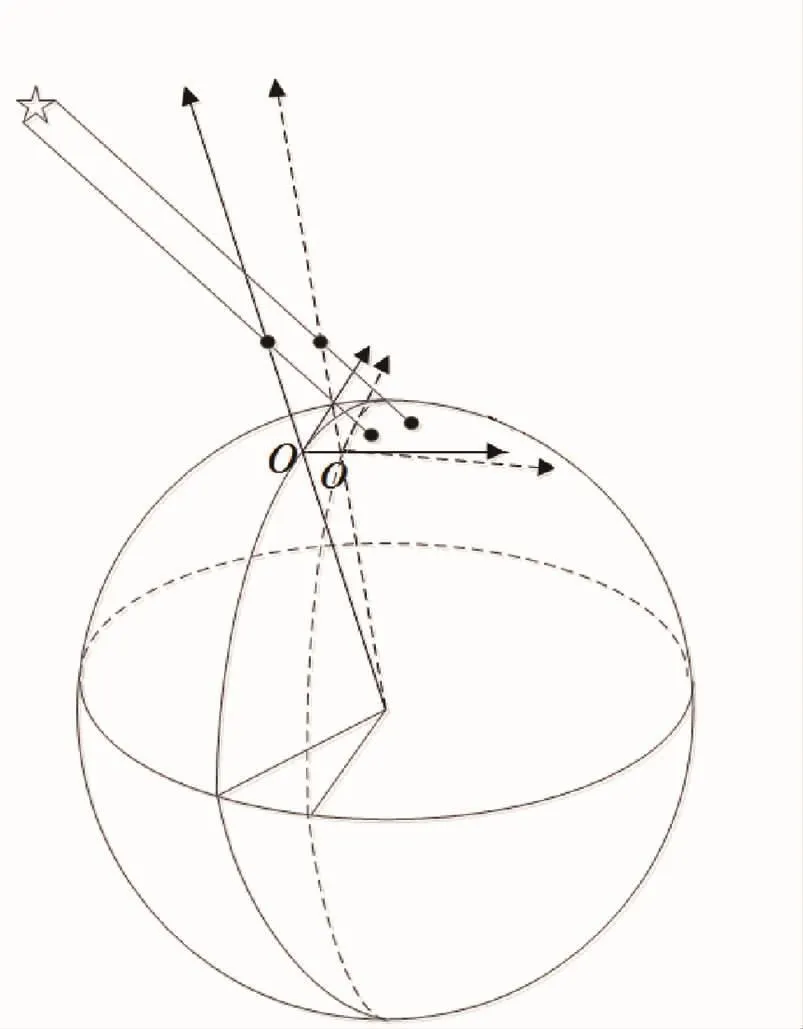
图2 CCD北向基准坐标系Fig.2 CCD north reference coordinate
其反变换为:

由第2节可知,在对单幅星图进行识别过程中建立了放射变换模型,其方位角A可由下式得到[8]:

在坐标系 O-x′Ny′Nz′N中存在与地球自转轴平行的方向矢量 u=(0,cosδ,sinδ) ,可使坐标系 O-xNyNzN绕旋转地轴旋转地球自转角θ后与坐标系O-x′Ny′Nz′N平行,则存在四元数 Q:
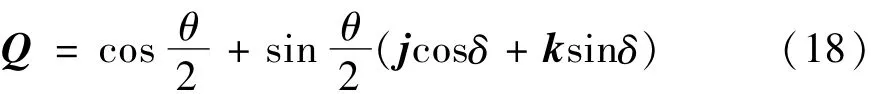
式中,θ=wret,wre为地球自转角速度。取wre=7.292115×10-5rad/s;t为拍摄任意两幅星图间的时间间隔,可由天顶仪测得输出;δ为测站点的天文纬度。


对于同一颗恒星,假设恒星成像在下一位置的CCD北向基准坐标系中的坐标为 (x′N,y′N,0) ,由于位于无穷远的恒星发出的星光可认为是平行光,则在下一位置的CCD北向坐标系O-x′Ny′Nz′N中,像点与焦点构成的方向矢量 r=(x′N,y′N, -f)满足:

由上式可得恒星成像在下一位置CCD北向基准坐标系上的坐标为:

坐标变换矩阵中包含未知数δ,由于位置9与位置10拍摄的星图已经单独识别出来,则可得到两幅星图上的共有星,故δ角可通过将位置9与位置10之间共有星的CCD图像坐标代入公式(21)求得。
联立公式(16)和公式(22),可得:

其次考虑数字天顶仪镜筒的旋转,假设数字天顶仪旋转角为φ,则:

式(24)称之为星点归算模型。
综上所述,为寻找位置1至位置8拍摄的星图与位置9拍摄星图之间的共有星,以及位置11至位置16拍摄的星图与位置10拍摄的星图之间的共有星,可按如下步骤进行:
(1)将数字天顶仪拍摄的16幅星图按式(11)计算得到辅助坐标系下的CCD图像坐标(xF,yF)。
(2)按式算出各位置在水平状态下的CCD图像坐标 (xS,yS) 。
(3)结合位置9与位置10得到的星图上的像点CCD坐标按式(24)进行计算,得到转换后的CCD图像坐标 (x′S,y′S) 。
(4)若满足下式,则表示位置9与位置10的星图与其他位置星图间存在共有星。

式中,ε为给定的阈值(一般取3pixel左右)。
5 实验结果分析
2017年11月,利用数字天顶仪采用在西安某地拍摄了大量星图,实验过程中数字天顶仪的焦距为(600±4)mm,数字天顶采用美国FLI公司生产的ML16803数码相机,CCD敏感器为Kodak公司生产的KAF-16803型面阵CCD。为实现对星图的识别,首先将依巴谷星表中恒星的位置信息转换拍摄时刻的视位置,在此基础上对星图进行识别,由于篇幅的限制,这里对一个定位循环的星图数据进行分析。其中表1为位置9星图识别的结果,表2为位置1星图识别的结果。
由表1与表2的星图识别结果可知,两幅星图之间的共有星为11颗,超过星图识别数量的50%,由此可见星图间存在着大量的共有星。
结合公式(24),将位置10星图上的星点坐标归算到位置16上拍摄的星图上,为直观表示出两幅星图上的共有星,可得到如图3所示。

表1 位置9星图识别结果Tab.1 Identification results of star map 9
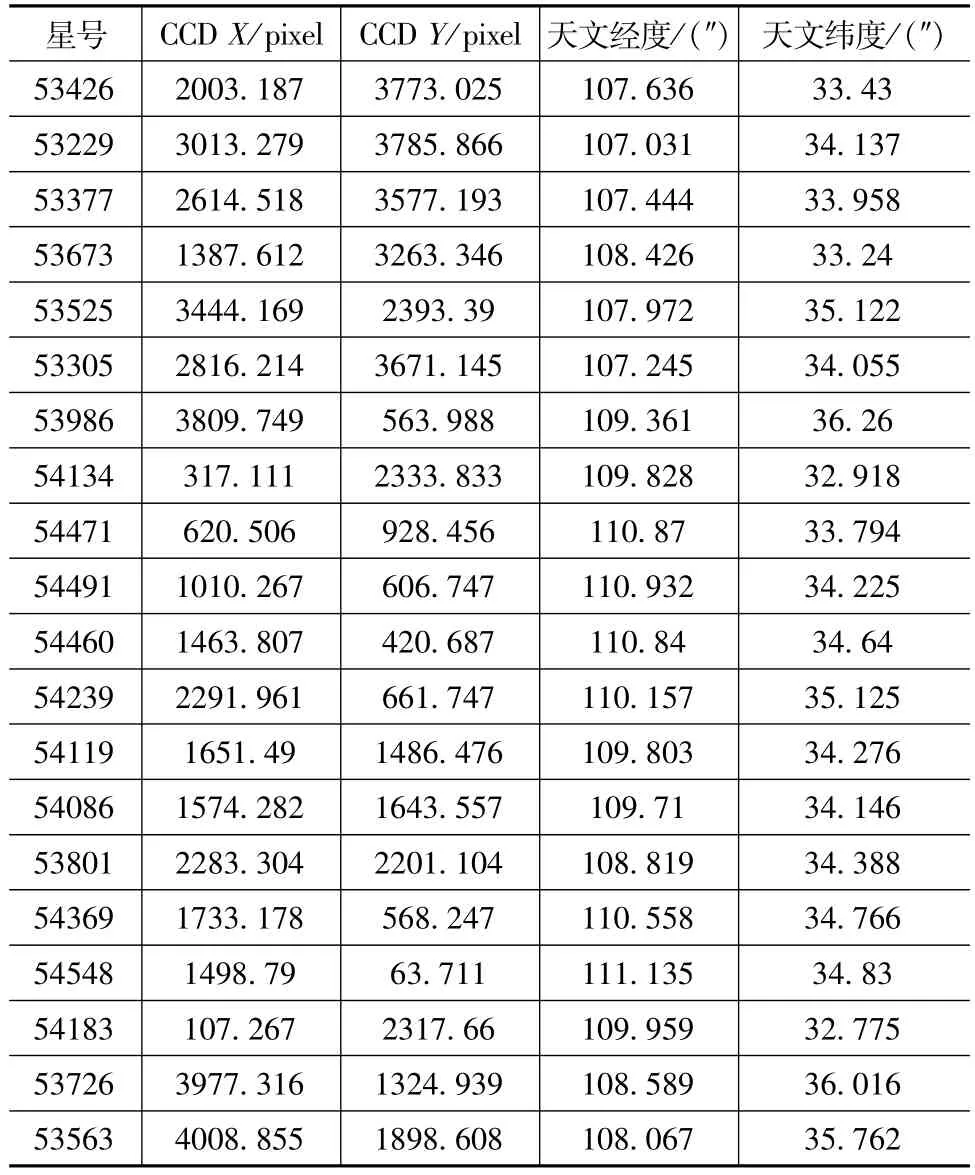
表2 位置1星图识别结果Tab.2 Identification results of star map 1

图3 共有星Fig.3 Common stars
由图3分析可知,位置10与位置16拍摄的星图上存在14颗共有星,且共有星的分布较为集中。其中将位置10星图上的共有星按式转换后,与位置16上共有星的CCD图像坐标相比,其中X坐标最大相差2.782 pixel,Y坐标最大相差2.629 pixel,X坐标与Y坐标最大差值均不超过3 pixel,由此可知由式(24)构造的坐标归算模型满足寻找星图间共有星的需求。
为进一步说明星图间存在着共有星,再任意选取一个定位循环拍摄的星图进行分析,将位置9星图上星点坐标归算到顺时针拍摄的8幅星图上来寻找与星图1至星图8与星图9的共有星,将位置10星图上的星点归算到逆时针拍摄的6幅星图上来寻找与星图11至星图16之间的共有星,如表4所示。

表4 共有星的数量Tab.4 The number of common star
由表4可知,与星图8之间的共有星最少15颗,与星图10之间的共有星最少为14颗。在实验过程中,利用数字天顶仪拍摄的单幅星图识别的恒星数量为25颗左右,通过坐标归算模型寻找出星图间的共有星,再对剩余的新增星单独进行识别,将大大提高星图识别的准确性。例如,假设一幅星图上有n颗观测星点,则可以组成C3n个观测三角形,有n颗导航星与其匹配,则可以组成C3n个导航三角形,并且假设每一个观测三角形需要与每次匹配后剩余的所有导航三角形匹配一次,那么对星图上所有的星点组成的观测三角形进行匹配,需要进行次匹配。若采用星点归算模型找出共有星后,假设存在j颗共有星,则对剩余的(n-j)颗新增星进行识别,则需要进行次匹配。在本次实验定位循环中,位置16提取出21颗观测星,与位置10之间存在14颗共有星,若对所有星点单独进行识别需要构建1330个观测三角形,并且需进行883785次匹配;若提取出14颗共有星后,只需要构建35个观测三角形,只进行45920次匹配,相比于原来,匹配次数大大减少,由此可以看出星图识别的速度得到较大的提高。
6 结 论
通过建立星点归算模型,能够依据位置9与位置10拍摄星图上星点信息找出其他星图上的共有星,单独对其他星图的新增星进行识别,将大大减少匹配三角形的个数和匹配的次数,提高星图识别的速度。
——环地平弧&环天顶弧

