基于VMD的激光雷达回波信号去噪方法研究

徐 帆，常建华，2，刘秉刚，李红旭，朱玲嬿，豆晓雷

（1.南京信息工程大学江苏省大气环境与装备技术协同创新中心，江苏南京210044；2.南京信息工程大学江苏省气象探测与信息处理重点实验室，江苏南京210044）

激光雷达是传统雷达技术和现代激光技术相结合的产物，具有分辨率高、探测性能好、抗干扰能力强等特点［1］，被广泛应用于大气遥感，如探测大气气溶胶、边界层、云、风、能见度等［2-4］。在实际应用中，激光雷达回波信号的强度随探测距离的增加而减小，而且其中夹杂着各类噪声，特别是白天强烈的太阳背景光将会导致信号完全淹没在噪声之中［5］，这将直接影响激光雷达的有效探测距离和精度。因此，采用有效的噪声滤除方法，提取背景噪声中的有用信号是实现激光雷达全天候、高精度探测的关键［6］。

激光雷达回波信号是典型的非线性非平稳信号，为滤除这类信号中的噪声，卡尔曼滤波（KF）、小波变换（WT）、经验模态分解（EMD）等技术被先后引入。KF是一种以最小均方误差为估计最佳准则来寻求递推估计的算法，能够对时变系统、非平稳信号、多维信号进行处理，但信号发生急剧变化时，该方法会造成极大的误差［7］。WT可以通过多尺度分析将信号分解为不同的频率分量，具有良好的时频局部化特性，但存在小波基函数的选择问题，自适应性较差［8］。EMD弥补了WT的不足，具有良好的自适应性，可以极好地反映信号的局部频率特征，但其在理论上缺乏严格的数学证明，且存在端点效应、模态混叠等问题，对信号的后续分解产生干扰，使得分解结果不能有效地将有用信号与噪声分离，影响去噪效果［9-10］。 2014 年，Konstantin Dragomire等提出了变分模态分解（Variational Mode Decomposition，VMD），它是一种新的自适应信号处理方法，对非线性、非平稳信号的处理具有明显的优势［11］。该方法运算效率高，可克服EMD中的模态混叠问题，实现信号的准确分离，利用其自身具有的维纳滤波特性可获得更优的噪声滤除效果。目前VMD去噪方法，大多采用局部重构法［12］，但处理激光雷达回波信号时，单纯的采用局部重构法（VMD-PR），在恢复信号的同时会导致信号的部分丢失。

本文提出了一种VMD与巴氏距离、移动平均相结合的激光雷达回波信号去噪方法（简称为VMD-BDS）。该方法利用去趋势波动分析（DFA）对回波信号进行VMD分解，通过巴氏距离计算信号和对应的各个模态分量概率密度函数（PDF）之间的相似性，从而获得相关模态与非相关模态。在此基础上，采用移动平均法对非相关模态进行处理，提取其中的有用信号。最后，将相关模态和处理后的非相关模态进行重构实现去噪。

2 VMD原理

VMD算法通过迭代搜寻变分模型最优解来确定每个固有模态分量（BLIMFs）的中心频率和带宽，实现信号从低频到高频的有效分离，其过程实质上是变分问题的求解过程［11］：首先，构造假设每个模态是具有中心频率的有限带宽，描述为寻求K个模态，使得每个模态的估计带宽之和最小，约束条件为各模态之和等于输入信号f的变分问题。其模型为：

其次，对构造的变分问题求解。二次惩罚因子可以保证信号在噪声环境下的重构精度，拉格朗日惩罚算子可使约束条件更为严格。因此，通过引入二次惩罚因子α和拉格朗日惩罚算子λ（t），将式（1）所述的约束性变分问题转换为非约束变性分问题，获得增广拉格朗日表达式如下：

根据Parseval/Plancherel傅里叶等距变换，可将式（3）转换到频域，并对此最小值问题求解得：

VMD算法的具体过程如下所示：

（2）根据式（4）和式（5）在频域内更新 uk、ωk；

（3）根据 λˆn+1(ω)=λˆn(ω)+τ（ˆf（ω）-∑（ω）） ，不断更新 λ；

3 基于VMD的去噪算法原理

3.1 VMD分层

在利用VMD对信号分解时需要设置分解层数K，不同K值的选取对分解结果有较大的影响。DFA是一种计算时间序列长程相关性标度指数的方法，它可以将各种不同阶的外来趋势从时间序列中清除，从而准确地观察到时间序列本身所具有的统计行为特征［13］，更适于分析非平稳信号。经研究发现，VMD分解层数K与输入信号的标度指数有关，因此，通过数据分析，建立了K与输入信号的标度指数 α0的关系模型［14］：

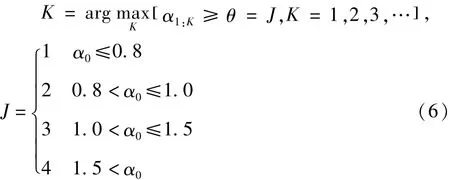
式中，K是VMD分解层数；α1：K是每个模态分量的标度指数；阈值θ=α+0.25，对于高斯白噪声，一般α取0.5［15］；J是模态分量的标度指数大于阈值的个数；α0是输入信号的标度指数。

3.2 相关模态的选择

PDF可以反映信号分布之间的差异，为此，我们用核密度估计的方法获得输入信号和每个模态的PDF［16］，通过计算它们之间的相似性，来区分相关模态和不相关模态。而巴氏距离可用于测量两个PDF之间的距离，是证明相似性的一种有效方法。在同一定义域X中，概率分布P和Q的巴氏距离定

义如下：

其中，对于离散概率分布：

对于连续概率分布：

DB越小，表示概率分布越接近，模态分量与输入信号越相关。

模态分量与输入信号之间的相似性L()i定义如下：

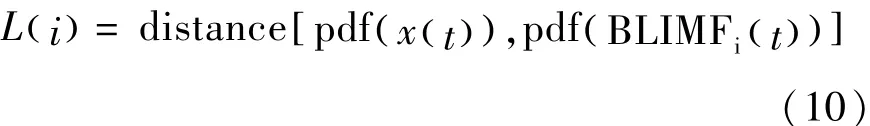
相关模态可以通过评估相邻两个模态与输入信号距离之间的斜率来确定［17］。我们定义θ为相邻两个模态与输入信号距离之间的最大斜率，

相关模态和非相关模态的分界点为Kth=i。

3.3 非相关模态处理

目前VMD去噪方法，大多采用局部重构法，其直接将非相关模态去除（认为是噪声）。但在处理激光雷达回波信号时，非相关模态中也会有少量的有用信号存在。因此，利用移动平均法，对非相关模态进行处理，提取其中的有用信号。移动平均法原理是将输入信号按照设定的滤波点数进行数学平均作为其输出信号，数学表达式为：

式中，k=1，为3点移动平均；k=2，为5点移动平均，……。

4 仿真实验与分析

激光雷达系统中存在各类噪声，严重影响了回波信号的信噪比，这些噪声一般可当作高斯白噪声处理。根据激光雷达方程，对激光雷达回波信号进行仿真，叠加10 dB的高斯白噪声，如图1所示。

其中，P（r）是探测到的回波功率；c是光速；r是探测距离；E0是发射激光脉冲能量；Y（r）是激光雷达几何重叠因子；Ar是望远镜接收面积；β（r）是r处目标的后向散射系数；T（r）是大气透过率；TtTr是发射和接收光学系统的总透过率。

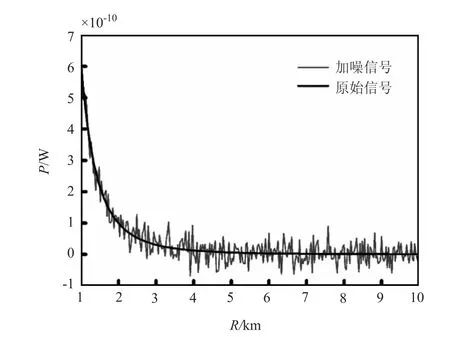
图1 激光雷达回波信号仿真Fig.1 Simulation of lidar echo signal

根据式（6）分解层数与输入信号的标度指数的关系模型，利用DFA对仿真的激光雷达回波信号进行VMD分解，得到11个固有模态分量，各分量从低频到高频分布，分解结果如图2所示。用核密度估计的方法获得输入信号和每个模态分量的PDF，根据式（7），获得它们之间的巴氏距离，如图3所示。观察此图可知，BLIMF1与BLIMF2之间的斜率最大，因此BLIMF1被认为是相关模态，其余分量被认为是非相关模态，利用移动平均法对非相关模态进行处理，提取其中的有用信号。通过重构相关模态和处理过的非相关模态，进而得到去噪后的回波信号。

图2 仿真回波信号的VMD分解结果Fig.2 VMD decomposition results of simulated echo signal

为了验证VMD-BDS算法在回波信号去噪处理中的有效性，采用输出信噪比SNRout和均方根误差RMSE作为其评价指标，SNRout可以反映算法的去噪性能，其值越高，说明去噪性能越好；RMSE可以反映去噪信号和原始信号之间的相似度，其值越小相似度越高［18］。两个评价指标定义分别如下：

图3 各模态与回波信号间巴氏距离Fig.3 Bhattacharyya distance between modes and echo signal

其中，f()k为原始信号；f′()k为去噪信号；k为信号长度。

目前，WT和EMD直接阈值（EMD-DT）去噪已应用于激光雷达回波信处理中，并取得了良好的效果，而对于VMD，大多采用VMD-PR来实现去噪。为了进一步说明本文方法的优越性，采用WT-db4（基函数为 db4）、EMD-DT、VMD-PR对仿真的激光雷达回波信号进行去噪处理，并与VMDBDS的去噪性能相比较。四种方法去噪后的比较如图4所示。由图4可以看出，四种方法都基本保留了回波信号的趋势，但经WT-db4、EMD-DT处理后的信号依旧存在少许“毛刺”，经VMD-PR处理后的信号，近距离处出现了失真现象，与这三种方法相比，VMD-BDS具有最佳的平滑效果，且经其处理后的信号也不存在失真问题。

四种方法的去噪性能由表1所示，观察表1可知，当输入信噪比为10 dB时，经VMD-BDS、WT-db4、EMD-DT、VMD-PR四种方法处理后的回波信号，SNRout分别提高为 22.58 dB、20.29 dB、22.39 dB和13.43 dB，而 RMSE分别为 0.78、0.99、0.98和2.20。VMD-BDS方法具有最高的SNRout和最小的RMSE，表明其保证了回波信号的完整性，并且使去噪后的信号与原始回波信号更加接近。因此，VMD-BDS在处理激光雷达回波信号方面有一定的有效性和优越性。

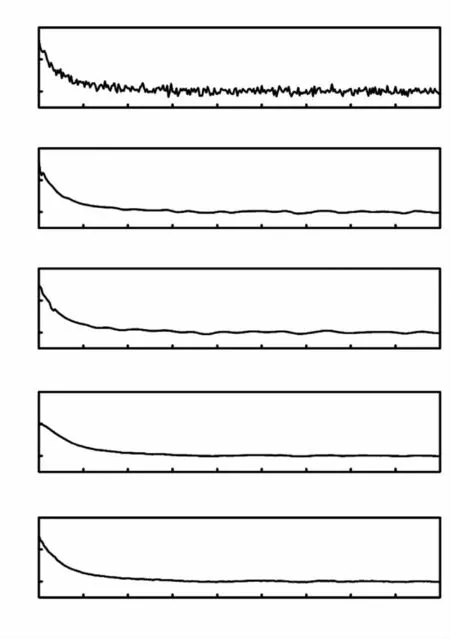
图4 四种方法的去噪比较Fig.4 Comparisons of de-noising for four methods

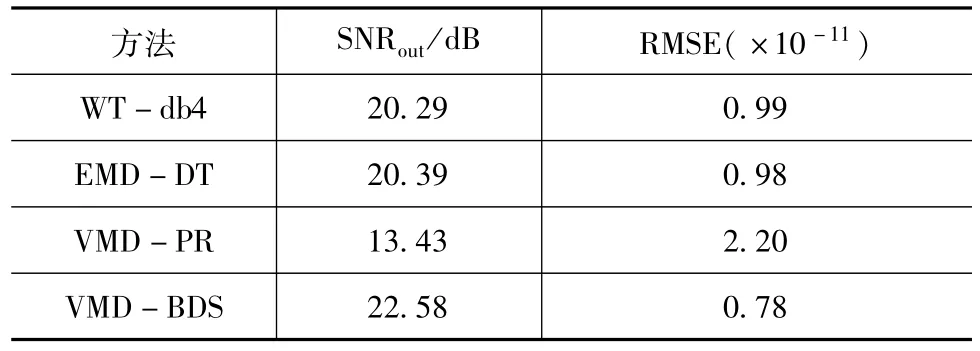
表1 四种方法的去噪性能Tab.1 Performance of four de-noising methods

5 VMD-BSD在实测激光雷达信号处理中的应用

为了更好地评价所提方法的去噪效果，我们将该方法用于实测激光雷达回波信号。此信号由置于南京信息工程大学内的瑞利-拉曼-米散射激光雷达（RRML）的米散射通道测得（地理坐标为118.7°E，32.2°N），该激光雷达由安徽光机所研制，发射单元采用调Q倍频Nd∶YAG激光器，波长为532 nm，重复频率为20 Hz，脉冲能量约为200 mJ；后向散射回波信号被直径为400 mm的望远镜接收，利用H5783型光电倍增管（PMT）检测信号，通过A/D采集数据卡采集信号。

激光雷达实测回波信号随高度的增加而衰减，由于受到噪声的影响，回波信号波形起伏明显，存在许多“毛刺”。利用VMD-BDS对此信号进行去噪处理，使得SNRout提高到了26.15 dB，去噪效果如图5所示。从图中可看出，经VMD-BDS处理后的信号保持了回波信号的变化趋势，整体十分平滑，噪声滤除效果明显。说明该方法对高频噪声有很好地抑制作用，能使真实信号与噪声信号有效分离，可为提高后续数据反演精度打下基础。

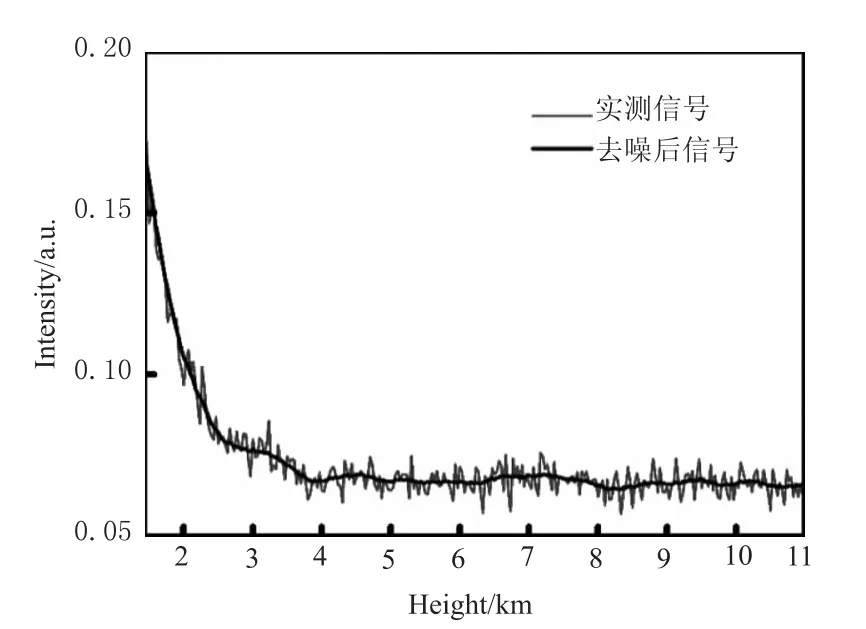
图5 实测激光雷达回波信号去噪效果Fig.5 Results of de-noising for measured lidar echo signal

6 结 论

为滤除激光雷达回波信号中的噪声，提取其中的有用信号，本文提出了一种基于VMD的回波信号去噪方法。该方法利用DFA对信号进行VMD分解，通过计算巴氏距离区分相关模态和非相关模态。在此基础上，采用移动平均法对非相关模态处理，最后将相关模态和处理后的非相关模态进行重构实现去噪。仿真结果表明，VMD-BDS处理后的信号SNRout为 22.58 dB，RMSE为 0.78 ×10-11，与 WT-db4、EMD-DT、VMD-PR相比，具有最高的 SNRout和最小的RMSE，其去噪效果明显。同时，利用此方法对实测激光雷达信号进行处理，具有较好的平滑效果，保持了原信号的特征，表明了此方法的可行性与优越性。