一种深度强化学习的雷达辐射源个体识别方法

冷鹏飞， 徐朝阳

(中国船舶重工集团有限公司 第723研究所, 江苏 扬州 225001)

0 引言

在雷达对抗领域中，雷达辐射源识别技术是电子对抗情报分析领域中的重要研究内容，其水平是衡量电子侦察系统和侦察设备信息处理技术先进程度的重要标志[1]。雷达辐射源个体识别技术通过脉内无意调制特征区分雷达的不同个体[2]，当前雷达辐射源识别问题的一个研究热点为提取辐射源的有效特征[3]，通常可将信号包络特征[4]、高阶矩[5]、时频特征[6]以及模糊函数特征[7]等参数作为辐射源的个体特征。这些特征均需基于先验知识人工提取，因而所提取特征未必能描述辐射源的本质特点，且人工提取特征过程繁琐，使得数据库更新缓慢。

近年来，深度神经网络的兴起使得机器自动提取特征成为现实，深度神经网络可逼近复杂的非线性函数，具有较强的泛化能力，能够刻画数据本质信息[8]，且现场可编程门阵列(FPGA)、图形处理单元(GPU)的加速处理方法使得运算的实时性得以保证。基于此，本文提出了一种深度强化学习的辐射源个体识别方法，利用不同雷达个体发射信号包络的差异实现辐射源识别，在实际电子对抗环境中，雷达辐射源脉冲宽度从微秒级到毫秒级变化，这种大范围的脉宽变化使得处理整个辐射源包络较为困难，考虑到工程应用中系统的实时性要求，本文将辐射源包络前沿(包络上升沿及其前后部分数据) 作为个体特征进行辐射源识别。

1 辐射源包络

1.1 辐射源侦收

图1给出了一种电子侦察设备个体识别框图，为了兼顾宽带接收机侦察范围大、窄带接收机灵敏度高的优点，本文采用一种宽带、窄带接收机并行工作的方案。宽带接收机对信道带宽进行子信道划分，进而完成各频段辐射源信号的检测与参数估计以获取宽带脉冲描述字(PDW)样本集；窄带接收机分时侦收各频段辐射源信号，对射频前端中频输出进行采样、信号检测及参数估计以获取窄带PDW样本集；宽带、窄带PDW样本集经数据融合后再对其融合结果进行信号分选。信号分选后的辐射源描述字(EDW)将作为个体识别模块的控制信号，依据窄带PDW样本集选择感兴趣的辐射源脉冲s(n)对其进行个体识别，其中n为离散时间。

1.2 辐射源包络提取

设窄带接收机侦收辐射源基带信号为s(n)，则其包络可描述为

(1)

式中：Hilbert[·]为希尔伯特变换。对a(n)进行滑动平均处理可获得平滑的包络曲线，以上升沿中点对齐信号包络，可截取一段包络前沿作为深度神经网络的输入。图2给出了两类雷达个体辐射源包络前沿，图2中每类辐射源有10个样本，接收机带宽为200 MHz，采样频率为1 GHz，信噪比SNR≥15 dB. 从图2中可以看出，两类辐射源包络上升沿形状、过冲点均存在差异，表明不同辐射源个体可通过包络前沿区分开来。

2 深度强化学习

2.1 马尔可夫决策过程

讨论强化学习模型在C类已知辐射源识别问题中的应用。强化学习任务通常用马尔可夫决策过程(MDP)来描述，MDP对应四元组，其中：S为输入状态集合，s∈S为某个特定状态；A为可选动作集合，a∈A为某个特定动作；p为当前状态s在机器执行动作a后转化为状态s′的概率；r为当前状态s在机器执行动作a后转化为状态s′时所获得的奖励。MDP具有马尔可夫性质：系统下一时刻状态只与当前时刻状态有关，与过往时刻状态无关。在所述辐射源识别任务中，状态s为电子侦察设备从外部电磁环境侦收提取的辐射源包络前沿；a为辐射源类别编号0，1，2，…，C-1；奖励r依据模型识别结果与雷达数据库中样本真实类别的异同而定，相同时r取+1，不同时r取-1；对于状态转移概率p而言，尽管下一时刻辐射源包络前沿s′与当前时刻状态动作对(s,a)无关，但是在网络训练过程中，为了防止过拟合，通常会随机乱序训练样本且各训练样本数目分布均匀，因此可以认为状态转移概率p=1/C，且s′仅在状态s下执行动作a时以概率p转移而得，与过往时刻的状态无关，即满足马尔可夫性质。

2.2 策略

在强化学习中，对于当前输入状态s，机器在某种策略π的指引下选择动作a=π(s)，机器学习的目的即为求得最优策略π*. 通常可用状态- 动作值函数(即Q值函数)评估策略，其数学模型为

(2)

式中：γ为折扣系数，其值在0～1之间，γ的存在是为了确保长期累积奖励能够收敛。

(2)式描述了从状态s出发，执行动作a后使用策略π所带来的期望累积奖励，对其进一步推导可得Bellman方程为

Q(s,a)=Es′[r+γEa′～π(s′)[Q(s′,a′)]|s,a,π]，

(3)

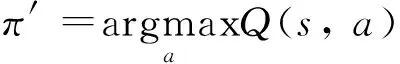
(4)

式中：Q*(s,a)为使用最优策略π*时所产生的期望累积奖励。(4)式明确了机器学习的方向，即使得Q值函数收敛于最优Q值函数Q*(s,a)的方向。

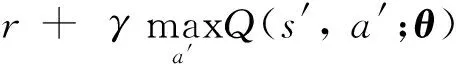
(5)

(5)式使得Q值函数依据ε-贪心策略在最小均方差意义下收敛于最优Q值函数Q*(s,a).

在深度学习任务中，输入向量的维数一般较高，即使最优化问题中损失函数在某点处的梯度为0，其在该点所有分量上呈现出相同凹凸性的概率亦几乎为0，因此，深度学习中损失函数梯度为0的点更多地考虑为鞍点而非局部最优点，由于梯度噪声的存在使得网络能够跳出鞍点，因而(5)式可用随机梯度下降类算法求解。

3 具体网络模型

3.1 深度Q网络模型

本文讨论10类已知雷达辐射源的个体识别问题，输入辐射源包络前沿长度为1 024，以卷积神经网络[10]拟合Q值函数，图3给出了其模型，该模型为深度Q网络(DQN)模型[11]，由2层卷积池化层、3层全连接层组成。第1层卷积层卷积核大小为5×1，提取辐射源包络前沿6个底层特征，第2层卷积层进一步提取包络前沿高层特征，池化层使用某一位置相邻输出的总体统计特征代替网络在该位置的输出[12]，通过对卷积层输出特征图中相邻像素点取最大值的方式实现池化运算，使网络在保留辐射源本质特征信息的同时可以减少数据量。全连接层用于将这些特征连接起来，多层全连接层级联能够增强网络的学习能力。

对于辐射源包络前沿s，经过网络正向传播后即可得到当前状态s下执行各动作时的Q值，即Q(s,a；θ)，其中a为整数0,1,…,9.

经过训练后，网络将收敛至最优Q值函数。由于目标Q值函数与Q值函数之间存在相关性，深度强化学习模型在训练时难以收敛，为了缓解这个问题，可在Q值函数拟合网络多次迭代后更新一次目标Q值函数以降低其相关性，即将(5)式变为

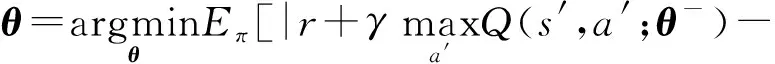
(6)

式中：参数向量θ-在多次迭代后得到参数向量θ.

3.2 深度双Q网络模型

DQN模型以卷积神经网络拟合Q值函数，进而通过梯度下降类算法求解(6)式最优化问题，分析(6)式可知，其目标Q值函数采用同样的拟合函数选择最优动作并对其进行评估，即有

(7)

在这个过程中，θ-并没有更新，这种方式会导致Q值的高估，若这种过高的估计对于所有潜在决策是不一致的，则可能导致策略选择次优解[13]。对于状态空间连续取值的强化学习任务来说，有限的学习样本不能使神经网络拟合出适用于所有状态动作对的Q值函数，因此所拟合的Q值函数曲线会在真实Q值曲线周围波动。由于目标Q值函数值求解过程中需要选择，使得Q值达到最大的动作，网络估计的Q值可能比真实Q值高。深度双Q网络(DDQN)模型采用两个卷积神经网络，分别用于选择最优动作和策略评估，缓解了这个问题，其目标Q值数学模型为

(8)

在实际应用时，与(6)式中降低目标Q值函数与Q值函数相关性的方法类似，可以用一个网络实现，即参数向量θ-为参数向量θ多次迭代前的向量。

3.3 Dueling Network模型

与DQN模型不同，Dueling Network模型[14]将Q值函数分解为状态值函数V(s)与动作优势函数A(s,a)，其数学模型为

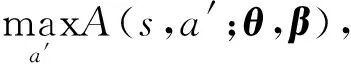
(9)

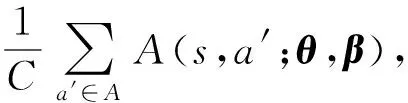
(10)

式中：α、β分别为状态值函数与动作优势函数全连接层的参数向量。Dueling Network模型与DQN模型的区别在于最后一层全连接层，DQN模型直接拟合Q(s,a)，而Dueling Network最后一层由并联的两个全连接层组成，拟合A(s,a)的全连接层与DQN模型相同，输出C个通道，而拟合V(s)的全连接层只有一个输出通道。为了便于论述，记(9)式为“极值法”、(10)式为“均值法”。网络收敛后，极值法中V(s)、A(s,a)能够给出状态值函数及动作优势函数的估计[14]，但是(9)式使得网络难以收敛；均值法中V(s)、A(s,a)在网络收敛后与实际估计存在一个常数偏差，但(10)式能够保证网络稳定收敛。图4给出了网络训练过程中两种Q值拟合方法的Q值曲线以及训练精度- 迭代次数曲线(具体仿真实验参数见第4.1节、4.2节)。为了清楚地对比两种方法的性能，图4中曲线为实际曲线均匀降采样的结果，图4中平均Q值为64个辐射源包络前沿Q值的平均(动作为使Q值最大的动作)。从图4中可以看出，均值法Q值、训练精度稳定上升，且训练精度逐渐收敛。Q值曲线仍呈现上升趋势的原因是(2)式中γ为0.99，理想情况下网络收敛时奖励r恒等于1，因而理论上最优Q值为100，在分类识别任务中，长时间的迭代会导致模型过拟合，因此当模型训练精度满足工程需求时即可停止训练。

4 实测数据仿真实验

4.1 实验环境

实验平台为Ubuntu Linux16.04，深度学习模型架构为TensorFlow，程序接口为Python 2.7，图形处理器为NVIDIA GeForce GTX 1080Ti. 为了确保深度学习模型可靠泛化，主要考虑3个方面问题：1)模型对不同型号、不同雷达个体辐射源信号的识别能力；2)模型对相同型号、不同雷达个体辐射源的识别能力；3)模型对不同接收系统所侦收辐射源的识别能力。为此，样本集中含同型号导引头辐射源信号4类、同型号机械扫描雷达辐射源信号4类、同型号雷达模拟器辐射源信号2类，共10类辐射源样本，每类样本数据量为6 000，其中训练集样本数量为54 000，测试集样本数量为6 000，训练集与测试集中各辐射源类别数量分布均匀。雷达辐射源经不同侦收系统采集，利用抽取、插值等处理方法将信号采样率统一为1 GHz，对齐包络后取1 024个离散样本点作为辐射源包络前沿数据。图5为某雷达个体辐射源包络前沿(10个样本)。从图5中可以看出，样本集中相同雷达个体辐射源包络前沿间亦存在差异。因此，可用模型的测试精度评估其泛化能力。

4.2 模型训练

模型训练步骤如下：

1)采用Xavier方法[15]初始化拟合Q值函数的网络参数向量θ；

2)初始化拟合目标Q值函数的网络参数向量θ-；

3)对于当前输入状态(辐射源包络前沿)s，利用ε-贪心算法选择动作a(某个类别)；

4)若a与雷达数据库中的样本真实类别相同，则获取奖励r=+1，否则r=-1；

5)载入下一时刻状态s′，利用(8)式计算目标Q值函数y(DQN模式为(7)式)；

6)对|y-Q(s,a;θ)|2使用梯度下降类算法更新网络参数θ；

7)每D次迭代使得θ-=θ；

8)重复步骤3～步骤7，直至网络收敛。

模型训练参数如下：学习率为0.000 25，minibatch大小为64，迭代次数为2 000，参数更新周期D为15，概率ε=0.5×0.02i/1 500(i为当前迭代次数)，折扣系数γ为0.99，采用Adam算法训练网络，其中梯度动量β1为0.9，梯度平方动量β2为0.999，引入误差e为10-8以确保计算过程数值稳定。

图6为3种模型的训练结果，为了清楚地对比3种模型的性能，图6中曲线为实际曲线均匀降采样所得。从图6中可以看出，3种模型训练精度均已收敛，且DDQN模型、Dueling Network模型的Q值估计低于DQN模型。图6(a)中存在许多训练精度瞬间下降的毛刺，这是因为迭代初期机器不断选择非最优动作导致的，图6(a)中ε-贪心策略的概率ε随着迭代次数的增加而降低，在迭代初期ε较大，机器会以较大概率选择非最优动作训练网络，因而毛刺较为密集；随着ε的减小，这种现象得以缓解。事实上，在测试时机器总是选择最优动作执行，因此这些毛刺不会对网络测试精度造成影响。

4.3 测试结果

测试实验对比了传统机器学习算法与深度神经网络的识别性能，其中，k近邻(k-NN)算法的近邻数k取20，以L1范数与L2范数两种方法度量待识别辐射源包络与已识别样本的距离，支持向量机(SVM)采用线性函数(linear function)与径向基函数(RBF)作为核函数，对辐射源包络进行识别。表1为各模型运算时间对比，其中训练平均时间为模型训练时1个minibatch(使用梯度下降类算法求解最优化问题过程中单步迭代参与运算的样本数据，即64个辐射源包络前沿)平均每次迭代所消耗的时间，测试平均时间为测试模型识别能力时1个minibatch数据正向传播过程所消耗的时间，其值为多次实验的平均结果。分析表1中数据可知，3种模型可实时实现且运算时间大致相当，这是因为3种模型中运算复杂度较高的深层网络结构相同，其差别仅在于Q值函数、目标Q值函数的拟合方式。在实际工程应用时，可将一台服务器专门用于模型的训练，并将训练完成的网络参数即时传输给FPGA(或PowerPC等实时处理设备)，最终的辐射源识别功能则交由FPGA(或PowerPC)完成。表2为测试精度对比，从表2中可以看出，传统k-NN算法、SVM算法识别率不足80%，而本文所述3种深度神经网络模型识别率均在96%以上，且Dueling Network模式识别率高达98.42%.

表1 3种模型的运算时间对比

表2 7种模型的测试精度对比

5 结论

本文讨论了深度强化学习在已知雷达辐射源个体识别中的应用。从用于辐射源个体识别的电子侦察设备方案出发，分析了深度强化学习理论在辐射源识别中的具体表现形式，给出了DQN模型、DDQN模型以及Dueling Network模型3种具体网络模型，实测数据仿真实验结果表明，相较于传统机器学习算法而言，深度强化学习算法能够在保证一定运算实时性的同时取得更高的识别率。