某大口径机枪内膛损伤对弹头挤进过程的影响研究

沈超， 周克栋， 陆野， 乔自平

(1.南京理工大学 机械工程学院， 江苏 南京 210094；2.中国兵器工业第208研究所， 北京 102202)

0 引言

机枪连发射击过程中，枪管受到较高频率的火药燃气瞬态热作用、化学作用、机械摩擦作用(包括弹头和火药燃气中的固相颗粒)以及膛压作用，枪管内膛会出现诸如裂纹、烧蚀坑等损伤。大量试验显示，即使在枪管内壁镀上一层甚至多层耐高温、耐腐蚀和耐磨损的铬层以保护枪管基体材料，铬层仍会在射击寿命试验的前期就出现裂纹，并随着射击过程的进行，裂纹不断加深加宽，并出现剥落，基体在失去铬层保护之后便会快速烧蚀磨损，导致枪管寿终。寿命试验表明，大口径机枪的寿终常表现为椭圆弹孔率的超标，而坡膛的结构损伤是造成枪管产生椭圆弹孔的根本原因[1]，弹头挤进过程是一个具有高瞬态、高温强冲击、高速摩擦、大变形等特点的瞬态动力学过程[2]，内膛损伤导致的内膛结构及尺寸的细微变化都会对弹头挤进过程的受力及运动姿态产生较大影响，进而影响整个内弹道过程。

近年来，国内外多位学者对弹- 枪耦合过程及弹枪耦合退化内弹道进行了研究，并取得了一些成果。文献[3-5]对枪管有无磨损下的内弹道过程进行了理论研究，但均未涉及挤进过程的大变形塑性力学及弹头材料的损伤失效。文献[6]对火炮身管失效机理进行了研究并提出了基于火炮身管外壁面应变变化量预测身管寿命的方法。文献[7]建立了考虑弹头塑性大变形及断裂失效的弹带挤进身管坡膛的有限元模型，研究了挤进过程中弹带塑性变形流动及弹带的断裂失效模式。文献[8]对某狙击步枪的弹- 枪耦合作用过程进行了研究，建立了弹- 枪相互作用数值计算模型，针对弹- 枪结构参数变化对弹头膛内运动过程的影响进行了分析。文献[9]基于试验获得了火炮不同寿命阶段内膛的烧蚀磨损情况，并建立理论模型研究了由于内膛烧蚀磨损而引起的火炮弹道寿命变化情况。文献[10-11]建立了磨损内膛的弹- 炮耦合模型，采用参数化方法对身管内膛进行建模，分析了火炮内弹道膛压和弹丸初速随内膛损伤的退化过程。

以上对弹- 炮、弹- 枪耦合作用的研究中，身管内膛损伤的表现形式主要局限在内膛的磨损量上，不论是以磨损最大处磨损量(文献[9]中称该处为磨损特征点)代替整个内膛的磨损量，抑或是对身管分段建模，考虑身管不同截面处磨损量的差异，均只考虑了内膛磨损对弹- 枪耦合过程的影响，并不能反映身管真实的内膛损伤形式(如裂纹、烧蚀坑、铬层剥落及磨损等)，且未对内膛损伤对弹头内弹道过程运动姿态、弹头表面形貌等的影响进行深入研究，不能解释寿终身管在弹头初速未出现明显下降情况下精度就已不满足指标要求的现象。

为分析某大口径机枪真实内膛损伤情况下，不同寿命阶段枪管内膛损伤对弹头挤进过程的影响，本文基于枪管寿命试验获得的不同寿命阶段枪管内膛的损伤数据，建立了各阶段损伤枪管内膛的三维模型并对其进行了精确的网格划分。采用有限元分析软件Abaqus建立了挤进过程的热力耦合有限元分析模型，考虑内膛损伤导致的弹后空间变大，并通过编写弹底压力推力子程序(VUAMP)实现了内弹道方程组和弹头挤进过程的耦合求解。研究并得到了枪管在4个寿命阶段、不同的内膛损伤对弹头挤进过程中挤进阻力、运动姿态及被甲表面刻痕形成的影响规律。

1 挤进过程有限元模型的建立

1.1 基本假设

1) 弹头各部分材料为各向同性材料，比热容、导热系数等热物理性能参数随温度变化而变化；

2) 忽略枪管变形，假设枪管为刚体；弹头材料考虑塑性变形和损伤失效，其屈服强度服从Mises屈服准则；

3) 不考虑枪管后坐，忽略弹头前端空气对弹头运动的影响；

4) 不考虑弹头对流换热和辐射放热。

1.2 有限元网格

1.2.1 枪管与弹头有限元网格

在基于试验获得的内膛损伤数据基础上建立弹- 枪三维模型如图1所示。内膛部分由弹膛、坡膛及线膛组成，弹头由铜被甲、铅套、钢芯及头部填充物组成，初始状态下弹头和坡膛间有一定的间隙，弹头走过一段自由行程后，弧形部与坡膛接触开始挤进过程。

对枪管和弹头进行必要的简化后利用Hyper-Mesh软件对枪管和弹头进行六面体网格划分，如图2所示。枪管及弹头均采用C3D8RT三维八节点热力耦合单点积分单元，由于要准确地还原内膛损伤，必须对损伤处网格进行加密，导致局部很小的网格尺寸，若采用显式算法求解动力学方程，其稳定时间步长也会很小，因此为了节约计算成本，对含内膛损伤的枪管进行网格划分后，将枪管设定为刚体，并固定在空间一定位置处。对弹头圆柱部网格进行局部细化，多次计算结果表明圆柱部网格尺寸为0.1 mm时，可以在不降低计算精度的前提下缩短计算时间，最终弹头总网格数为463 175个。

1.2.2 材料模型

被甲在挤进线膛过程中出现高应变率、材料温度升高、热软化、应变强化等一系列复杂的非线性力学形态，故本文对有较大塑性变形的被甲和铅套材料采用能描述材料热黏性行为的Johnson-Cook本构模型[12]：

(1)

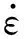
材料有塑性变形时，以等效塑性临界应变εf作为损伤的判活依据：

(2)

式中：D1～D5为材料断裂失效参数；σ*为应力三轴度。

采用线性损伤演化规律描述材料刚度下降，材料累积损伤参数为

(3)

式中：D为材料内单元的损伤值，当单元损伤值D=1时，单元失效失去承载能力并从仿真中删除；Δε为等效塑性应变变化量。

1.2.3 接触算法及边界条件

弹头被甲与枪管内膛间的接触设定为基于罚函数法的通用接触，基于文献[13]中所述，对于高速、高压挤进过程，动摩擦系数应不大于0.02，本文取动摩擦系数为0.01. 弹头底部加以压力载荷pd，载荷值来自于内弹道方程的计算，并由推力子程序VUAMP施加于弹尾。边界条件为枪管和弹壳的全自由度约束。

1.3 热力耦合模型

文献[11，14]研究发现，由于温度升高引起的弹头被甲材料变软导致的弹头内弹道性能(挤进阻力、膛压、弹头初速等)的变化不可忽略。因此本文建立的有限元分析模型为考虑弹头被甲材料塑性变形热Qε及被甲与枪管内膛间摩擦生热Qf导致的被甲材料温度改变的热力耦合模型，二者引起的温度改变量分别为Tε、Tf. 由摩擦热和塑性变形热引起的温度改变如下：

(4)

式中：ρj和cj分别为被甲材料的密度和比热容；σj和εj分别为被甲的应力和塑性应变；β为塑性热转化系数，一般为0.85～0.95，本文取β=0.9.

热量由弹头表面向内传导，采用三维非稳态、变物性热传导微分方程：

(5)

式中：T为弹带材料温度；kX、kY、kZ分别为3个方向的热传导系数；Q为内热源，一般指塑性热。

2 含内膛损伤枪管有限元模型的建模方法

枪管内膛损伤的主要形式有：裂纹、烧蚀坑、镀层剥落及内膛表面磨损。其中：内膛表面磨损会使枪管对弹头的导向及导转作用减小，使得弹头在内弹道过程中扰动增大，导转力减小；裂纹、烧蚀坑等一方面会对弹头挤进及沿膛运动的稳定性产生不利影响，另一方面也会影响弹头嵌入膛线过程中被甲表面刻痕的形貌，严重时甚至会划伤被甲材料，破坏其表面完整性，导致弹头气动性能发生改变。在上述因素的综合影响下，随着射弹量的增加弹头出膛口时的初始扰动及气动性能均与从新枪管中射出的弹头状态有较大差异，最终导致了枪管寿终。

针对某大口径机枪进行的大量寿命试验表明：枪管内膛损伤的形式及分布规律随射弹数的增加表现出极大的规律性[1]，这为使用数值方法模拟不同寿命阶段枪管的挤进乃至整个内弹道过程提供了依据。

通过对枪管内膛直径进行测量，获得了4支不同射弹量的枪管阳线直径沿枪管轴向分布情况如图3所示。射击试验中通过内窥观测得到的枪管坡膛处损伤主要有裂纹、烧蚀坑及铬层剥落，4支枪管坡膛处损伤形式相同，区别在于损伤的严重程度及分布位置有所不同。以射弹量800发的枪管为例，其坡膛处损伤情况内窥图如图4所示，对图4中3种主要的内膛损伤形式分别划分网格如图5所示(图5同时也是射弹数800发枪管的网格划分图)。

以射弹数800发(寿命前期)的枪管为例，分析其有限元模型的建模方法：首先根据图3中试验测得的枪管内膛直径数据建立其三维模型并划分网格；然后根据由试验获得的坡膛部位内窥照片及视频所得到的坡膛段损伤分布规律及严重程度在内膛预置不同数量及分布位置的损伤，即可建立该寿命阶段含内膛损伤枪管的有限元模型。由于不同射弹量的枪管坡膛处损伤形式相同，因此同理可以由图3中其他寿命阶段枪管内膛阳线直径沿轴向分布情况，结合已由试验获得对应射弹量下的内膛形貌特征，建立其他各寿命阶段的枪管有限元模型。

3 内弹道过程耦合计算

本文采用VUAMP子程序的方法，将内弹道方程的求解和弹头运动过程耦合，能够更好地获得内膛有损伤时弹后的膛压数据，提高计算结果的准确度。实现过程如下：使用Fortran语言编写内弹道方程的VUAMP子程序，子程序根据t时刻的火药已燃相对厚度zt等内弹道参数计算得到该时刻弹底压力pd,t，并将弹底压力传入有限元软件中，弹头在pd,t作用下沿膛线向前运动，Δt时间后有限元软件将t+Δt时刻的弹头运动相关参数传回VUAMP子程序，由子程序计算得到此时的弹底压力pd,t+Δt并再次传入有限元软件，对弹头运动参数进行求解。如此往复循环直至弹头出膛。

3.1 基本假设

内弹道方程组满足以下基本假设：

1)火药燃烧服从几何燃烧定律；

2)火药燃烧在平均压力条件下进行；

3)火药燃烧速度与压力呈指数关系；

4)火药燃烧期间和燃烧结束后，火药燃烧生成物始终保持不变，即把火药力f和火药气体余容α当作常量处理。

3.2 内膛磨损导致弹后空间增加的计算

枪管内膛有损伤后，弹后空间会比初始枪管有所增加，并随着弹头沿枪管轴线向前运动，弹后空间的增加量也在不断增加。在弹头运动dt时间内，弹头向前运动ds距离，t时刻时弹尾位置处枪管内膛截面积增加量为ΔS，故弹后空间增加量可以表示为

dV=ΔSds,

积分得到：

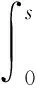
(6)

式中：ΔV为弹后空间增加量；N、K、ΔR分别为膛线条数、阳线角度系数、阳线半径增量[11]。

由于阴线磨损量较小且不易测量，以及由裂纹、烧蚀坑等引起的弹后空间变化很小，本文仅考虑由于阳线磨损导致弹后空间的增大。使用复合辛普森公式求解该积分项以便于编程计算，并将结果加入内弹道方程的弹后空间项中。

3.3 内弹道方程组

对经典内弹道方程组进行改写，考虑挤进过程及由于内膛损伤导致弹后药室容积的增加，并将次要功系数具体为各项能量的形式，同时为便于使用FORTRAN编程，将内弹道方程写为1个主要方程和4个辅助方程的形式，采用4阶龙格- 库塔法求解(7)式中的主要方程得到火药已燃相对厚度z，然后由辅助方程(8)式计算得到膛内平均压力p，根据文献[15]中弹底压力与膛内平均压力的转换公式，计算得到弹底压力pd.

(7)

式中：u1、e1、n1分别为火药燃烧速度系数、火药弧厚及燃速指数；ω为装药量；mb、S分别为弹质量和无损伤线膛的截面积；ψ为火药已燃百分比；θ为热力指数；v为弹头速度；s、Lψ分别为弹头轴向行程、药室容积缩径长；Eq为挤进过程中的总次要功。

辅助方程：

(8)

式中：χ、λ、μ为火药形状特征量；Er、Ef、Eε、Em分别为挤进过程中的弹头旋转动能、摩擦耗散能、弹塑性应变能及火药气体运动功。

综上所述，挤进过程内弹道方程和有限元程序的耦合计算流程设计如图6所示。

4 有限元模型验证及结果分析

本文对某大口径机枪射弹数分别为0发(无损伤)、1 400发、3 000发、6 000发(寿终)的枪管建立了上述弹- 枪耦合有限元模型，对弹头挤进含内膛损伤枪管的过程进行了分析。为便于叙述，将射弹量0发、1 400发、3 000发、6 000发的枪管分别编号为1号、2号、3号、4号枪管。

4.1 模型验证

为了验证所构建有限元模型的准确性，本文将4支枪管弹- 枪耦合模型的内弹道计算结果和试验结果进行了对比。对于无损伤枪管，有限元模型计算得到的内弹道过程最高膛压为328 MPa、弹头出膛口时速度为806 m/s、挤进阻力最大值为10 954 N，与试验测得的最高膛压平均值320 MPa相比升高了2.5%、与平均实测初速800 m/s相比升高了0.75%，与静态挤进试验测得最大挤进阻力12 000 N相比降低了8.7%，其中挤进阻力降低较多是因为高速高压动态挤进过程的摩擦系数比静态挤进试验低[13]。此外，还将理论计算得到的4支枪管弹头初速与试验值进行了对比，如表1所示。从表1可以看出，各枪管发射弹头初速的计算值与试验值误差较小。综上所述，本文建立的弹- 枪耦合有限元计算模型是合理与准确的。

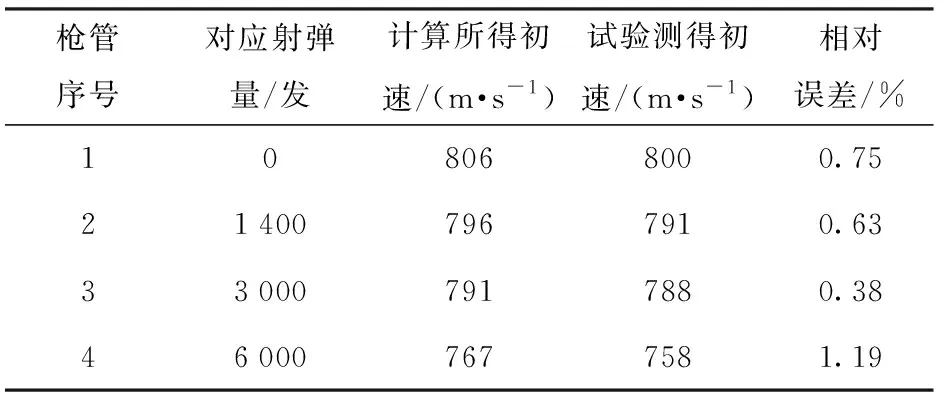
表1 弹头初速对比

4.2 内膛损伤对弹头被甲表面形貌的影响

弹头表面形貌和运动姿态综合影响了弹头外弹道性能，决定了武器射击精度，对挤进过程，尤其是枪管内膛不同程度损伤形貌下的挤进过程进行分析，可以从根源上分析武器精度不达标而寿终的机理。

由装配条件及弹- 枪结构可知，整个挤进过程对应的弹头轴向行程s为5～50 mm，图7～图9所示分别为弹头被甲挤进4支枪管过程中对应弹头轴向行程分别为10 mm、30 mm、50 mm时弹头圆柱部的von Mises应力云图(右侧为弹头头部)，也同时可以间接反映被甲的变形状态。图7对应弹头挤进的初期(被甲刚开始嵌入膛线)，从中可以看出随着枪管内膛磨损量的增加，相同轴向位移时弹头表面刻痕不断变浅，即弹头挤进起始位置向枪管口部方向移动，导致了挤进前弹头自由运动行程(弹头初始位置到初始挤进位置之间的轴向距离)增加。自由行程的增加会使弹头在脱离弹壳后缺少轴向定位，弹头运动的不确定性增大，弹头扰动增大，对弹头挤进过程中的运动姿态及表面形貌的规则性及完整性均会产生不利影响。图8、图9分别为弹头刚全部嵌入坡膛膛线以及弹头完全嵌入全深线膛的时刻，从图8(a)、图9(a)可以看出，弹头挤进无损伤枪管时，其表面刻痕的对称性及表面的完整性保持得较好，表现为除规则由阳线形成的刻槽外，其他位置无不规则刻痕形成，且导转侧与非导转侧处刻痕宽度、深度也基本相同，以及弹头所受应力值及应力的轴向梯度也较小。随着内膛损伤的不断发展，阳线高度及宽度随着磨损及铬层的剥落不断减小，使得被甲表面刻槽的宽度、深度及长度都在不断减小，如表2所示，这会使得弹头所受导转力及转速随损伤的发展而不断降低，不利于弹头飞行稳定。

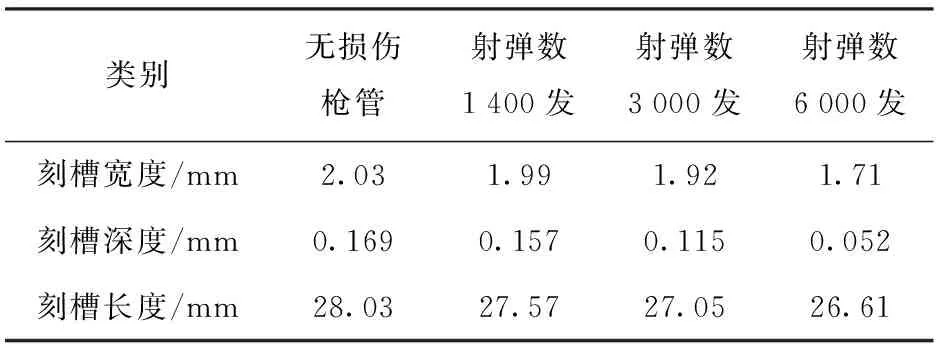
类别无损伤枪管射弹数1400发射弹数3000发射弹数6000发刻槽宽度/mm2.031.991.921.71刻槽深度/mm0.1690.1570.1150.052刻槽长度/mm28.0327.5727.0526.61

此外，由于阳线导转侧损伤程度较非导转侧更为严重，使得弹头在这两个位置处刻槽的形状随射弹数增加表现出明显的非对称性，如图9(b)、图9(c)、图9(d)所示。结合图9(b)、图9(c)可以看出：阳线表面不规则的铬层剥落及烧蚀坑会使得被甲刻槽的中间出现不规则的刻痕，并随着损伤的扩展而扩展；而在枪管寿命末期，由于阳线表面铬层已经基本全部剥落，阳线表面被磨损得比较规则，被甲的刻槽中间反而不会出现明显的不规则刻痕，如图9(d)所示。

4.3 内膛损伤对弹头挤进过程运动姿态的影响

除弹头表面形貌外，内膛损伤也会对弹头挤进过程的运动姿态产生较大影响，如弹头质心在垂直枪管轴线平面内的摆动位移、弹头轴线与枪管轴线之间的夹角(摆动角)等。弹头挤进4根枪管过程质心在垂直枪管轴线平面内的竖直和水平偏移量如图10所示。

从图10可以看出：挤进初始阶段，对应图10中Ⅰ区，弹头运动完自由行程刚开始挤进，此阶段由于弹头运动缺少约束且冲击较大，弹头挤进4支枪管时质心偏移量均较大，随着弹头在枪管约束下逐渐归正，质心偏移量均在逐渐减小，枪管内膛损伤越严重，弹头完全归正所需的弹头轴向行程越长；Ⅱ区为平稳挤进阶段，此阶段弹头已大部分挤进膛线，弹头运动较平稳，对比4条曲线的质心偏移量可以明显发现，随着枪管内膛损伤的扩展，弹头质心在垂直枪管轴线平面内的偏移量呈明显的增加趋势，弹头完全挤进膛线时，2号～4号枪管对应的质心总偏移量，即图10中挤进终了时刻(对应曲线终点位置)弹头质心在竖直方向和水平方向偏移量的矢量和，分别为1号枪管对应总偏移量的2.90倍、3.01倍、3.61倍，内膛损伤对弹头质心运动姿态的影响十分严重。

枪管内膛损伤也会对弹头轴线与枪管轴线的夹角(即摆动角)产生较大影响，而弹头出膛口后的摆动角和弹头表面形貌综合影响了弹头外弹道过程的气动参数，是影响弹头飞行稳定性和自动武器精度的决定性因素。本文在弹头质心建立局部坐标系，并在质心局部坐标系和地面坐标系之间建立无自由度约束的连接器，获得了弹头挤进4支枪管过程中弹头轴线与枪管轴线的夹角随弹头挤进过程的变化情况，并将其分解到过枪管轴线的竖直平面和水平平面内，分别对应为铅垂摆动角与侧向摆动角，如图11所示。从图11中可以看出：在挤进的初始阶段，弹头由于刚嵌入膛线，存在着动态冲击并且缺少内膛的有效约束，两个方向的摆动角均较大；随着弹头不断向前挤进，摆动角呈下降趋势，且内膛损伤越严重的枪管，弹头摆动角下降得越慢。在挤进的中后期，弹头运动趋于平稳，摆动角均较小，且随着枪管射弹数的增加，两个方向摆动角均呈增加的趋势。与图10不同的是，图11中Ⅲ区对应的挤进末期内，4支枪管的摆动角均较之前开始增加，这是因为在挤进末期，弹头已经绝大部分完成了挤进并开始了沿线膛运动过程，弹头所受轴向阻力迅速下降，弹头轴向速度及转速开始快速上升，使得弹头轴向运动的摆动量增大，这与文献[8]中对内弹道时期弹头摆动角变化规律的研究结果是一致的。

4.4 内膛损伤对弹头挤进阻力的影响

(9)

图12为弹头挤进4支枪管过程的挤进阻力随弹头轴向位移的曲线，弹头挤进每支枪管的最大挤进阻力及此时对应的弹头轴向位移列于表3中。结合图12及表3可以发现：挤进阻力的峰值出现在弹头完全挤进全深膛线之前，这是因为随着弹头被甲不断挤进膛线，被甲塑性变形量不断增大，挤进阻力迅速上升，在塑性变形量最大时挤进阻力达到峰值，此后随着塑性变形量的减小而降低，其变化规律与文献[7]关于挤进阻力的变化规律研究结果相符；弹头挤进过程挤进阻力随枪管射弹数增加而不断下降，且挤进阻力达到峰值时弹头轴向位移在不断增加，这是因为随着射弹数的增加，内膛磨损不断加重及坡膛处铬层逐渐剥落均导致了坡膛阴阳线直径的扩大，使得被甲材料完全嵌入膛线时的塑性变形量降低，达到相同塑性变形量时的弹头轴向位移增加，这与文献[16]中不同坡膛角下的挤进阻力变化规律相似。

5 结论

本文针对大口径枪械枪管寿命较短这一严重问题，在试验基础上建立了弹头挤进不同射弹数枪管的数值分析模型，研究了内膛损伤对弹头表面形貌及运动姿态等的影响规律，得出以下结论：

1)内膛损伤会显著影响弹头表面形貌及运动姿态等与外弹道性能紧密相关的参数，弹头内弹道过程扰动增加，弹头所受导转力和转速下降以及气动力参数发生改变等是导致弹头外弹道飞行稳定性降低，横弹孔率上升，进而导致枪管寿终的主要原因。

2)弹头挤进无损伤枪管时，其表面刻痕的对称性及表面的完整性保持得较好，表现为除规则由阳线形成的刻槽外，其他位置无不规则刻痕形成，且导转侧与非导转侧处刻痕宽度、深度也基本相同，弹头所受应力值及应力轴向梯度也较小。

3)随着枪管射弹数增加，弹头挤进后表面形貌的改变明显，表现为被甲表面刻槽的宽度、深度及长度在不断减小；导转侧与非导转侧刻槽的形状呈明显的非对称性；被甲表面除阳线形成的刻槽外还出现了不规则分布的刻痕。

4)弹头挤进过程质心的非轴向位移及弹头摆动角随着挤进过程弹头的归正而逐渐减小；随着射弹数增加，挤进过程弹头归正所需要的弹头轴向行程以及归正后的非轴向位移量、摆动角等都在增加。

5)随着枪管射弹数增加，挤进过程挤进阻力不断下降，且挤进阻力达到峰值时弹头轴向位移在不断增加。