圆周运动“不脱离”问题的多题一解
邵贝


摘 要:分析竖直平面内圆周运动“不脱离”问题的几种类型。注意区分小球所处的物理情境,找到“力学最高点”和“力学圆心等高点”,是解决此类问题的关键,真正做到“多题一解”。
关键词:多题一解;圆周运动;不脱离
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2018)10-0035-4
1 情形一:大小不等的两圆拼接
例1 如图1所示,竖直平面内有光滑圆轨道ABCDE,ABC为半径为R1的半圆,CDE为半径为R2的半圆轨道(R1大于R2)。要使质量为m的小球在圆轨道内侧运动不脱离,在最低点A的速度v0为多少?
解析 (1)情况一,小球能做完整的圆周运动,到达最高点C,如图2所示。在此处,小球受重力和弹力,对于ABC半圆轨道而言:
在C处,要同时满足两个半圆轨道运动情形,而R1大于R2,所以在最高点C,速度v要大于等于v1(v>v1时,在最高点轨道对小球产生压力)。
从最低点A到最高点C用动能定理:
2 情形二:匀强电场和重力场中的圆周运动
2.1 匀强电场方向竖直向下
例2 如图4所示,竖直平面内有光滑圆轨道ABCD,半径为R,处在竖直向下的匀强电场中,电场强度为E。有一个质量为m,带电量为+q的小球,想让小球在运动过程中不脱离圆轨道,小球在最低点速度应为多少?
2.2 匀强电场方向水平向右
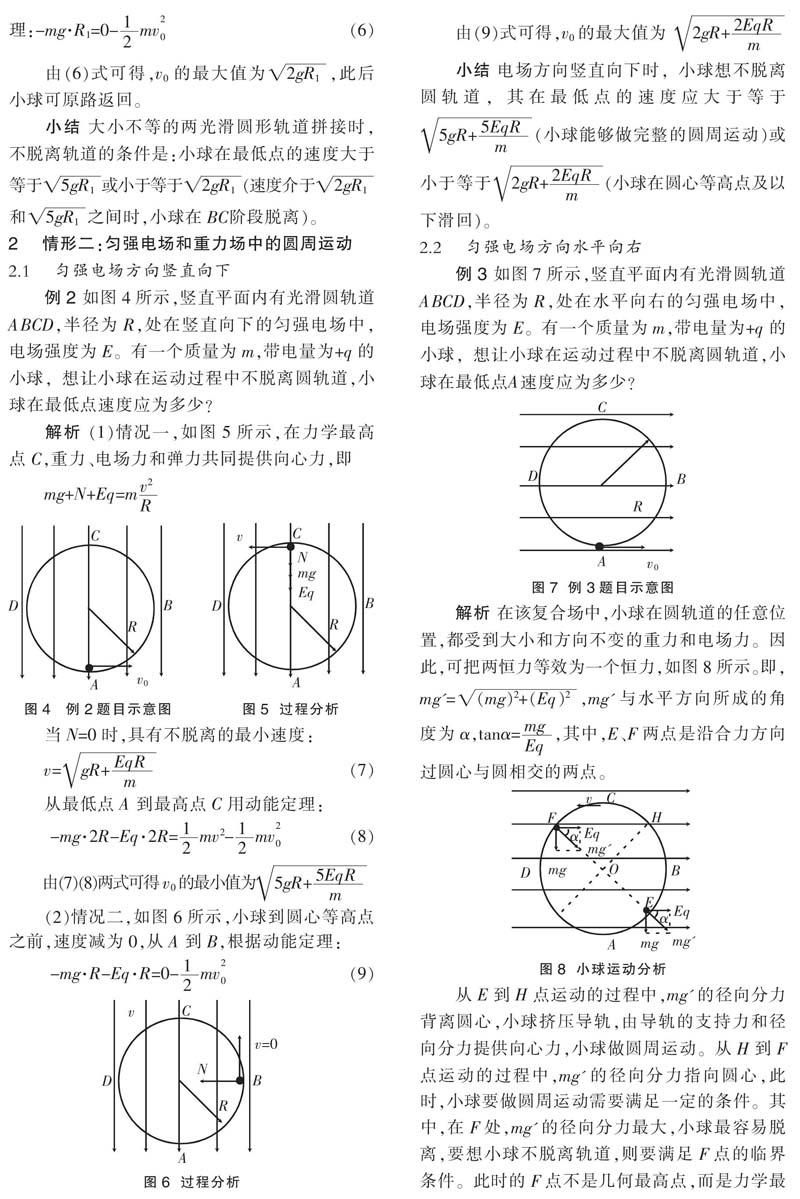
例3 如图7所示,竖直平面内有光滑圆轨道ABCD,半径为R,处在水平向右的匀强电场中,电场强度为E。有一个质量为m,带电量为+q的小球,想让小球在运动过程中不脱离圆轨道,小球在最低点A速度应为多少?
从E到H点运动的过程中,mg'的径向分力背离圆心,小球挤压导轨,由导轨的支持力和径向分力提供向心力,小球做圆周运动。从H到F点运动的过程中,mg'的径向分力指向圆心,此时,小球要做圆周运动需要满足一定的条件。其中,在F处,mg'的径向分力最大,小球最容易脱离,要想小球不脱离轨道,则要满足F点的临界条件。此时的F点不是几何最高点,而是力学最高点,E为力学最低点。
3 情形三:匀强磁场和重力场中的圆周运动
例4 如图11所示,竖直平面内有光滑圆轨道ABCD,半径为R,处在垂直纸面向外的匀强磁场中,磁感应强度为B。有一个质量为m,带电量为+q的小球,想让小球在运动过程中不脱离圆轨道,小球在最低点速度应为多少?
解析 在此过程中,洛伦兹力始终背离圆心,从A到B,重力的径向分力也背离圆心,挤压导轨,使小球顺利做圆周运动。从B到C,重力的径向分力指向圆心,在C处达到最大值,而在此处小球所需的向心力最小,因此,在此处最易脱离。
(1)情况一,如图12所示,在力学最高点C,重力、弹力和洛伦兹力共同提供向心力,即
4 小 結
以上几种竖直面内圆周运动“不脱离”问题,解决的关键都在于找到力学最高点和力学圆心等高点,而并非几何最高和圆心等高点。所以,看似情境不同,但解决的方式是一致的,先受力分析,找到力学最高和圆心等高点,再列向心力表达式和动能定理,最后求得结果。所以,在今后的学习中,也要对各类题型多加总结,深入剖析,做到“多题一解”。
参考文献:
[1]曾文,周朝彪,桂朝觐.竖直平面内圆周运动的临界问题分析[J].考试周刊,2015(86):130.

