二维电流场的保角变换法研究及其可视化
王福谦, 刘伟岐, 殷 勇
(西南交通大学 希望学院 基础部, 四川 成都 610400)
0 引言
二维电流场为电流场的较为简单的情形,为恒定电场的研究内容之一。有关教材对二维电流场的分布一般仅作定性分析,没有给出定量的计算。为此,本文利用保角变换法研究二维电流场的分布,给出其复势函数,并通过数学软件Matlab绘制出其电流线和等势线图,实现其电流场分布的可视化。
1 上半平面电流场的复势函数
首先考虑w平面上v=0和v=π之间的导体带上有一恒定电流注入,电流的方向垂直于导体带边缘.设注入的电流强度为I,则向左和向右沿导体带流动的电流强度均为I/2,如图1所示(由软件Matlab绘制)。
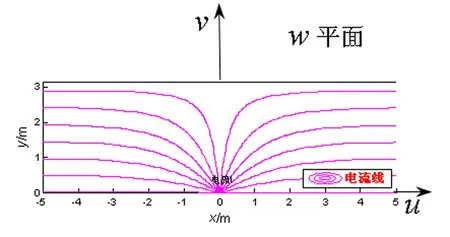
图1 由导体带边缘注入的电流
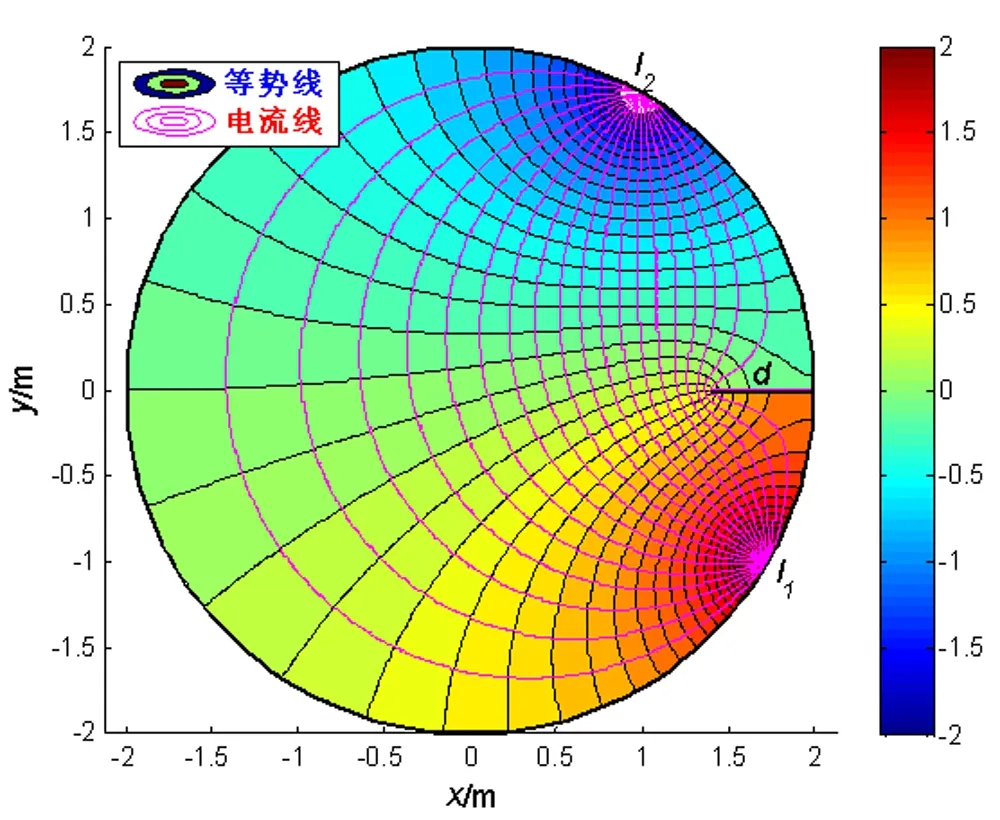
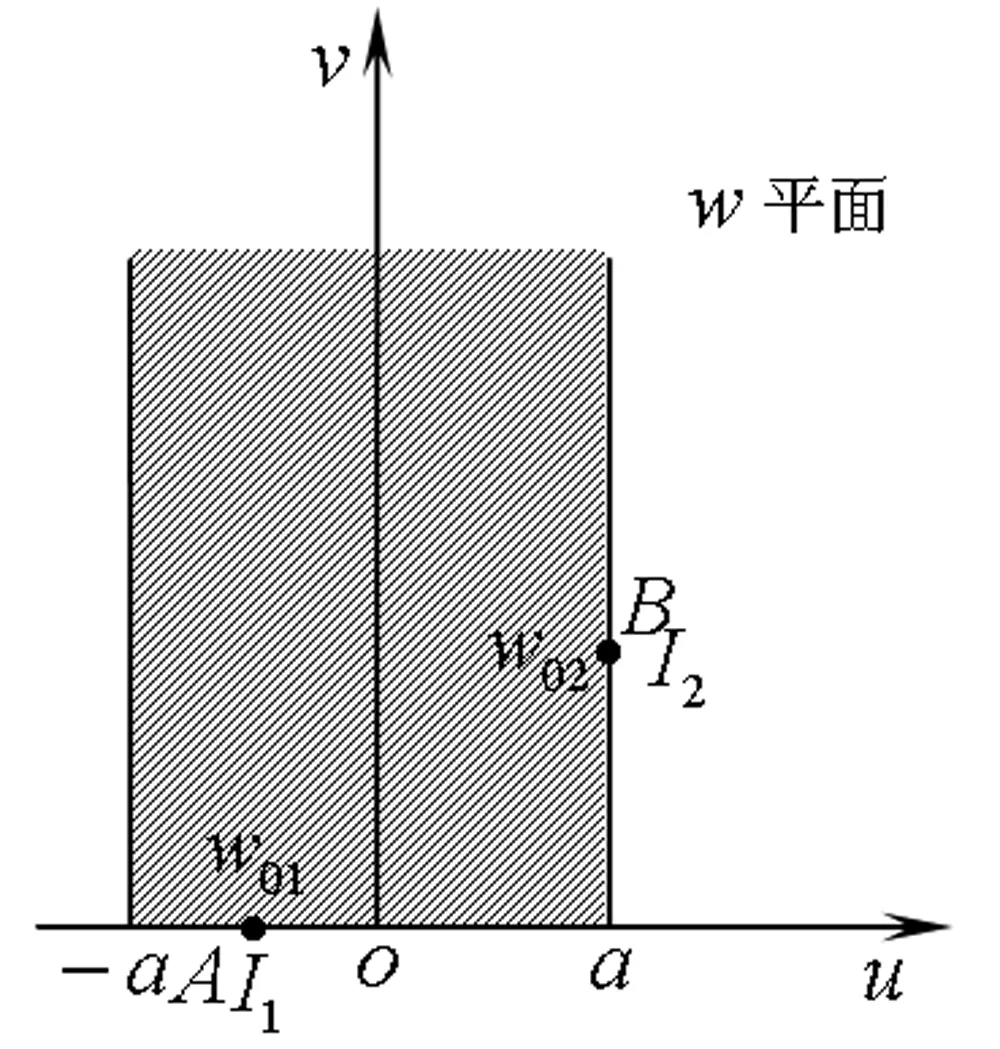
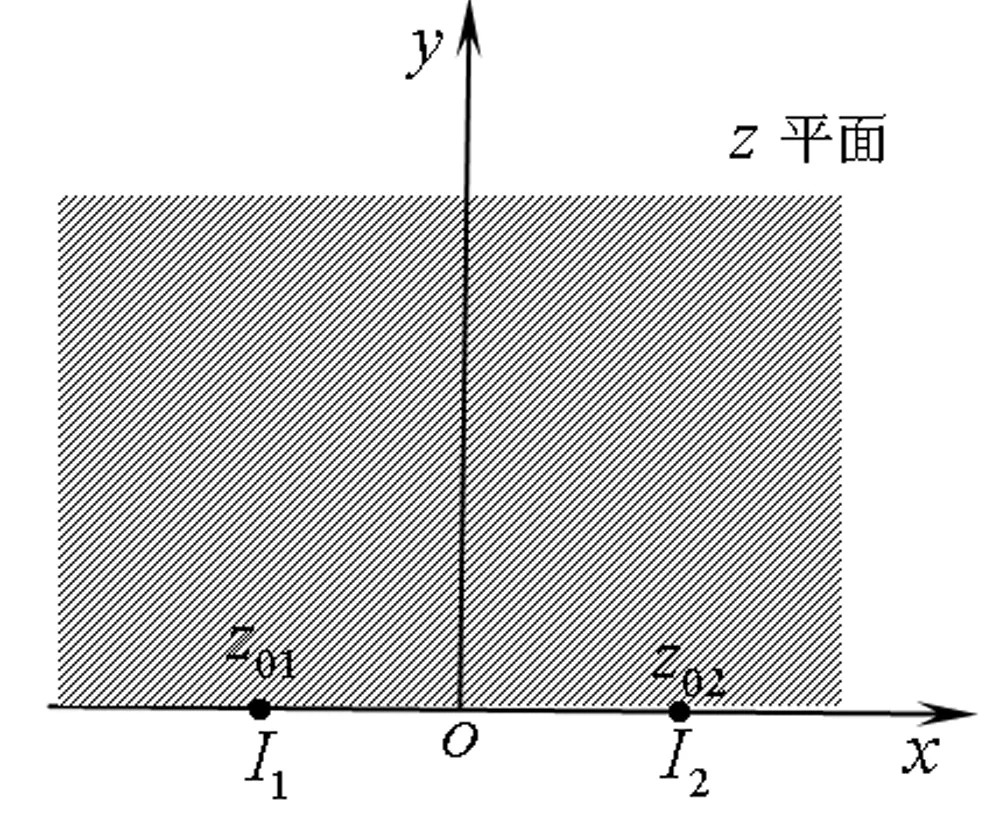
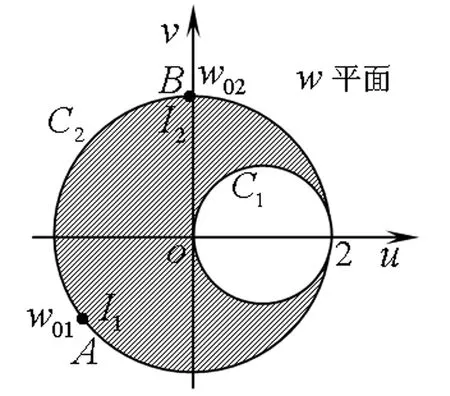
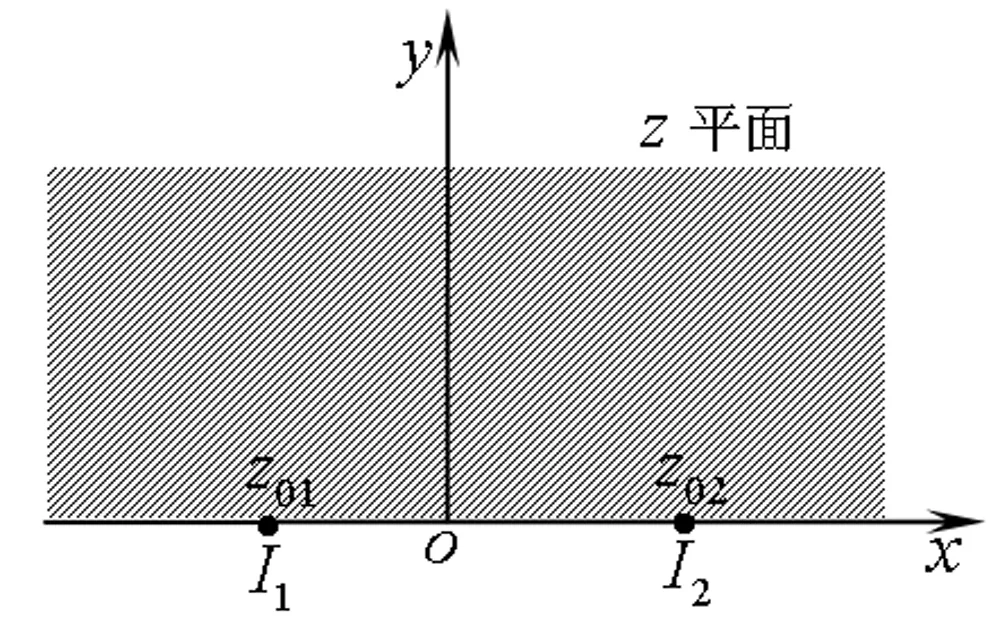
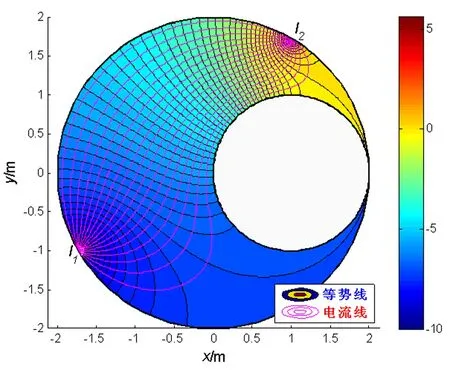
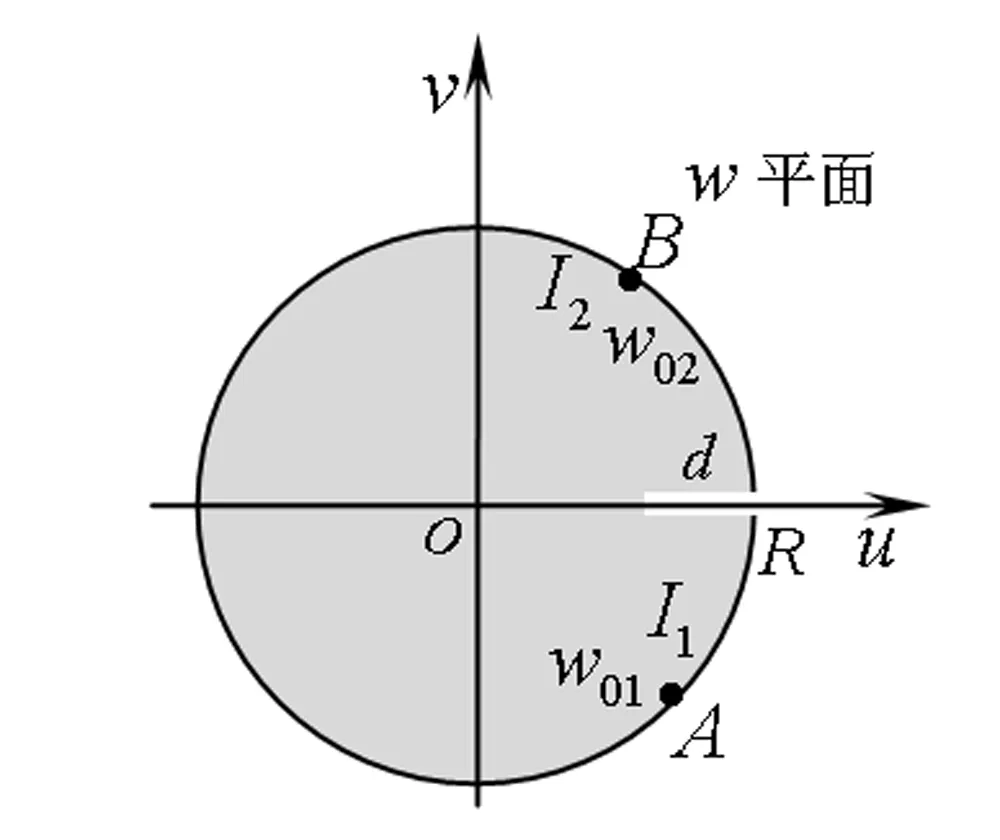
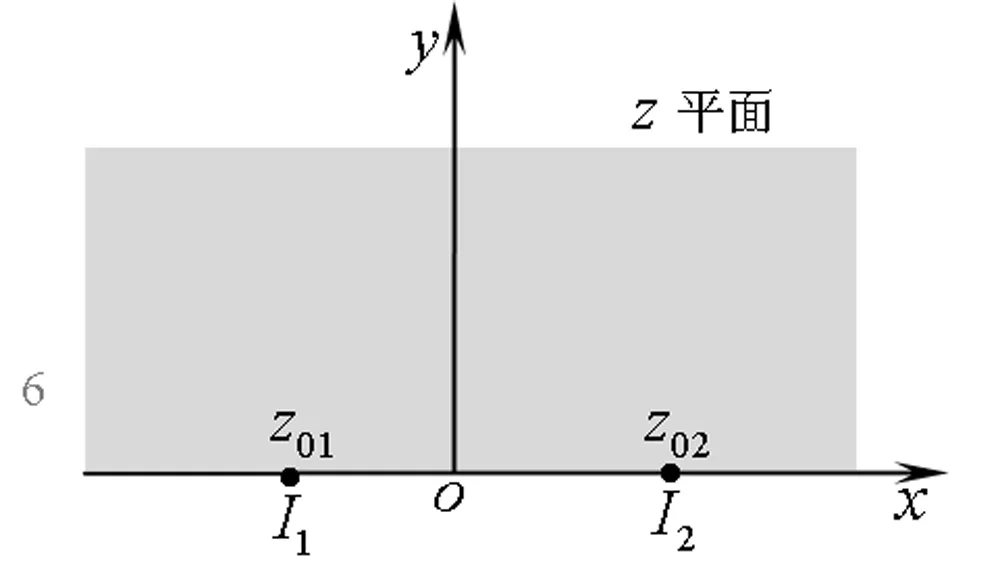
保角变换w=lnz将z平面的上半部分y>0映射为w平面上的带形区域0 z=ew (1) 则将带形区域映射为上半平面.通过变换函数(1),u轴的像为x轴的正半轴,直线v=π的像为x轴的负半轴,带形区域的边界映射为上半平面的边界。在z平面上点z=1处注入电流相当于在w平面上点w=0处注入电流,当Rew→-∞时,w的像点趋于z=0,在标记点电流强度为I/2的电流流出,对应于带形区域电流向左流向无限远处,而在半无限大平面电流向无限远处流动,则应于带形区域电流向右流向无限远处。所以,上半平面上电流的流动一定满足:当z绕z=1从位置z=x0移到位置z=x1时,其值增加I;当z绕原点以相同的方式移动时,其值增加I/2,如图2所示。 图2 带形区域映射为上半平面 满足上述要求的电流函数为 (2) 式(2)在z平面的上半平面调和,为如下式(3)的电流场的复势函数的虚部。 (3) (4) 显然,如果通过适当的保角变换z=f(w),能够将w平面上边界较复杂的二维电流场区域,映射为z平面上半平面,则式(4)可表达为 (5) 当导体板通有多个电流时,上式可改写为 (6) 利用式(5)、(6),便可求得边界较为复杂的二维电流场区域内的电流分布。 如图3所示,半无限长的条形导体带在其边缘A、B两位置处接有电流I1和I2,且I1=-I2。取半无限长导体板所在的平面为w平面。为了研究半无限长导体带上的电流场,需将w平面上的半无限长条形区域变换为z平面的上半平面,如图4所示,其变换函数为 (7) 图3变换前的半无限条形域-a 图4变换后的上半平面Imz>0及线电流的位置 将式(7)代入式(6),即得半无限长的条形导体带上电流场的复势函数为 J(u,v)= (8) 因为式(8)为半无限长的条形导体带上电流场的复势函数,故对其取实部和虚部,可得到其电势和电流密度函数。 J(u,v)= 因为I1=-I2=1,故上式可简化为 (9) 由式(9),有 (10) 及 j=E-F (11) 式(10)和式(11)分别为半无限长的条形导体带上电流场的电势函数和电流密度函数。 为了给出半无限长条形导体带上电流场分布的直观图像,并验证本文研究结论的正确性,下面通过式(8)利用软件Matlab绘制半无限长条形导体带上电流场的电流线和等势线图(见图5)。图5中的无限长条形导体板的宽度为2a=6 m。线电流I1=I2=-2 A ,其位置分别为w01=-2 m、w02=(3+4i)m。由图5中的场线分布可以看出,靠近导体带边界处,电流平行于边界,即垂直于边界的电流分量为零,而等势线与电流线及导体板边界均垂直,符合电流的分布规律,为预期结果。这也说明本文的研究方法正确,结论可靠。 图5 半无限长条形导体板内的电流场 如图6所示,月牙形导体板在其边缘A、B两位置处接有电流I1和I2,且I1=-I2。取月牙形导体板所在的平面为w平面.为了研究月牙形导体板内的电流场,需将w平面上的月牙形区域变换为z平面的上半平面,如图7所示,其变换函数为函数[2]: (12) 将式(12)代入式(6),即得月牙形导体板上电流场的复势函数为 (13) 图6 变换前的月牙形区域及线电流的位置 图7变换后的上半平面及线电流的位置 若要进一步得到月牙形导体板上电流场的电势和电流密度函数,可对式(13)取其实部和虚部,计算方法与2.1中相同,此处从略。 为了给出月牙形导体板内电流场分布的直观图像,并验证本文研究结论的正确性,下面通过式(13)利用软件Matlab绘制月牙形导体板内电流场的电流线和等势线图(见图8)。线电流I1=-I2=-3.5 A ,其位置分别为 由图8中的场线分布可以看出,靠近月牙形导体板边界处,电流平行于边界,即垂直于边界的电流分量为零;而等势线与电流线及导体板边界均垂直,符合电流的分布规律,为预期结果。这也说明本文的研究方法正确,结论可靠。 如图9所示,开有狭缝的圆形导体板在其边缘A、B两位置处接有电流I1和I2,且I1=-I2。取开有狭缝的圆形导体板所在的平面为w平面。为了研究开有狭缝的圆形导体板内的电流场,需将w平面上的开有狭缝的圆形区域变换为z平面的上半平面,如图10所示,其变换函数为函数[3] (14) 图8 月牙形导体板内的电流场 图9变换前的开有狭缝的圆形导体板及线电流的位置 图10变换后的上半平面及线电流的位置 (15) 若要进一步得到开有狭缝的圆形导体板上的电流场的电势和电流密度函数,可对式(15)取其实部和虚部,计算方法与2.1中相同,此处从略。 本文将理论分析与计算机数值模拟相结合,研究了边界形状复杂的二维电流场,给出了电流场复势函数数的解析解,并利用Matlab软件绘制出了其电流线和等势线,实现了电流场分布的可视化,为边界复杂的电流场问题的求解提供了一种思路与方法,可供相关的电流场问题研究借鉴,在教学和科研上具有一定的参考价值。 图11 开有狭缝的圆形导体板内的电流场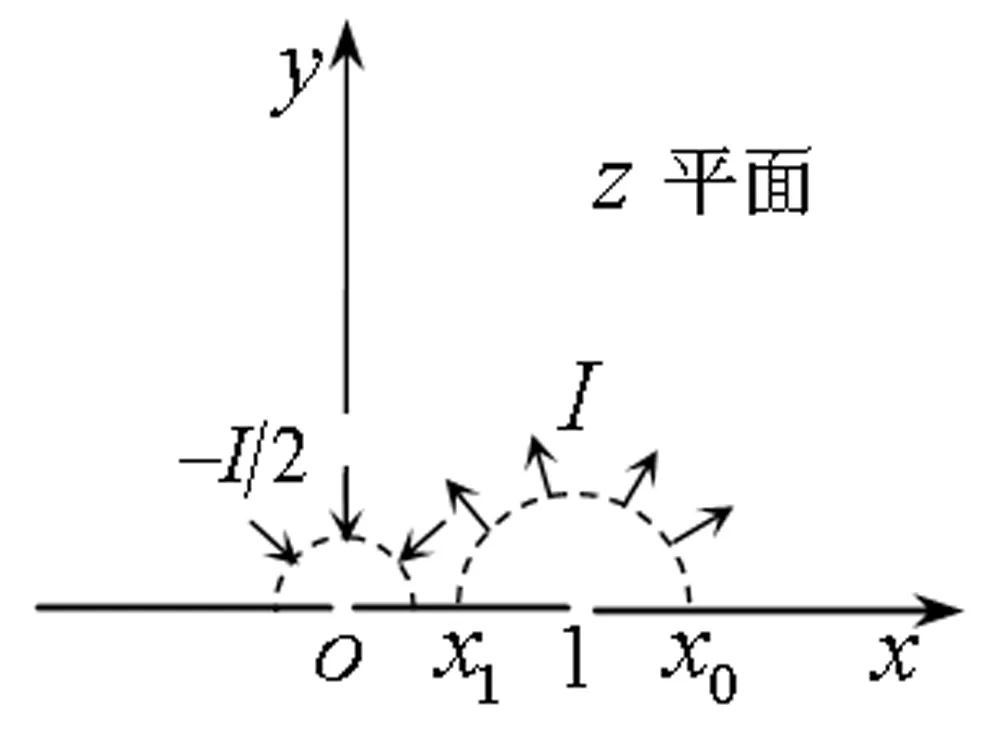
2 平面电流场的求解与可视化
2.1 半无限导体带上的电流场及其可视化
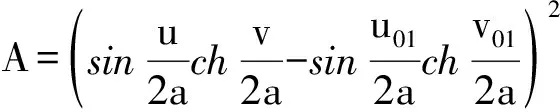
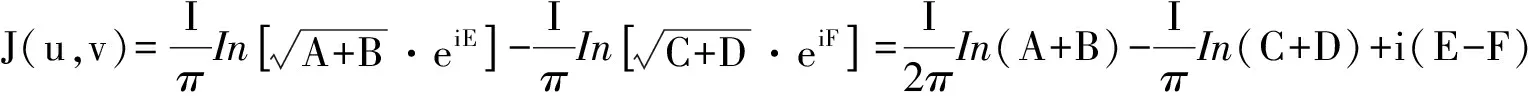

2.2 月牙形导体板上的电流场及其可视化
2.3 开有狭缝的圆形导体板上的电流场及其可视化
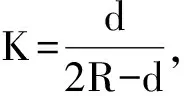
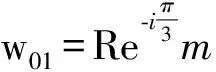
3 结语