半导体设备回转件设计中的动力学问题探究

王勇威，王文丽，黄鑫亮，胡天水，王丽江

(中国电子科技集团公司第四十五研究所，北京 100176)

在半导体加工制造过程中存在大量回转机构，如CMP中的回转工作台和抛光头，多线切割中的刀盘，甩干设备中异形转子等。据有关资料：由于回转构件不平衡引起的机械设备振动约占所有引起原因的30%[1，2]。设备振动问题直接限制了设备的加工精度、可靠性和使用寿命。如果振动过大，很可能引起晶圆破碎，以致生产效率降低，生产成本增加，更为严重的会导致机组发生严重损坏，造成重大事故[3]。因此在设计回转构件过程中必须考虑其转子动力学问题，加工装配完成后还需进行严格的动平衡调整。

1 转子设计中的动力学

1.1 转子系统的受迫振动

所有设备转轴-转子系统可以简化为一个单自由度二阶系统[4]，其模型如图1所示，设偏心质量为m，偏心距为e的旋转系统以角速度ω旋转时，则偏心质量同样以ω作等速圆周运动，它产生的离心力为：

图1 设备简化模型

则引起系统的受迫振动为:

式中：X为系统位移响应；φ为响应与激振力的相位差；λ为频率比；ζ为阻尼比。

由上式可得出减小系统的受迫振动的方法为：减小偏心质量和偏心距，即在固定转速下降低激振力的产生；降低频率比，所设计系统的固有频率应尽量远离工作转速，防止系统产生共振。

1.2 转子临界转速

当转子系统工作转速靠近临界转速时，设备将产生剧烈振动，这是由不平衡离心惯性力引起的振动现象，要避免这一现象的产生，首先应研究转子的临界转速位置。

当转子系统在其临界转速附近运转时，将产生剧烈振动以致损伤机件，这是一种由不平衡离心惯性力引起的共振现象[5]。现用图2竖直单圆盘轴来说明这一现象，转轴只考虑其刚度k忽略其质量，圆盘只计质量m，这种转子模型称为Jeffcott转子。设轴系阻尼为c，圆盘几何中心为A，质心为C，偏心距AC=e。当轴静止时，其轴心线与铅垂线AB重合，当旋转时偏心质量产生的离心惯性力meω2，使轴弯曲离开原位置到达OAB位置，O1为转轴弯曲后AB与圆盘所在平面的交点，则轴动挠度O1A=γ。

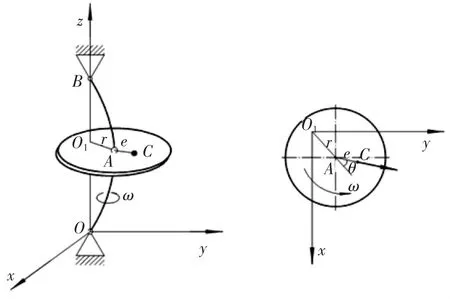
图2 单盘转子的不平衡相应

此时，相对于固定坐标系Oxyz建立一个二阶常系数线性非齐次微分方程：

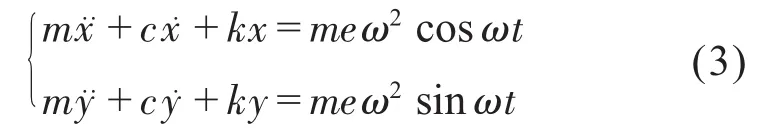
求得其静态解：

其中：

则动挠度：

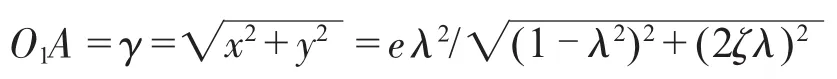
将此关系式无量纲化：

相应r和激励偏心e之间的相位角：

此时转轴做两种运动：一是圆盘自身转动，二是弯曲了的轴绕OAB转动，轴变形呈弓状。此时离心惯性力对支撑产生交变作用而使系统发生振动，其动挠度随转速变化，根据式(5)、(6)可得转子模型的幅频特性和相频特性曲线，如图3所示。

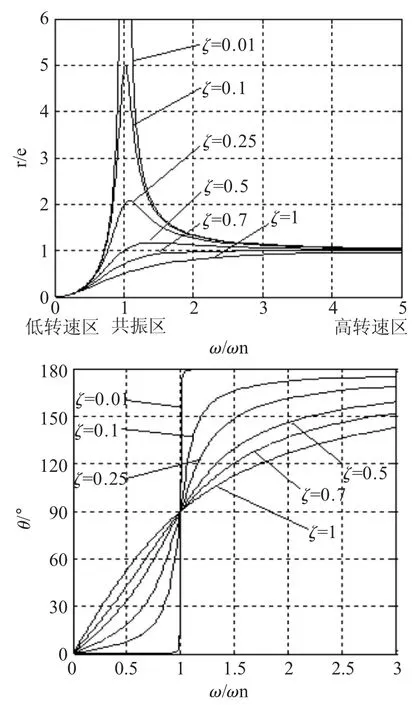
图3 单盘转子的幅频特性和相频特性曲线

由图3得，λ≈1时，转子系统进入共振区，γ/e≫1，转子相应很大，即发生了共振。共振峰的高低与阻尼比ζ有很大关系，若ζ=0，即使e很小，轴的弯曲也会趋于无限大，这样的转速对轴、支撑甚至其他机件产生极大的破坏。

由于转子系统都比较复杂，难以通过简单的公式将固有频率计算出来，现代工程设计中一般通过有限元分析中的模态分析及或者转子动力学专用分析工具得到其固有频率，理论上一个复杂系统会得到无数组模态，我们可只取前几阶或者感兴趣的模态，用来作为优化目标。工程中一般将第一临界转速的70%作为分界点，即工作转速低于此转速为刚性转子，高于此转速便称为柔性转子[7]。

1.3 惯性主轴

在刚体定轴转动时，刚体在转动轴上的动量矩为：

与质点运动相比较，我们把J称为转动惯量，它表示刚体定轴转动惯性的大小。在刚体定点转动时，刚体的动量矩为（其简图如图4所示）：

图4 动量矩简图

在直角坐标系下：

则式8写成矩阵形式：

简写成：

其中：

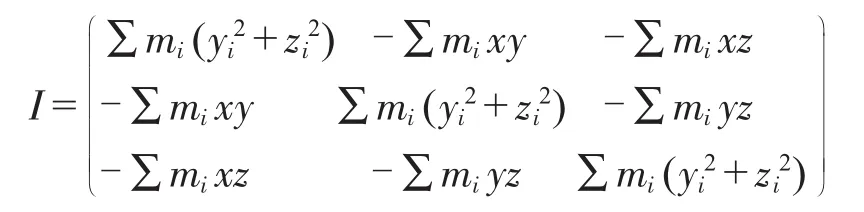
则我们称I为转动惯量张量[6]。惯性张量I是三阶实对称阵，即为正定矩阵。由矩阵论知惯性张量 I有三个实特征值 λ1、λ2、λ3及与之对应的三个正交特征向量 ω1、ω2、ω3，将这些特征向量单位化即为刚体的惯性主轴的方向余弦，而特征值则是分别对应惯性主轴方向的转动惯量[7]。

2 刚性转子设计

由于柔性转子平衡问题较复杂及篇幅限制，本文只对刚性转子的设计作讨论。对于刚性转子即使各部分作用有离心力也不会产生变形，所以转子的质量分布与转速无关而保持不变，这种转子也称为恒态转子，其不平衡形式有3种[8，9]。

（1）静不平衡。转子在轴向的质心分布均匀，且惯性主轴与旋转轴心平行，不平衡离心力系可以合成一个与旋转中心垂直的合力，如图5所示，平衡此类转子只需在合力平面添加一平衡质量即可。

图5 静不平衡

（2）偶不平衡。转子的质心与旋转轴心重合，但惯性主轴与旋转中心相交于质心点，不平衡力系向质心简化智能得到一个合力偶，如果平衡此类转子需要在质心两侧合适位置同时施加平衡质量，以平衡力偶，如图6所示。

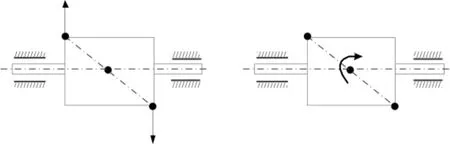
图6 偶不平衡

（3）动不平衡。转子质心与旋转轴心不重合，惯性主轴与旋转轴心交叉但不共面。不平衡力系向质心简化可得一个合力和一个力偶，如图7所示，显然，它是静不平衡和偶不平衡的综合。在下节中将以动不平衡为例，介绍刚性转子的平衡方法。

图7 动不平衡

综上所述，在设计刚性转子时应在保证质心与旋转中心重合，如果转子由几部分组成，如甩干机转子-片盒系统，应尽量在考虑配合间隙的同时，将组合质心与旋转轴心重合。由于大多数转子外形不规则，惯性主轴的计算较复杂，可以利用三维软件中自动求解构件质量属性功能，方便的判断各惯性主轴的方向，只有当所设计转子其中一条惯性主轴与旋转轴重合时，工作过程中才能保证不在其余方向产生力矩分量。

3 转子的动平衡

3.1 不平衡指标量化

所谓平衡就是使转子的质量分布变成完全平衡的一种操作。处于不平衡状态的转子如果从平衡的角度看，可以理解为具有“完全平衡状态+质量偏差”的质量分布转子[9]。考虑上节中转动系统不平衡量产生的离心力：

由于ω为转速，只有系统不平衡质量m，偏心距e为系统的固有属性，所以在转子动力学中将系统不平衡质量m与偏心距e的乘积来表示转子不平衡量的大小，称之为质量矩U，单位为g·mm或kg·m。

另外，质量矩U还可以用系统质量M与其质心到转轴的距离a的乘积表示：

这两个公式在力学上是等价的。在工程应用中应根据实际需要制定经济合理的指标，并根据不平衡指标对转子进行动平衡矫正。

3.2 平衡方法

对于普通的转子而言，需要考虑双面动平衡，即在转子前后两面同时匹配调整质量，来去除转子转动产生的离心力和合力偶。如图8离心惯性力系向质心C简化得到一个力F和一个力偶Mc[8]。

将合力F和力偶Mc向平面Ⅰ和平面Ⅱ简化，通过匹配平面Ⅰ的配重m1和平面Ⅱ的配重m2，来达到整体转子的平衡。

图8 动平衡调整

在将 MC向两个平面分解得两个力和，有

3.3 平衡机平衡

平衡机是平衡转子的机电设备，其操作方法简单规范。可以准确地确定不平衡方位及不平衡量，通过微小的改动便可使转子不平衡量控制在要求的范围内。这种方法适合拆卸容易、高转速、平衡精度要求较高的转子，如多线切割机和内圆切片机主轴系统，图9为内圆切片机刀盘的动平衡机平衡。

3.4 现场动平衡

转子在原安装状态下做平衡工作，称为现场平衡，或就地平衡。与平衡机上的平衡相比，其工作效率不如平衡机，对操作人员的技术水平要求也较高[10]。现场平衡时转子所处的状态就是其工作状态，因此能够保证得到更好的平衡效果。现场平衡方法比较适合于单件的转子和拆装、安装比较困难的场合。图10为甩干机转子到达客户现场后配合动平衡仪的现场动平衡。

图9 刀盘动平衡机平衡

图10 甩干机转子现场动平衡

4 结束语

本文较为系统地阐述了回转设备中转子设计时所涉及的动力学问题，并着重介绍了刚性转子设计时应考虑的质心及惯性主轴等关键部分。通过分析转子平衡所应用的力学模型，为后续实践应用提供了理论依据。对比转子动平衡所采用的动平衡机平衡及现场动平衡特点，为半导体回转类构件动平衡寻找到经济可行的平衡方法。