一种基于SMAFA优化算法的多机电力系统稳定器参数最优设计

詹仁俊



一种基于SMAFA优化算法的多机电力系统稳定器参数最优设计

詹仁俊

（福建水口发电集团有限公司，福州 350000）

传统电力系统稳定器（power system stabilizer, PSS）的性能受自身参数影响较大。为最大限度提高电力系统稳定的性能，当前的研究主要将优化算法用于PSS参数的整定。自适应萤火虫算法（adaptive firefly algorithm, AFA）作为一种新兴的群体智能优化算法，其具有较好的全局搜索能力，非常适用于电力系统优化问题。针对AFA算法在收敛后期在极值点附近反复振荡和局部搜索能力较差的问题，本文引入单纯形法（simplex method, SM）来改进AFA算法的性能。通过数学测试算例和PSS小干扰仿真及适应性仿真实验表明，本文方法具有较好的全局搜索能力和局部搜索能力，整定的PSS参数能更好提高系统的鲁棒性。

电力系统稳定器；参数优化；SMAFA；多机系统

随着我国互联电网的发展，快速高放大倍数励磁装置越来越多地被应用于电网中，导致电网呈现弱阻尼或负阻尼状态，在外界干扰下，极易发生低频振荡[1-2]。电力系统稳定器（PSS）作为励磁系统附加阻尼控制，向电力系统提供正阻尼，能够抑制低频振荡，提高电力系统的稳定性。PSS的模型种类有很多[3-6]，有双输入信号的PSS2A[3]，多频段电力系统稳定器PSS4B[4]，广域电力系统稳定器WPSS[5]等。但是在实际电力系统的应用中，结构固定的超前-滞后型PSS因其结构简单、参数易调而被广泛地应用于电力系统阻尼控制中[6]。

PSS的参数直接影响PSS性能的优劣，若参数设定的不恰当，则不能很好地发挥PSS的性能。PSS的整定方法有相位补偿法[7-9]、极点配置法[10]以及灵敏度分析法[11]等。对于相位补偿法整定的PSS参数，只考虑一种运行工况，当系统处在其他工况时鲁棒性时达不到要求。文献[9]采用基于相位补偿的留数法来整定PSS参数，该方法简单易用，物理意义明确，但缺少协调优化不同控制器的能力；极点配置法通过选择恰当的增益矩阵，使系统达到稳定要求，但此方法存在增益矩阵难以确定的问题；近年来，有学者引入智能优化算法来整定PSS参数[12-15]。萤火虫算法是一种新兴的群体智能优化算法，由Xin-She Yang教授于2008年提出[16]。与其他智能优化算法相比，萤火虫算法概念清晰，参数设置少且设置简单，自被提出以来已经得到越来越多的应用，主要应用于光伏发电功率预测[17]、分布式电源定容和选址[18]及微网经济规划[19]等领域。目前，应用萤火虫算法来整定PSS参数的研究较少。

本文提出了SMAFA方法来对PSS进行参数整定。针对自适应萤火虫算法（AFA）存在收敛后期在极值点附近反复振荡以及局部搜索能力较弱，引入单纯形法（SM）来改进AFA。通过测试函数算例表明，SMAFA方法具有较好的全局性能及局部搜索能力。通过4机11节点算例仿真验证了本文方法整定的PSS参数能够发挥PSS的性能，并能最大限度提高了系统的鲁棒性。

1 PSS参数优化的目标函数确定

电力系统的动态模型可以用以下公式来描述：

将式（1）在平衡点取一阶近似处理，得到多机电力系统的状态方程如下所示：

式中，为系统状态矩阵；为系统输入矩阵。

PSS由放大、隔直、超前-滞后和限幅环节组成。传统超前-滞后型PSS和励磁系统如图1所示。

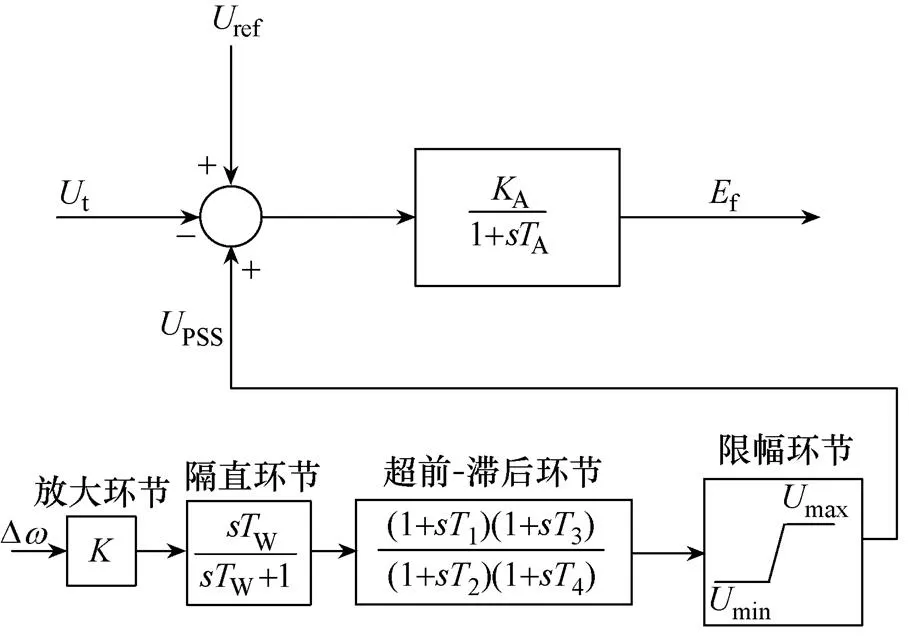
图1 带有传统超前-滞后型PSS的励磁系统

结合式（2）和图1可得，传统超前-滞后型PSS及励磁系统的传递函数为

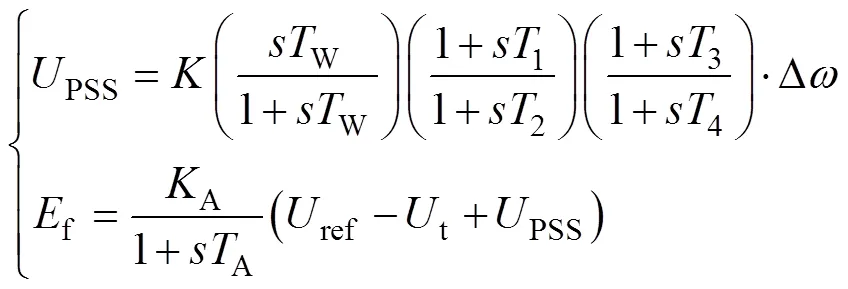
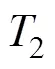
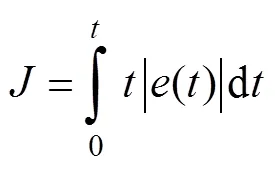
进一步地，考虑低频振荡时的有功功率振荡，式（4）可以转化为

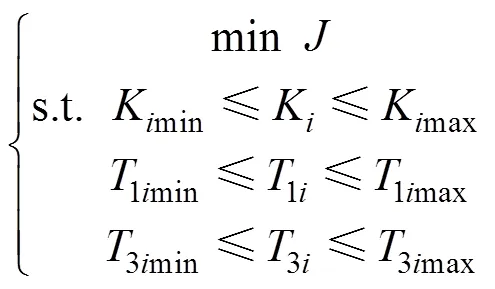
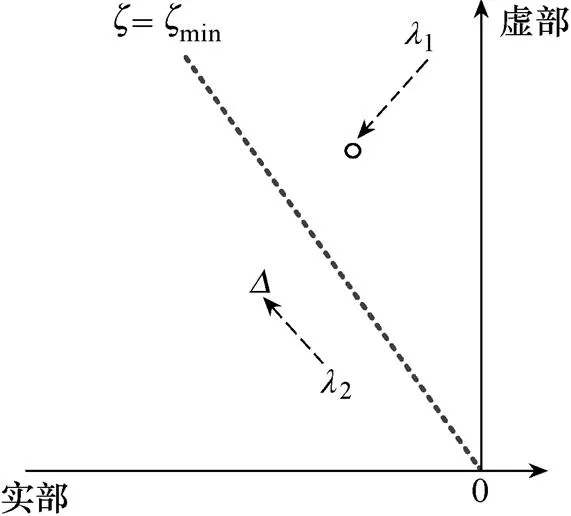
图2 特征根分布图

2 基于SMAFA的PSS优化算法

2.1 提出的SMAFA优化算法

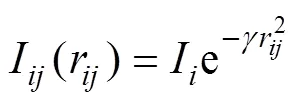
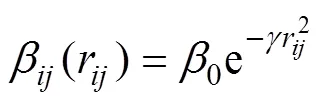
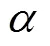
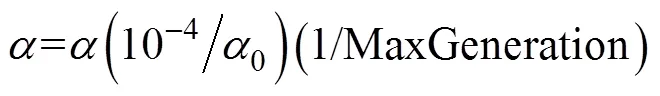
为提高萤火虫算法搜索性能，引入单纯形策略。单纯形法（SM）是由Nekler J A等人提出的应用反射、扩张、压缩等操作的较广泛使用的优化算法，是一种性能较好的局部搜索方法之一。在一次AFA算法迭代完成后，利用单纯形法搜索策略，选择K个位置较差的萤火虫进行优化，从而进一步提升PSS参数整定的效果。

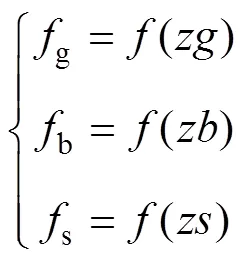
计算当前最优萤火虫位置点和次优位置点的中心位置

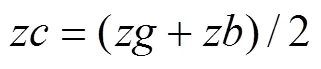
执行反射操作。计算萤火虫反射位置点

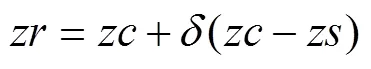
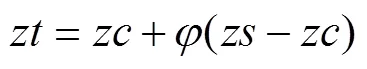
2.2 基于SMAFA算法优化PSS流程

根据2.1节，基于SMAFA算法对PSS参数优化的流程图如图3所示。

图3 PSS参数优化流程

根据图3可知，本文所提方法主要步骤如下所示：

2）萤火虫位置初始化。

3）运行仿真模型得到ITAE目标函数值。判断是否满足终止条件。若满足，则输出优化结果及最优解；若不满足，则进行步骤4）。

4）代入式（7）和式（8）得到各个萤火虫的相对亮度和吸引力大小，依照相对亮度的大小确定萤火虫的移动方向。

5）利用式（10）对萤火虫的位置进行更新并随机扰动处在最优位置的萤火虫。再次运行仿真模型，得到目标函数值。

6）根据目标函数大小（萤火虫亮度）对萤火虫按照位置最优到最差进行排序。利用单纯形法操作来更新较差萤火虫位置。

7）转步骤3），进行下一次搜索。

3 仿真分析

3.1 算法性能仿真

为了探究本文算法的收敛速度和收敛精度，构造一个二元测试函数的优化实例如下式所示：

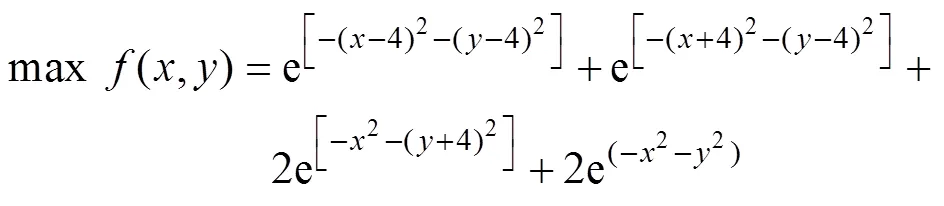
测试函数的三维曲线图如图4所示，从图中可以看出该函数在限定的范围内具有4个极值点。其中，在在函数的隶属的范围具有两个最大值，同时有两个局部的最大值为。

分别采用自适应萤火虫算法（AFA）以及单纯形的自适应萤火虫混合算法（SMAFA）在固定的迭代次数下，利用相应的最优解来表征算法的搜索精度，并与最常用的粒子群（PSO）优化算法进行比较。

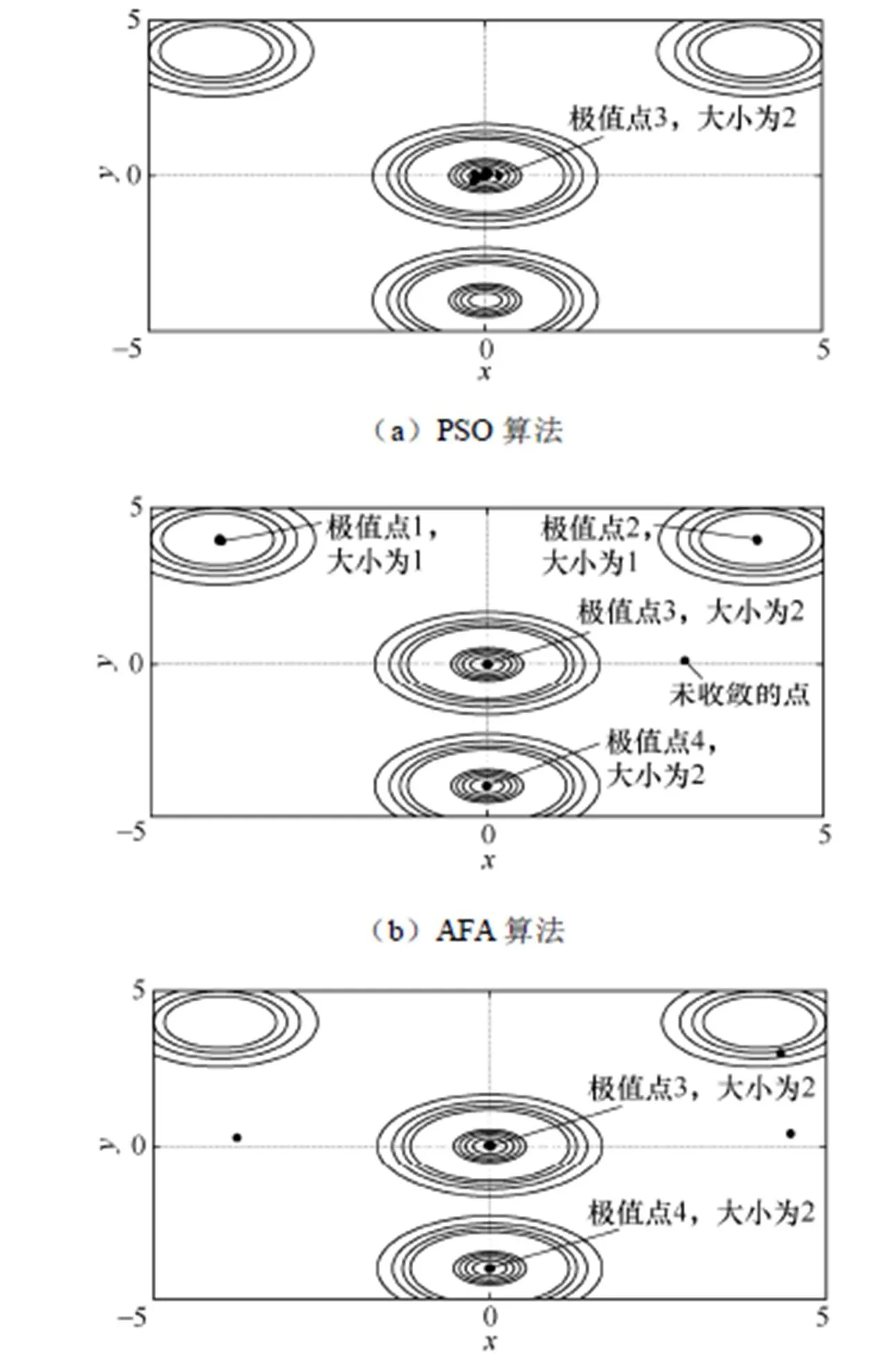
从图5（a）中可以看出，PSO算法只收敛于极值点3，陷入局部最优；图5（b）中，AFA算法具有较好的全局性，收敛于两个全局最大值极值点3和极值点4，与此同时收敛于两个局部极值，即极值点1和极值点2，由于本算例中求得是极大值，故可以看出AFA算法陷入局部最优；比较图5（a）、5（b），PSO算法容易陷入局部收敛，相比较而言，AFA算法具有较好的全局搜索性能，但其中一些萤火虫也容易陷入局部收敛；图5（c）中SMAFA算法收敛于两个全局最大值，即极值点3和极值点4，与图5（b）比较，SMAFA具有跳出局部极值的特性，说明引入单纯形改进算法性能的有效性。

由以上分析可知，PSO算法在3次迭代运算之后陷入局部最优，在28次迭代后才收敛到全局最优点；AFA算法在17次迭代后收敛到全局最优点；而SMAFA算法更快，在8次迭代次数后即收敛于全局最优点。

在相同的仿真条件下，通过50次测试3种算法总仿真平均时长，PSO、AFA、SMAFA仿真时长分别为3.8406s、4.0625s、4.3750s。表1为3种算法的最优适应度值与收敛到最优适应度值所花的时间。

表1 3种算法的结果对比

从表1中可以看出这3种算法都能收敛到最优适应度值，但是SMAFA算法的收敛时间最短，AFA算法次之，PSO算法达到收敛要求所花费的时间最长。比较仿真总时长与收敛时间还可以看出，在自适应萤火虫算法（AFA）中引入单纯形法（SM），会使得原本算法的总仿真时长变长，但是混合后的算法（SMAFA）的收敛性能大大提高，收敛所花的时间大大减小，这是混合算法的优势所在。

3.2 PSS参数优化结果

为了进一步验证SMAFA算法的性能以及PSS参数优化对系统暂态稳定的作用，本文对标准IEEE 4机两区域系统[20]进行PSS参数优化和系统性能仿真。4机两区域系统由发电机G1和发电机G2组成的区域A向发电机G3和发电机G4组成的区域B输送413MW的有功功率，该系统极易在外界干扰下发生低频振荡。考虑经济性，即不可能在所有发电机上都安装PSS，采用留数法采实现PSS的最佳配置，即在提高系统鲁棒性的同时，使PSS的安装数量最少。各发电机的模态留数模值的结果见表2。

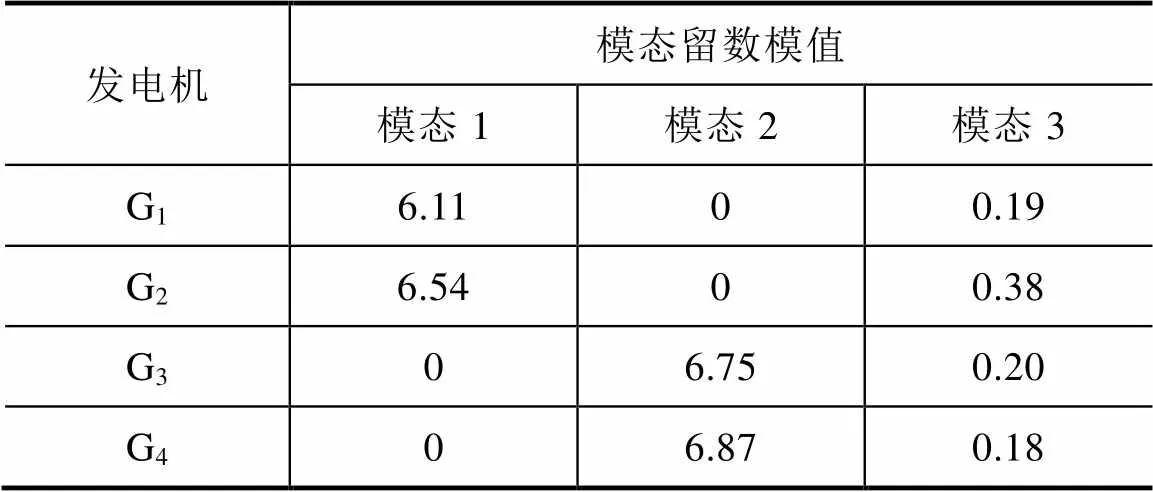
表2 各发电机的模态留数模值

从表2中的数据可以看出，对于区域1中的模态1在留数上只体现与发电机G1、G2有关；模态2同样只与发电机G3、G4有关；而模态3与发电机G1、G2、G3、G4都有关。对比留数的模值可以知：对于模态1在发电机G2配置PSS效果最好；而模态2在发电机G4配置PSS效果较好；同样，模态3在发电机G2配置PSS效果较好。综上，为了能够更好的抑制低频振荡，提高系统的鲁棒性，本文将考虑在发电机G2、G4上面配置PSS。

对4机两区域系统在1s时刻对发电机G2和发电机G4施加持续时间为0.1s，幅值为0.05的脉冲干扰信号。分别采用AFA算法和SMAFA算法进行PSS参数的优化，两种算法优化的目标函数适应度收敛曲线如图6所示。从图中可以看出，SMAFA算法的收敛精度优于比AFA算法。

图6 算法优化PSS参数结果目标函数适应度值

两种算法的PSS参数优化结果见表3。

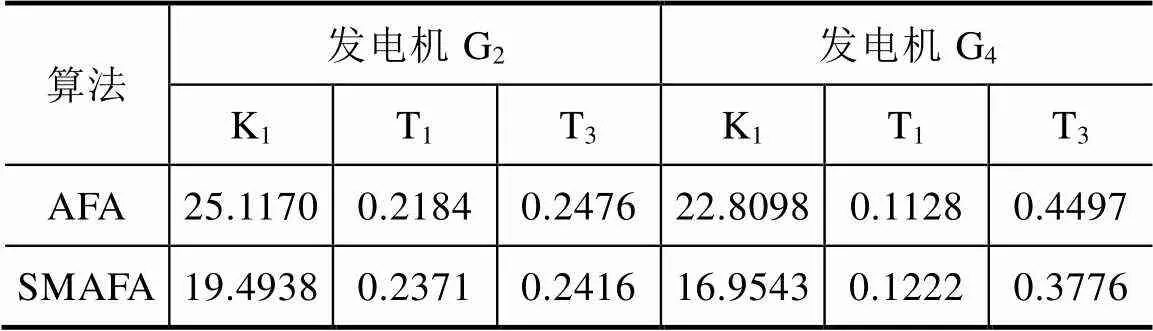
表3 算法优化PSS参数结果

3.3 动态仿真结果分析

1）小扰动情况下PSS有效性分析

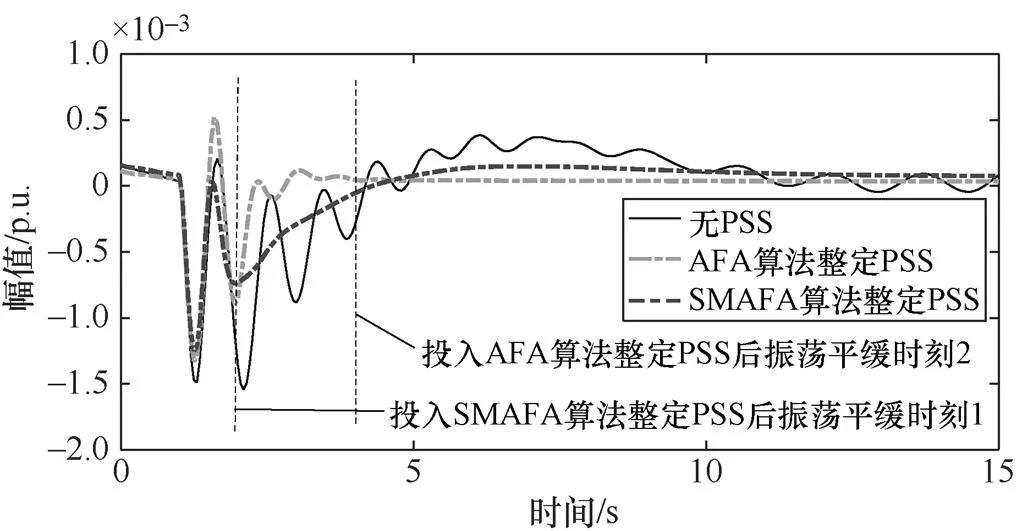
为了评价基于SMAFA算法优化的PSS性能，对4机两区域系统在1s时刻对发电机G2和发电机G4施加持续时间为0.1s，幅值为0.05的脉冲干扰信号。对配置了采用AFA、SMAFA算法优化的PSS系统进行小扰动动态仿真。发电机G2和发电机G4的转速变化曲线如图7所示。

（a）发电机G2

（b）发电机G4

图7 发电机角速度变化曲线（小扰动）

由图7可以看出，在未安装PSS的情况下，发电机角速度的振荡无法衰减到平衡；在加装PSS后系统的振荡得到了很好的抑制。AFA算法整定的PSS与SMAFA算法整定的PSS相比，后者振荡曲线平缓的时刻较短，后者的曲线较为平缓，具有更好的抑制低频振荡的效果。

表4给出了采用PSS前后发电机G1—G4转速曲线和联络线功率曲线的最小阻尼比变化。

表4 安装PSS前后阻尼比变化

从表4中可以看出，系统在没有安装PSS时，在扰动干扰下，各发电机及联络线的最小阻尼比都为负阻尼，威胁着系统的稳定运行。在加装AFA算法和SMAFA算法整定的PSS后，各发电机的阻尼都有大幅的提高，低频振荡得到抑制，系统的鲁棒性增强，相比而言，SMAFA算法整定的PSS能更大提高发电机角速度与联络线功率的阻尼比。所以，本文方法整定的PSS在系统小扰动情况下使系统具有更高的鲁棒性能。

2）大扰动情况下PSS有效性分析

为验证SMAFA整定PSS参数的暂态性能，对4机两区域系统进行如下大干扰：在1s时刻使联络线发生三相短路，其持续时间为1/6s。采用传统相位补偿法对PSS进行参数整定，并与3.2节SMAFA整定的参数进行对比，结果见表5。

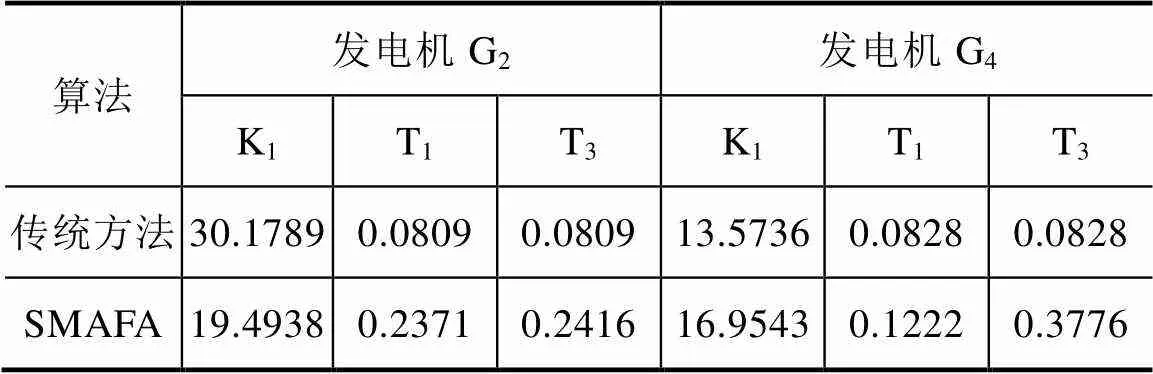
表5 用于大干扰仿真的参数

采用表5所示参数整定PSS，并将整定的PSS投入系统中运行，与未加装PSS的振荡结果进行对比，结果如图8所示。图8为发电机G4转速变化曲线及联络线功率变化曲线。

（a）发电机G4角速度

（b）联络线功率

图8 电气量变化曲线

从表6中的信息可以看出，未加PSS的系统为负阻尼状态，最小阻尼比为-0.0333；投入PSS后的系统的阻尼比提高，为正阻尼，其中最小阻尼比为0.0781，满足要求系统阻尼比至少为0.05的要求，系统稳定性增强，鲁棒性提高。

表6 阻尼比及特征根

4 结论

为了抑制电力系统低频振荡，本文讨论了对多机电力系统稳定器优化的问题，提出一种基于单纯形策略的自适应萤火虫算法来对传统超前-滞后型PSS进行参数整定。通过数值仿真，验证了本文方法具有较好的全局搜索能力和局部搜索能力，在满足收敛精度的要求下，与传统方法相比收敛速度快；将本文方法应用于4机两区域的PSS参数优化整定，小干扰仿真结果表明本文方法整定的PSS参数能够有效提高系统的阻尼比和鲁棒性；同时，实验仿真也表明整定后的PSS能够有效地抑制系统低频振荡。

[1] 金涛, 刘对. 基于广义形态滤波与改进矩阵束的电力系统低频振荡模态辨识[J]. 电工技术学报, 2017, 32(6): 3-13.

[2] 陈剑, 周宇植. 基于PMU的分布式次同步振荡在线辨识方法[J]. 电气技术, 2017, 18(10): 92-95.

[3] 张俊峰, 李鹏, 郭琦. PSS2A模型的负阻尼案例分析及检测方法[J]. 电力系统自动化, 2014, 38(2): 127-130.

[4] 赵晓伟, 谢欢, 吕思昕, 等. 电力系统稳定器PSS4B的参数整定及现场试验[J]. 电网技术, 2016, 40(2): 508-513.

[5] 陈刚, 程林, 张放, 等. WPSS输入反馈时延的自适应分段补偿设计[J]. 电力系统自动化, 2013, 37(14): 25-31.

[6] 边晓燕, 施磊, 宗秀红, 等. 多运行方式下风电机组变频器参与次同步相互作用的分析与抑制[J]. 电工技术学报, 2017, 32(11): 38-47.

[7] 杜文娟, 王海风, 曹军. PSS就地相位补偿法的模型和理论[J]. 中国电机工程学报, 2012, 32(19): 36-41.

[8] Larsen E V, Swann D A. Applying power system stabilizers[J]. IEEE Transactions on Power Apparatus and Systems, 1981, 100(6): 3017-3046.

[9] Zhang Junbo, Chung C Y, Han Yingduo. A novel modal decomposition control and its application to PSS design for damping interarea oscillations in power systems[J]. IEEE Transactions on Power Systems, 2012, 27(4): 2015-2025.

[10] 袁野, 孙元章, 程林. 基于多信号在线辨识的广域PSS协调设计[J]. 电力系统自动化, 2010, 34(8): 14-19.

[11] 史慧杰, 陈陈, 陈迅, 等. 基于灵敏度分析的电力系统稳定器参数优化[J]. 电力系统自动化, 2012, 36(17): 15-19.

[12] 宗鹏鹏, 王培秀, 闫济红, 等. 计及随机性的电网低频振荡实时修正控制研究[J]. 电气技术, 2017, 18(2): 25- 30.

[13] 胡晓波, 杨利民, 陈中, 等. 基于人工鱼群算法的PSS参数优化[J]. 电力自动化设备, 2009, 29(2): 47-50.

[14] 郭成, 李群湛, 王德林. 基于Prony和改进PSO算法的多机PSS参数优化[J]. 电力自动化设备, 2009, 29(3): 16-21.

[15] Wang Z, Chung C Y, Wong K P, et al. Robust power system stabiliser design under multi-operating conditions using differential evolution[J]. IET Generation Transmission & Distribution, 2008, 2(5): 690-700.

[16] 王昕, 黄柯, 郑益慧, 等. 基于萤火虫算法-广义回归神经网络的光伏发电功率组合预测[J]. 电网技术, 2017, 41(2): 455-461.

[17] Yang X S. Nature-inspired metaheutistic algo- rithms[M]. Luniver Press, 2008.

[18] 陈家俊, 蒋铁铮, 周勇, 等. 考虑电压骤降的分布式电源定容和选址[J]. 电网技术, 2014, 38(8): 2244- 2249.

[19] 王晶, 王宗礼, 陈骏宇, 等. 基于萤火虫优化算法的微网源-荷博弈模型及分析[J]. 电力系统自动化, 2014, 38(21): 7-12.

[20] Farmer R G. Second benchmark model for computer simulation of subsynchronous resonance IEEE subsynchronous resonance working group of the dynamic system performance subcommittee power system engineering committee[J]. IEEE Power Engineering Review, 1985, 5(5): 34-34.

The multimachine power system stabilizer parameters optimal design based on SMAFA optimization algorithm

Zhan Renjun

(Fujian Shuikou Power Generation Group Co., Ltd, Fuzhou 350000)

The performance of traditional power system stabilizer is greatly influenced by its own parameters. In order to maximize the performance of the power system stability, the current research mainly uses optimization algorithms for the tuning of PSS parameters. As an emerging swarm intelligence optimization algorithm, adaptive firefly algorithm (AFA) is very suitable for power system op-timization problems because of its good global search capability. In view of its problems of poor local search ability and easily oscillating at extreme point, combining the adaptive firefly algorithm with the simplex method, this paper proposes a new SMAFA method to improve the PSS optimization performance. Through the mathematics test and PSS interference and adaptive simulations, the proposed method is proved to have good global search ability and local search ability, and it can be better to improve the robustness of the power system.

power system stabilizer; parameters optimization; SMAFA; multi-machine system

2018-05-23

詹仁俊（1963-），男，高级工程师，主要研究方向：电网调度运行及其自动化。