超几何分布与二项分布的错解和正解的数学期望值相等

武增明

(云南省玉溪第一中学 653100)

一、问题的由来

在我校2017届数学模拟考试中有两道涉及超几何分布与二项分布的概率题目，学生做得很不理想.具体题目如下：

1.为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图(如图1)，已知图中从左到右的前3个小组的频率之比为1∶2∶3，其中第2小组的频数为4.

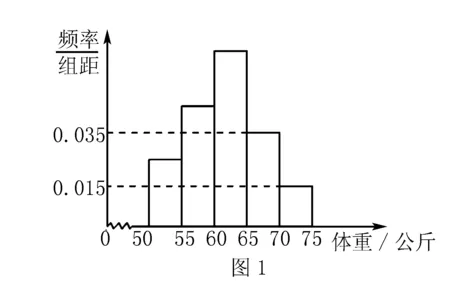
(1)求该校报考飞行员的总人数；

(2)以这所学校的样本数据来估计全省的总体数据，若从全省报考飞行员的同学中(人数很多)任选3人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望.

2.某中学动员学生在2017年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生，他们参加活动的次数统计如图2所示.

(1)求合唱团学生参加活动的人均次数；

(2)从合唱团中任选2名学生，求他们参加活动次数恰好相等的概率；

(3)从合唱团中任选2名学生，用ξ表示这两人参加活动次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ.

不少学生在解答这两题的最后一问时出现了如下的典型错误：

1.(2)错解 由题知，体重在60公斤以下的有6人，60公斤以上的有10人.随机变量X服从超几何分布且可以取：0，1，2，3.

2.(3)错解 由题知，在每次抽取中，抽到参加1次、2次、3次活动的概率分别为0.1，0.5，0.4；

随机变量ξ的取值为0，1，2.

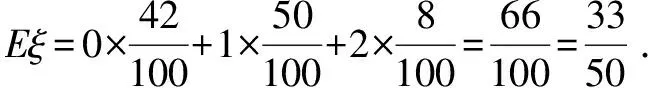
为了便于说明问题，我们给出两题的正确解答.

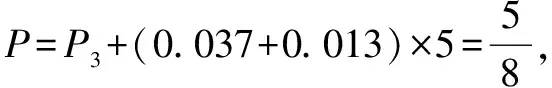
所以X服从二项分布，

随机变量X的分布列为：

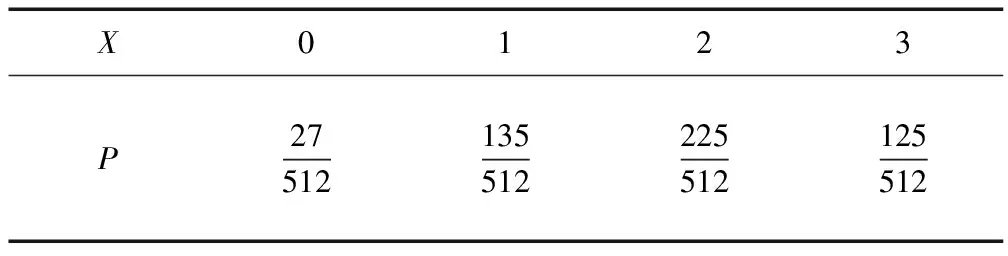
X0123P27512135512225512125512

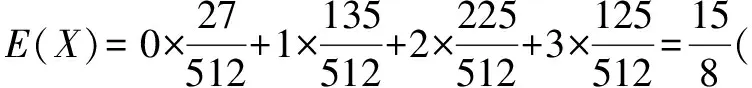
2.3正解 随机变量ξ的取值为0，1，2，

ξ的分布列为：

ξ012P41995099899

数学期望

反思上述两题中学生所犯的典型错误，我觉得我们需要思考为什么正解与错解中的数学期望值相等这个问题.

二、问题的解决

超几何分布定义(普通高中课程标准实验教科书，数学2-3(A)，2009年4月第3版)：

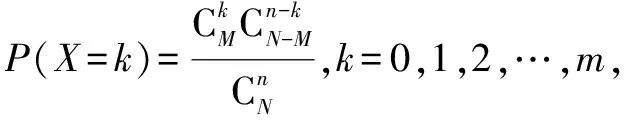
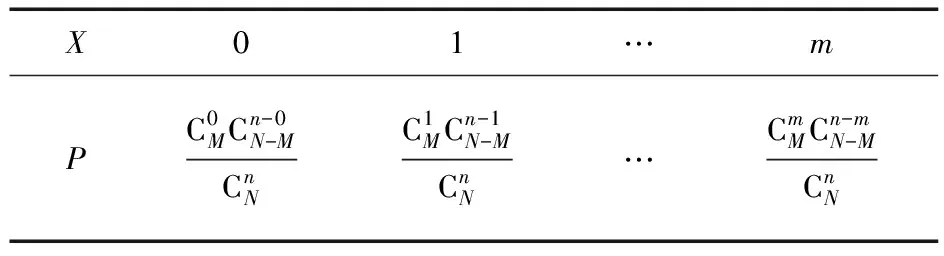
X01…mPC0MCn-0N-MCnNC1MCn-1N-MCnN…CmMCn-mN-MCnN

为超几何分布列，称随机变量X服从超几何分布.

依数学期望的定义公式有：

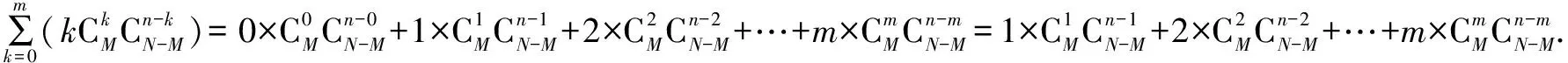
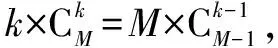
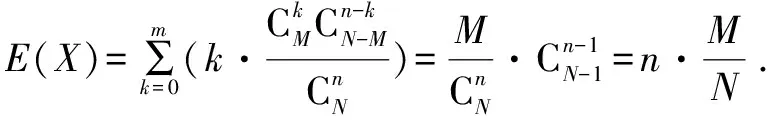
故超几何分布与二项分布的错解和正解的数学期望值相等.