2219铝合金搅拌摩擦焊缝装配质量的响应曲面法建模及分析
石 璟 余卓秋 黄小鲁 黄举近 李 辉
(1 四川航天长征装备制造有限公司,成都 610100)
(2 电子科技大学,成都 611731)
0 引言
搅拌摩擦焊接技术作为一项绿色高效的固相连接技术,能够实现铝合金、钛合金、镁合金、铜合金及钢等同种材料及异种材料之间的连接。经过20多年的发展,该技术已在航空航天、舰船装备、轨道交通、新型汽车、电力电子等领域的相关结构件制造方面得到了广泛的应用[1-3]。
搅拌摩擦焊有着广泛的应用领域,其焊接性能受焊缝装配质量的影响。对搅拌摩擦焊接技术而言,焊缝间隙、焊缝错缝以及搅拌针与焊缝中心的对中情况(后文简称焊缝对中)等是组成对焊工艺焊缝装配质量的要素,如图1所示。但是在实际焊接过程中,由于受到焊接设备、工装夹具、结构加工精度、薄壁件曲翘变形等因素的影响,焊缝的装配质量总会存在一定的偏差,而装配偏差往往会导致焊缝接头性能的下降[4-6]。近年来,相关学者针对搅拌摩擦焊接焊缝装配质量问题进行了相关研究,但是,现有的研究方法依然存在一些不足。例如,文献[5-6]分别研究了焊缝间隙、焊缝错变量以及焊缝对中等装配要素对接头强度的影响,并针对单个装配要素给出了容差上限值。需要注意的是,在实际的焊接过程中,焊缝间隙、错缝及焊缝对中等问题同时出现,焊缝接头质量是上述要素的综合作用结果。然而,如何描述各装配要素对焊缝接头性能产生的综合影响,尚未发现有效的解决办法。
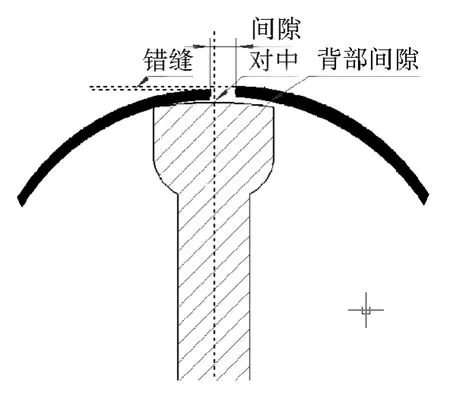
图1 搅拌摩擦焊焊缝装配质量要素Fig.1 Elements of assembly quality of friction stir welding
结合上述分析,本文提出了一种利用响应曲面法,反映焊缝装配质量与焊缝接头性能之间联系的方法。
1 模型建立
1.1 响应曲面法
响应曲面法(RMS)是一种全局近似模型的方法。它以数学建模和统计学原理为基础,利用统计学的综合试验技术解决复杂系统输入和输出之间关系,可对受多个自变量影响的响应进行建模与分析。对于焊缝装配质量与接头性能这类具有高度非线性响应的问题,响应面法可以将响应函数与多个自变量之间的复杂关系表示为简单的显式函数[7],为后续的分析工作提供良好基础。
一般而言,响应面函数的选取应满足两方面的基本要求[8]:
(1)在能够反映真实响应关系特征的前提下,响应函数应尽可能地简化;
(2)选取响应面函数时应尽可能减少待定系数的数量,以方便快速计算。
研究经验表明,采用二次多项式就能满足大多数系统的要求,其表达式为:
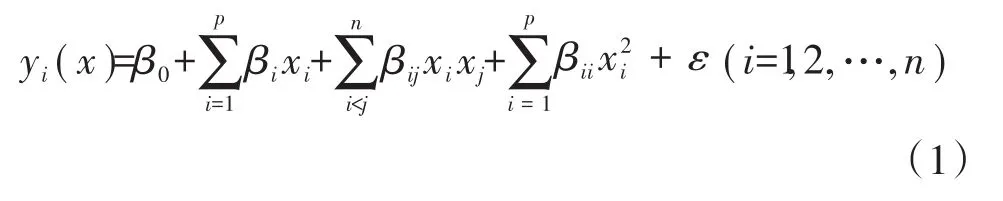
式中,yi(x)是响应函数,x1,x2,…,xn是多个自变量,ε代表随机误差,βij为xh和xi之间的交互效应;βii为xi的二次效应[9]。
在得到公式(1)所描述的响应表面后,可以通过方差分析中的参数R2对响应面模型的拟合程度进行验证,其值越接近1,说明模型的拟合精度越高。R2的定义为:

式中,n是设计点的个数分别是相应自变量的实测值、预测试和平均值。
1.2 设计方案选择
常见的响应曲面法的设计模型主要有CCD(Central Composite Design)和 BBD(Box-Behnken Design)两种,其中CCD方法又可细分为外切中心复合设计(CCC)、内切中心复合设计(CCI)、面心立方设计(CCF)等[10]。不同的设计模型响应有不同的试验点,4种经典的二阶响应曲面设计方案各有优劣。在试验操作方面,CCF和BBD更为简单,从预测的性能方面,因CCF不具有旋转性,所以在保持精度一致性方面相对较差。模拟参数估计方面,CCC较优,而BBD最差[11]。鉴于上述分析,选择CCC法进行实验设计。
CCC设计的试验点主要由下面3个部分组成:
(1)mc个角点,如图2中立方体的顶点(蓝色)所示,其为各个因子的边界值,组成了该设计的因析部分;
(2)2k个星点,如图2中垂直于立方体面的轴线端点(绿色)所示,k为试验中的因子的个数;
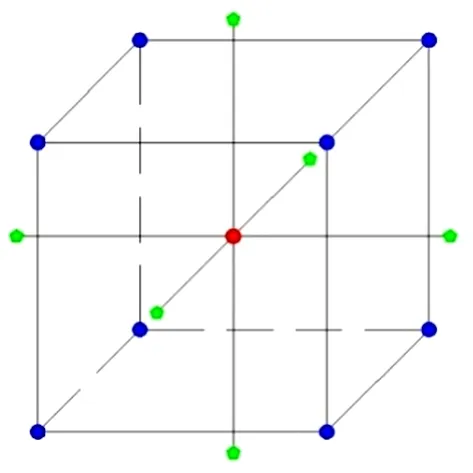
图2 响应曲面法主要试验点Fig.2 Main test points of response surface methodology
(3)m0个角点,在试验区域的中心进行m0次重复试验。
在此实验中,mc=8,k=3,m0=6,则总体实验数目:
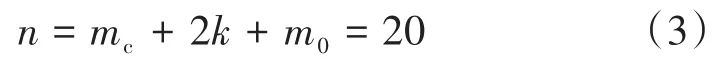
1.3 响应曲面试验设计
试验使用材料为2219-T87铝合金轧制板,其大小尺寸为300 mm×150 mm×6 mm,相关材料的力学性能分别取:破坏强度(σb)为440 MPa,材料延伸率为15%。主要化学成分如表1所示。

表1 2219铝合金化学成分Tab.1 Chemical composition of 2219 aluminum alloy%(质量分数)
使用自行研制的搅拌针,分为预焊搅拌针与正式焊搅拌针两种,其中正式焊搅拌针带有右旋螺纹。两种搅拌针的结构参数如表2所示。
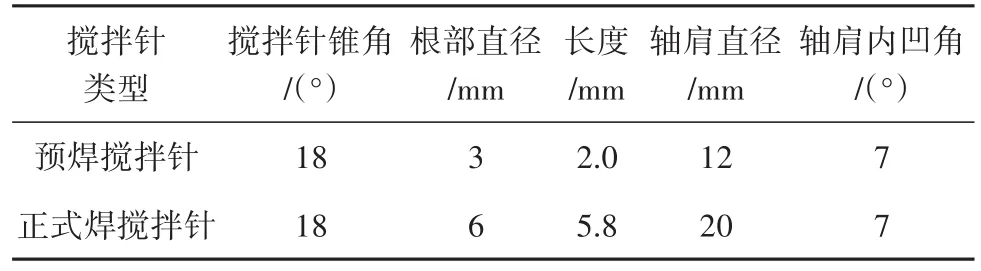
表2 实验用搅拌针结构参数Tab.2 Geometry parameters of FSW tools for experiments
通过前期的一系列基础实验积累,获得理想装配条件下焊接工艺优化参数为:预焊时,搅拌针转速800 r/min、进给速度为400 mm/min;正式焊时,搅拌针转速600 r/min,进给速度为200 mm/min、轴肩下压量0.2 mm。选取焊缝间隙、焊缝错缝和焊缝对中作为响应曲面法的考察因素,并以1、0、-1分别代表其高、中、低水平。由于在实际焊接过程中,通过长期的工艺积累发现,焊缝间隙在0.5 mm以下时,采用“预焊+正式焊”工艺,一般都能满足焊缝接针的强度及延伸率要求,但是随着焊缝间隙值的进一步扩大后,预计其强度会出现较大的降低。另一方面,在实际焊接过程中,特别是针对曲线焊缝进行焊接时,由于薄壁曲面焊缝的变形,使得焊缝间隙最大可达2 mm。因此,重点关注焊缝间隙在0.5~2 mm情况下装配质量对焊缝接头性能的影响。结合实际生产情况,各因素的取值范围分别为:焊缝间隙值为0.5~2.0 mm,焊缝对中偏差值为-0.6~0.6 mm,焊缝错缝量为-0.3~0.3 mm。以焊缝前进侧所在的一边作为标志,对装配质量要素中的“焊缝对中”一项,当搅拌针偏置向前进侧的一边,记为正值,当搅拌针偏置向后退侧的一边,记为负值;同理,对装配质量要素中的“焊缝错缝”一项,当前进侧母材高于后退侧,记为正值,反之则记为负值。编码后的因素水平见表3。
按照标准GB/T 2649—1989和GB/T 228.1—2010,沿垂直于焊接方向将焊接接头切成标准试样,每组三个,在CMT5305型拉伸试验机上进行拉伸试验,加载速率为3 mm/min,并记录接头的破坏强度与延伸率,完成后取三个试样的平均值作为采样值。
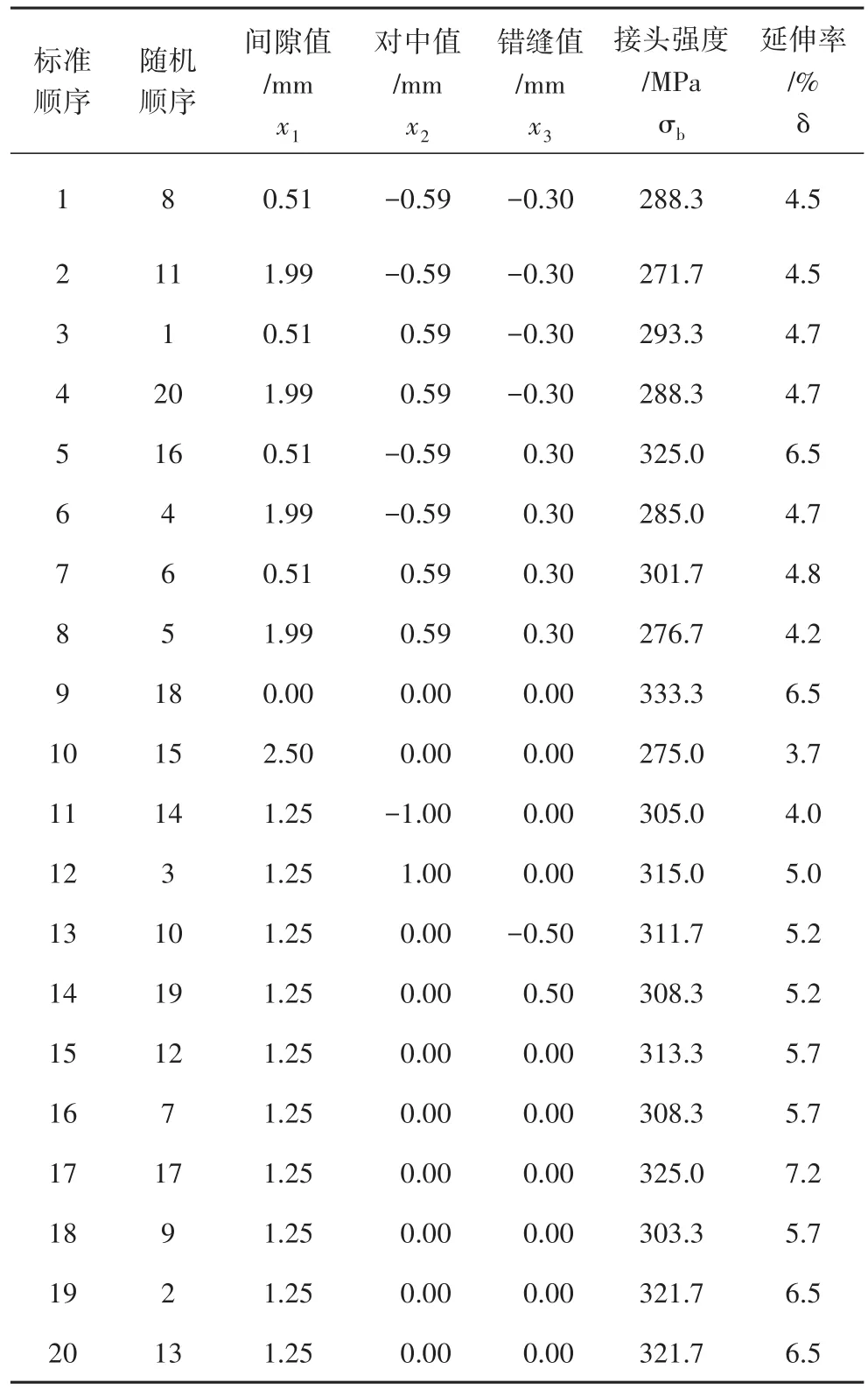
表3 中心组合设计参数Tab.3 Parameters of central composite design
2 焊缝装配质量响应曲面建模及分析
2.1 响应曲面模型的建立
对表3中的数据进行多元回归拟合,分别得到焊缝间隙值x1,焊缝对中值x2,焊缝错缝值x3与接头强度σb与延伸率δ之间的回归模型分别为

由ΔF检验(F检验又称方差齐性检验的值),当P(概率)>ΔF的值<0.05时,即可认为该指标显著。由表4可以看出,焊缝接头强度、延伸率等的显著性指标明显,测量值R2>0.74,说明回归方程能够较好地模拟真实的曲面,拟合检验也表明回归方程不失拟。
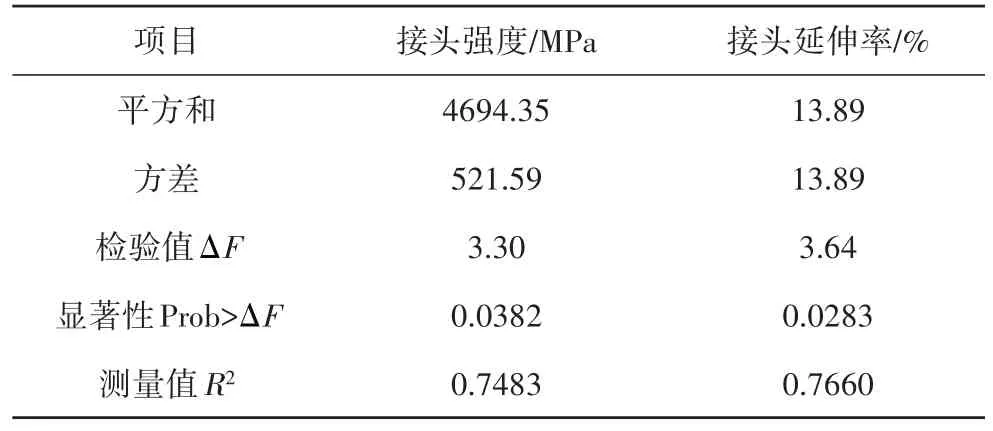
表4 模型方差分析Tab.4 Variance analysis of model
2.2 单一装配质量要素对焊缝接头性能的影响
根据响应曲面模型,图3描述了各项装配条件均在中心点时(即装配间隙为1.25 mm,焊缝对中和错缝量均为0的情况),模型所预测的各装配要素对焊接接头强度及延伸率的影响。由图3(a)可知,随着焊缝间隙的不断增大,接头强度出现明显的下降,并且强度下降的速率越来越大,且接头延伸率的变化情况也具有相同的趋势。例如当焊缝间隙为0.51 mm时,焊缝接头强度可达322.21 MPa,接头延伸率约为6.33%;随着焊缝间隙的不断增大至2.0 mm时,其接头强度降至294.87 MPa,接头延伸率仅有5.26%左右。而搅拌针的非对中量和板材的错缝高差对接头的强度很有限,例如在搅拌针对中偏差为0和0.6 mm时的强度差值只有5 MPa,但接头延伸率却由6.21%降为5.58%。从上述分析可以看出,装配间隙对接头性能的影响最为明显。
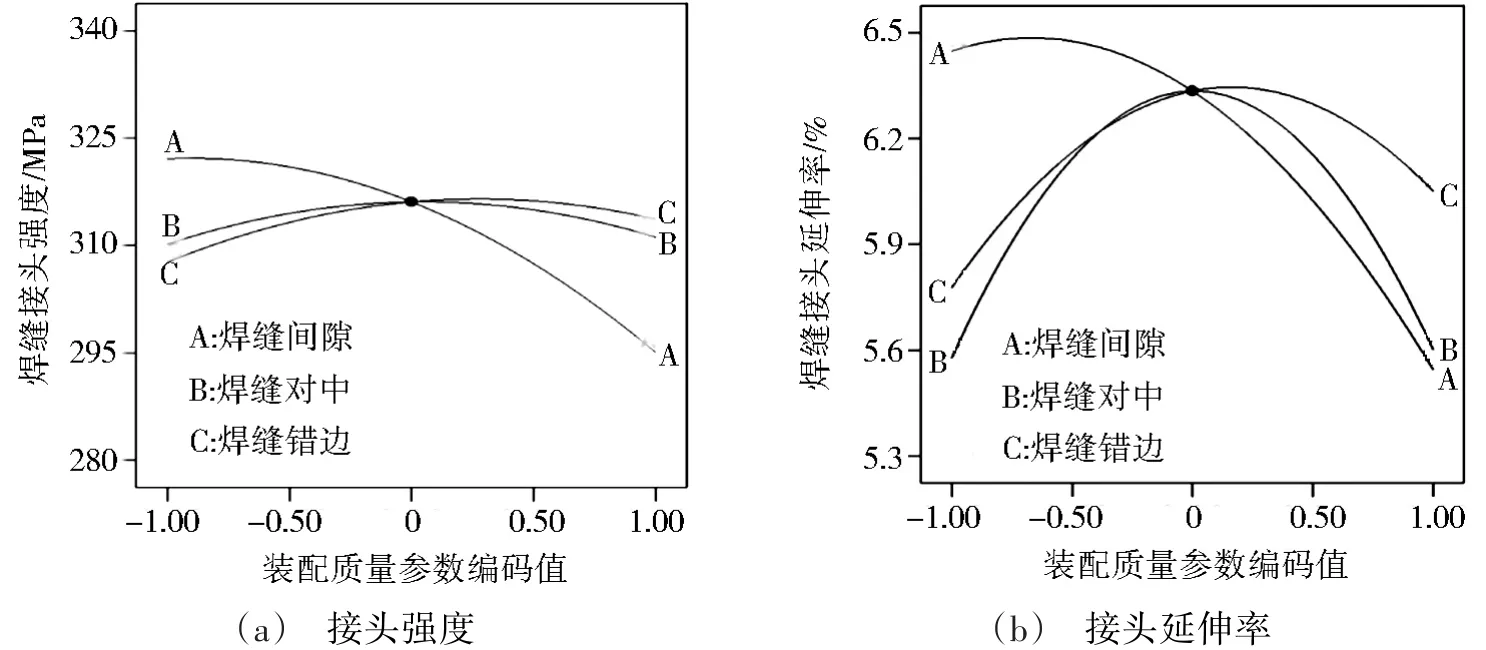
图3 单一装配质量要素对焊缝接头强度和延伸率的影响Fig.3 Effect of single assembly quality elements on UTS and elongation of weld joint
2.3 装配质量要素的交互作用对焊缝接头性能的影响
2.3.1 装配间隙和焊缝对中对接头性能的影响
由图4(a)和(b)可以看出,随着焊缝间隙的不断增大,接头的强度和延伸率均呈现下降的趋势,并且趋势愈发的明显。但是焊缝对中情况对接头的强度影响不明显,此趋势与文献[6]中所描述的情况一致。同样,焊缝对中情况对于接头延伸率的影响也不是十分明显。从图4(c)和(d)可以看出,焊缝对中情况对接头强度的影响呈现出非对称性,当搅拌针发生偏置后,焊缝后退侧的接头强度会略高于焊缝前进侧,但是这一效应随着焊缝间隙的增大而不断弱化。这种影响对于焊缝接头强度同样适用,但是其所表现出的非对称性并不明显。
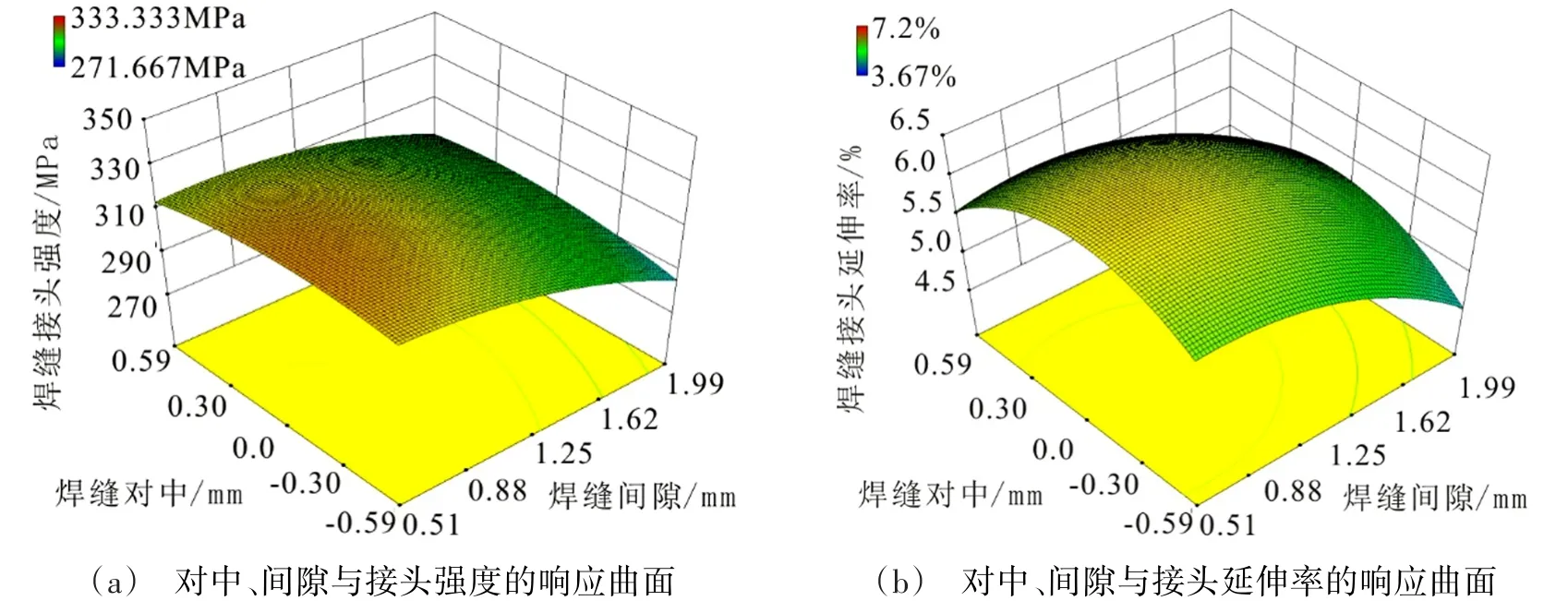
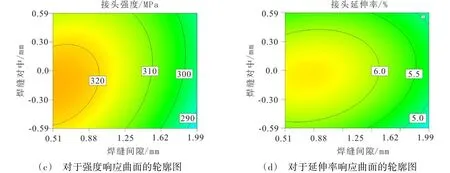
图4 装配间隙和焊缝对中对接头性能的影响Fig.4 Effect of gap and NCOP on joint performance
2.3.2 装配间隙和焊缝错缝对接头性能的影响
在装配间隙和焊缝错缝因素对接头性能的影响中,装配间隙依然占主导地位。由图5(a)和(b)可以看出,随着焊缝间隙的不断增大,接头的强度和延伸率依旧呈现下降的趋势。而焊缝错缝对接头强度的影响因素在幅度上并不明显,但是却表现出来明显的非对称性,如图5(c)和(d)所示。当前进侧错缝量高于后退侧时,焊缝的强度会出现一定的上升,但是该非对称性随着焊缝间隙的增大而逐渐弱化,相同的特点对焊缝接头的延伸率也是适用的。
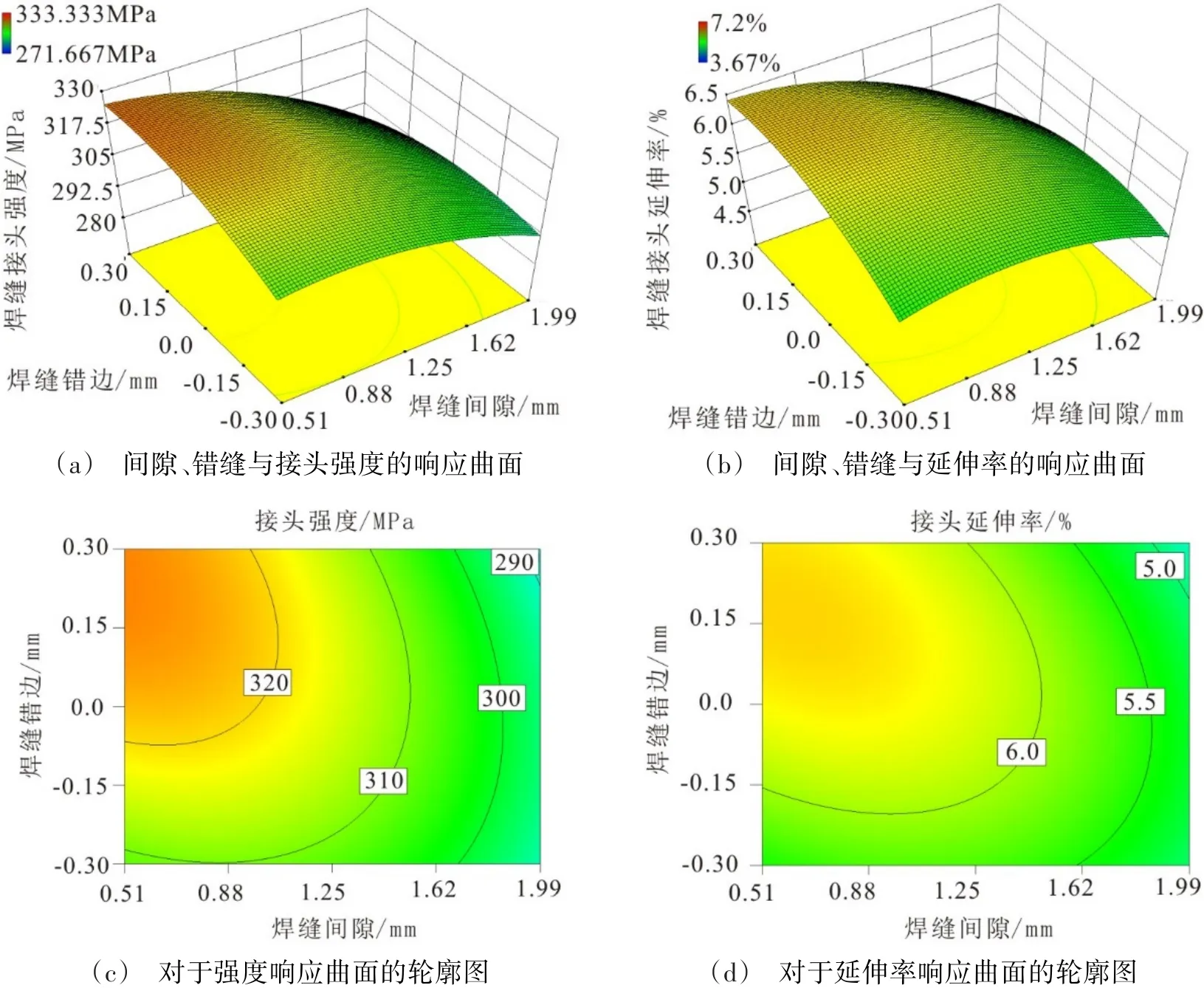
图5 装配间隙和焊缝错缝对接头性能的影响Fig.5 Effect of gap and misalignment on joint performance
2.3.3 焊缝错缝和焊缝对中对接头性能的影响
与焊缝间隙对接头性能产生的影响相比较,焊缝错缝和焊缝对中等装配要素的影响并不明显,但是这种影响却表现出明显的非对称性。如图6(a)和(c)所示,焊缝错缝和焊缝对中在变化范围内对接头强度的影响在20 MPa以内。当搅拌针偏向前进侧,而前进侧的错缝量低于后退侧时;或者,当搅拌针偏向后退侧,而前进侧的错缝量高于后退侧时,焊缝接头的强度会略有上升,但是在相反的情况下,接头强度略有下降。相同的趋势在接头的延生率指标中也有类似的表现,如图6(b)和(d)所示。
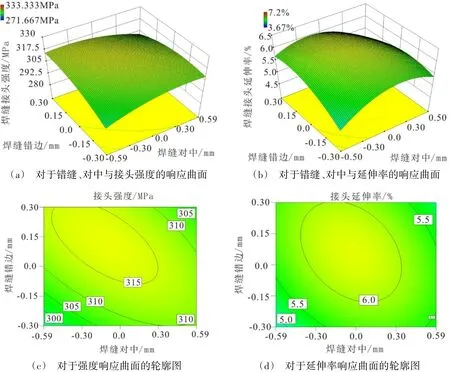
图6 焊缝错缝和焊缝对中对接头性能的影响Fig.6 Effect of misalignment and NCOP on joint performance
3 装配质量分析对实际工作的指导意义
利用响应曲面法,在获得各装配要素对最终接头强度和延伸率的影响趋势的同时,还可以利用其拟合得到的回归方程来指导实际工作。其实现思路为:依据最终接头的性能要求,来获取装配要素的上下限边界值,从而为制定合理的装配工艺参数提供理论与量化的判定条件,减少因依赖人工经验判断的而造成的不确定性。
将装配质量的每一个要素所代表的值视为一个坐标轴,则三个要素构成了一个三维空间,空间中的各个点对应着一种具体装配情况。但是并非所有的装配情况都能满足接头性能的焊接性能需求,因此,需要在上述三维空间中搜索可行装配条件所在的区域,称之为满足接头性能需求的装配质量可行空间。通过一个实例来描述可行空间的搜索过程。
以6 mm厚的2219-T6铝合金板材焊接为例,焊接工艺参数采用本文2.3节中描述的各项参数。同样,设x1,x2,x3分别为代表缝装配质量要素中的焊缝间隙、焊缝对中与焊缝错缝量,在满足焊接接头强度σb≥300 MPa、接头延伸率δ≥3%的情况下,求解焊缝装配质量参数的约束边界,得到各类装配条件的集合即为焊缝装配质量参数的可行空间。结合实际加工特点,可初步设定装配质量可行空间的搜索范围满足:
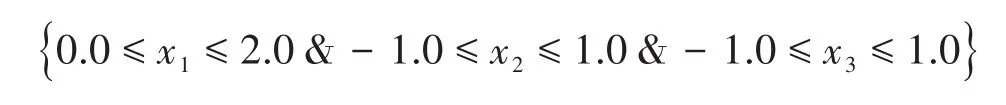
对可行空间的搜索问题,实际可转换为非线性规划问题,由于本文重点关注焊缝装配质量的工艺问题,因此对非线性规划问题的求解过程不展开讨论,相关方法请参考文献[12]。通过搜索,可得到装配质量参数可行空间的形貌如图7所示。可获得可行空间在各个维度上的极值,得到可行空间在各个维度上的极值为:
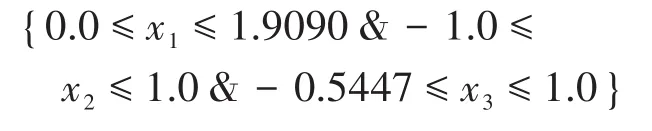
如果将接头质量的条件调整为接头强度σb≥330 MPa,接头延伸率δ≥4%时,则可以发现装配质量参数可行空间会明显的缩小,如图8所示。
同理,可获得可行空间在各个维度上的极值为:
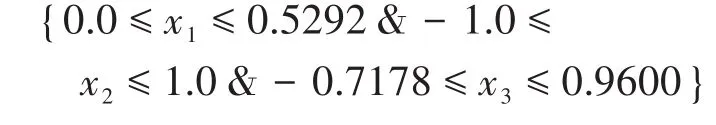
依据上述方法,可以得到满足各种焊接性能要求的装配质量参数可行空间。针对具体的焊缝装配情况,当判定对应装配质量各要素的组合值在可行空间范围之内,则可以认为该装配条件能够满足接头的焊接性能要求,从而为判断焊缝装配质量是否合格提供了量化依据。
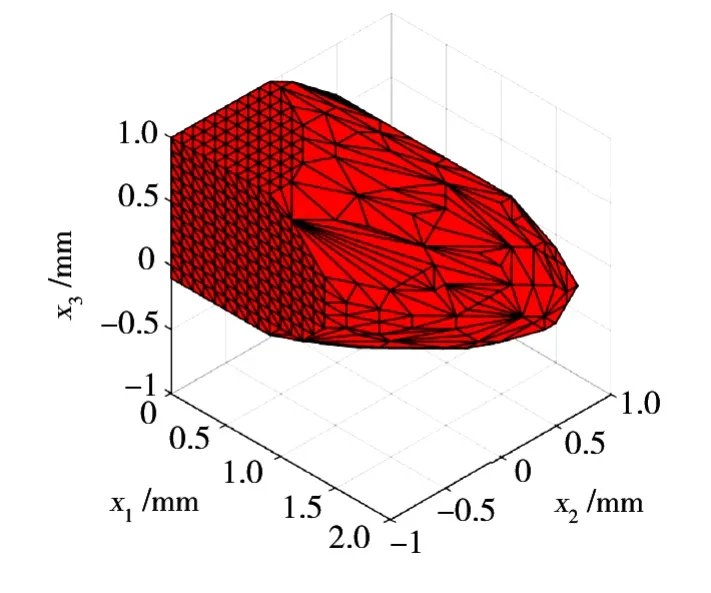
图7 σb≥300 MPa,δ≥3%的装配质量参数可行空间Fig.7 Assembly quality parameter space under the condition of σb≥300 MPa,δ≥3%
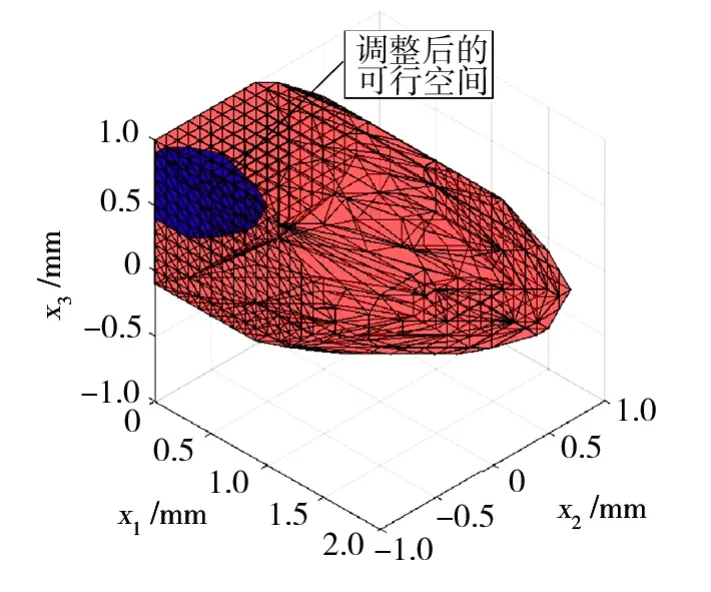
图8 σb≥330 MPa,δ≥4%的装配质量参数可行空间Fig.8 Assembly quality parameter space under the condition of σb≥330 MPa,δ≥4%
4 结论
(1)基于响应面法,建立了搅拌摩擦焊装配质量要素(包括焊缝间隙、焊缝对中和焊缝错缝)对2219-T6铝合金焊缝接头性能之间的数学模型,为焊缝装配质量与焊缝接头性能之间的联系提供了直观的描述。
(2)焊缝间隙在装配质量要素中是影响包括接头强度和延伸率在内的接头性能的关键因素,随着装配间隙的不断增大,接头性能参数会出现明显的下降。另一方面,在焊缝错缝和焊缝对中等因素的影响下,焊缝的接头性能的下降程度关于焊缝中线表现出非对称性。
(3)针对实际生产需求,利用响应曲面建模方法,依据焊缝的接头性能要求,可以通过搜索得到对应的装配质量可行空间,为制定合理的工艺参数和检测标准提供便利。

