驾驶风格K-means聚类与识别方法研究＊

李经纬 赵治国 沈沛鸿 郭秋伊

（同济大学新能源汽车工程中心,上海201804）

主题词：驾驶员 驾驶风格K-means聚类 识别HEV

1 前言

驾驶风格（Driving Style）用来表征驾驶员在实车运行环境中对车辆操作的行为特征，通过对驾驶员操作习惯和汽车行驶数据的分析，动态识别出驾驶员的驾驶风格，并对控制参数进行自适应调节，对于改善车辆的燃油经济性有重要意义[1]。

国内外学者对于驾驶风格的识别进行了相关研究，如，Constantinescu等[2]应用主成分分析和分层聚类分析方法对驾驶风格进行分类和识别；Aljaafreh等[3]设计了模糊推理系统，将在一定长度时间窗中的车辆纵向加速度和横向加速度的欧式范数以及平均车速作为输入，实现了驾驶风格识别；Nadezda等[4]利用K最近邻算法、神经网络、决策树、随机森林等方法对驾驶员风格进行了识别，并对各种识别方法准确度进行了比较；Meiring等[5]对在驾驶风格识别中用到的人工智能算法进行了总结，指出模糊逻辑推理系统、隐马尔可夫模型和支持向量机在驾驶风格识别方面有更好的应用前景。

上述研究大多只针对单一车型，并没有对驾驶风格识别方法在不同车型上的通用性与适应性进行研究。为此，本文设计了基于K-means的驾驶风格识别方法，并采集了商用车与乘用车行驶数据，验证了所提出的方法对于不同车型识别的有效性。

2 不同车型驾驶风格识别的数据采集

为研究基于K-means聚类的驾驶风格识别方法对于不同车型的有效性，采集了不同驾驶员所驾驶的商用车和乘用车的行驶数据。

商用车选择了上海市浦东993路混合动力公交车，该车从东昌路渡口站出发，经过58站到达德翔路新德西路终点站，全程38 km，包含城市公路及内、外环城市快速路等多种复杂路况。乘用车选择了重庆市某混合动力（HEV）车型，在市区、郊区、高速、拥堵、通畅等不同路况下，分别由不同驾驶风格的3位专业驾驶员操控汽车完成试验。采集的部分原始数据如图1所示。

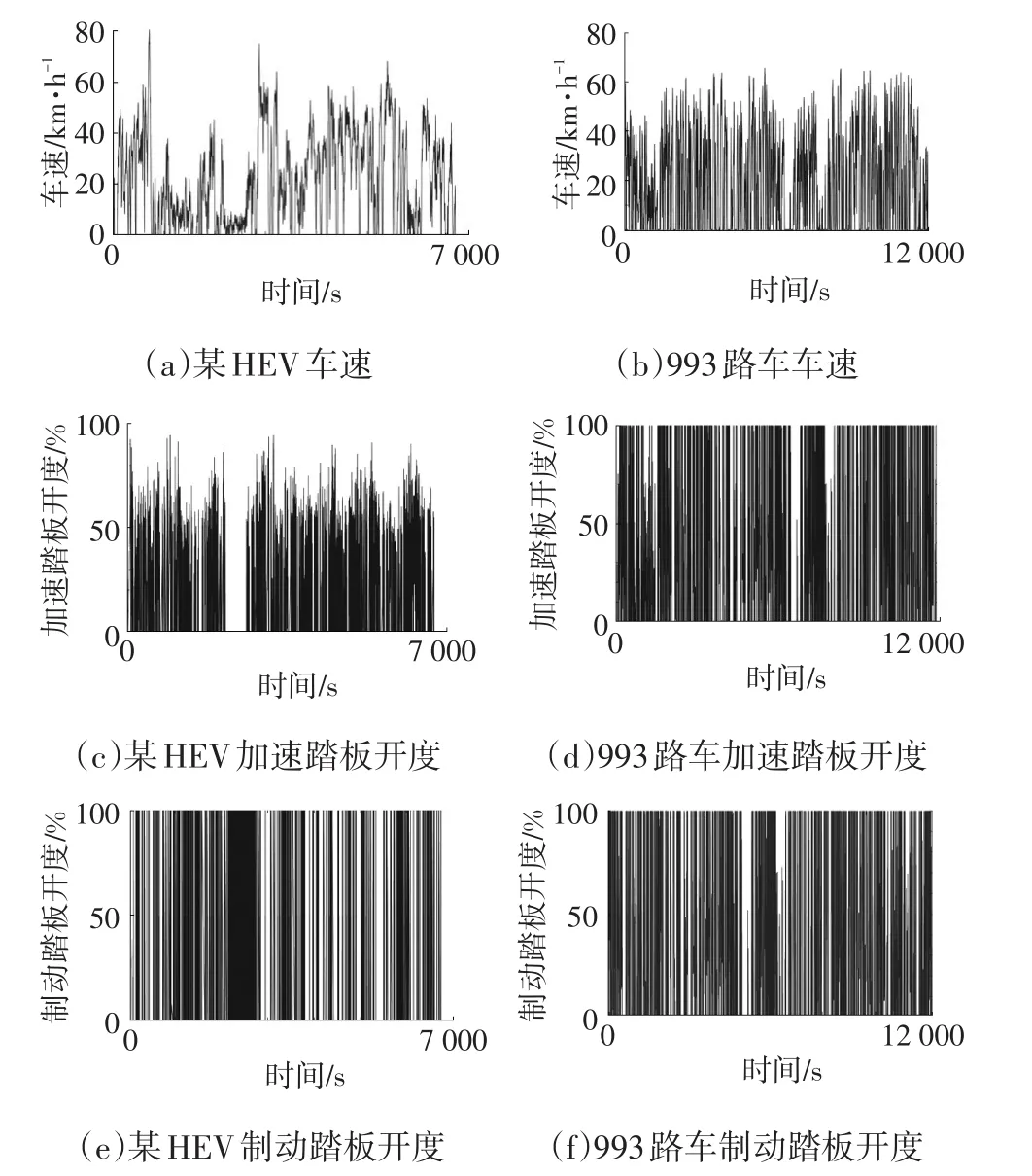
图1 采集的部分原始数据

由图1可看出，原始车速、加速踏板开度和制动踏板开度波动频率较大，数据包含高频噪声，同时个别点加速度值超过了汽车的合理加速度范围，这些点是异常点。为此，通过离群点检测[6]进行数据清洗，使用滑动均值滤波法[7]滤除原始数据中的噪声，数据预处理前、后的车速和加速踏板数据如图2所示。由图2可看出，预处理后的曲线没有异常点，可用于进一步的分析。

3 驾驶风格特征参数构建与主成分分析

在进行驾驶风格识别前，需要构建驾驶风格特征参数，用以对各识别片段的驾驶风格进行描述。构建的驾驶风格特征参数通常是一些与行驶信息有关的统计量，数目较多且彼此间存在相关性，需要使用主成分分析方法对其进行降维处理。

3.1 特征参数构建

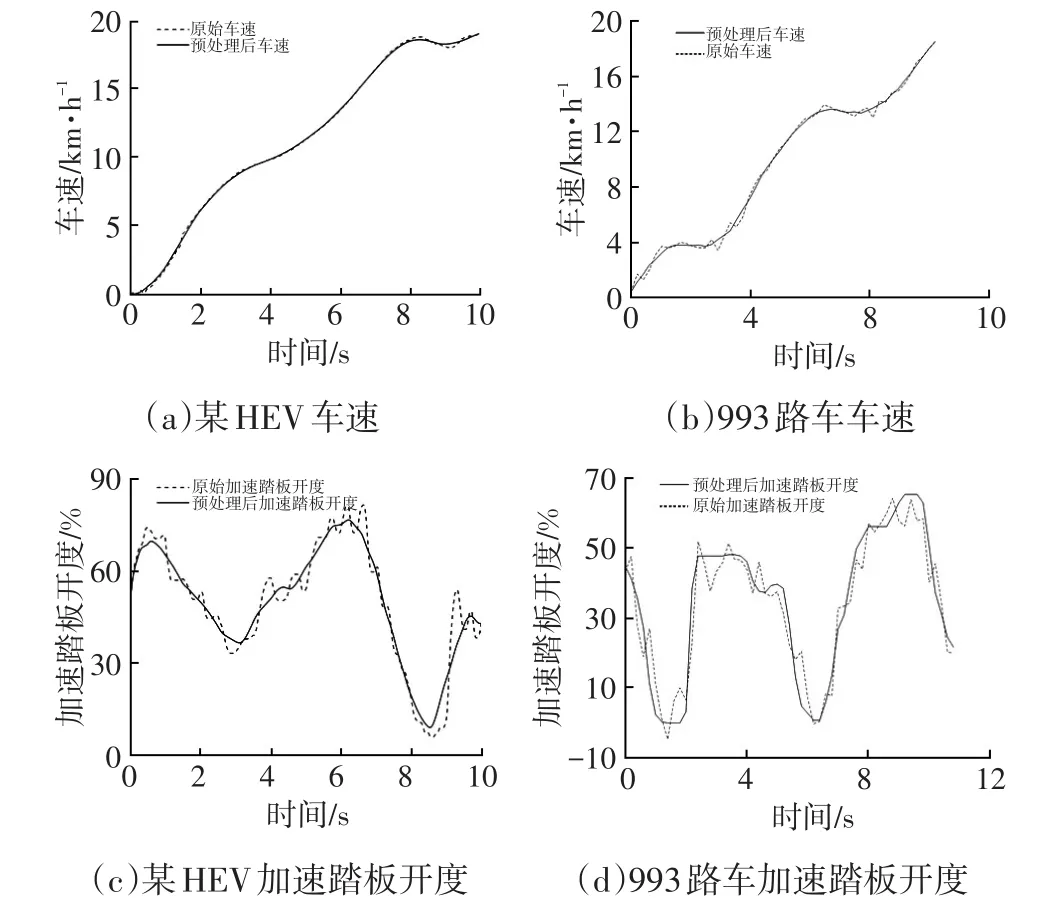
图2 车速与加速踏板开度滤波前、后对比

采集得到的数据均为连续数据，为获得更好的聚类效果，需要对原始数据进行特征参数构建。构建的特征参数不能太少或太多，为此，综合相关文献[1，2，8]选取了10个具有代表性的特征参数，见表1。

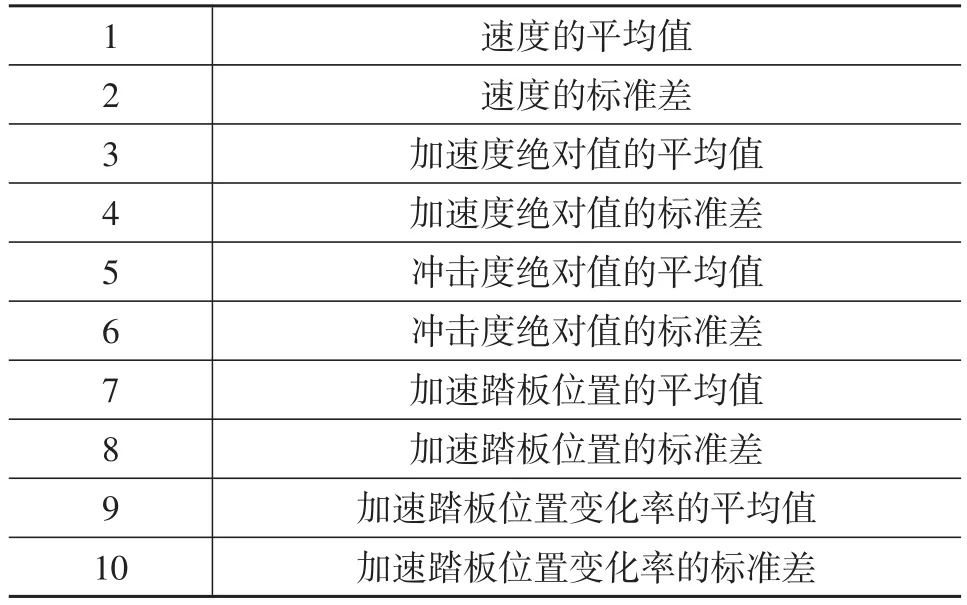
表1 特征参数

在计算特征参数时，需要确定驾驶风格识别周期的长度[9]。根据经验[8，9]，设定驾驶风格识别周期为 8 s，并对原始数据进行识别片段的划分，其中每个识别片段长度等于驾驶风格识别周期长度。

3.2 主成分分析

主成分分析是统计学中常用的降维方法，它通过构造原变量的线性组合，将原来众多具有相关性的变量化为少数几个相互独立的综合变量，同时尽可能多地保留原数据的信息[10]。在主成分求解之前，为消除量纲的差异，必须对其进行标准化处理，将每个特征参数对应的数据都变成均值为0、方差为1的高斯分布。

定义识别片段矩阵为：

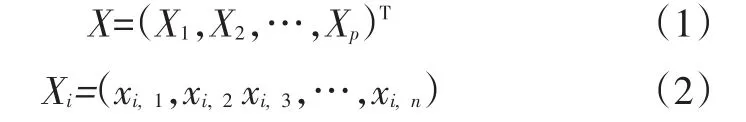
将识别片段的特征参数矩阵标准化后得到标准矩阵：

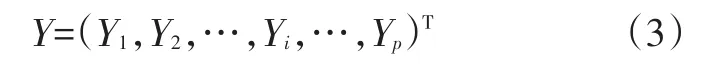
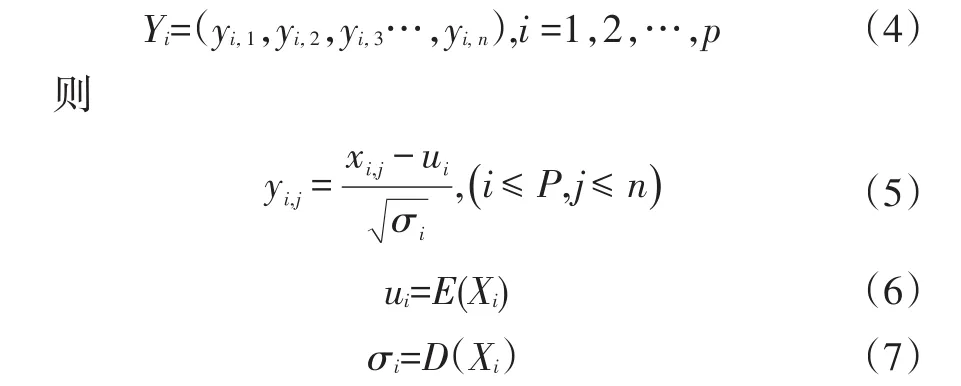
式中，i为标准矩阵（特征参数矩阵）的行下标；j为标准矩阵的列下标；p为行数，代表特征参数的数目，为10；n为列数，代表按驾驶风格识别周期划分的片段数;E为期望运算符;D为方差运算符。

对特征参数进行主成分分析，首先建立标准矩阵Y的系数矩阵：

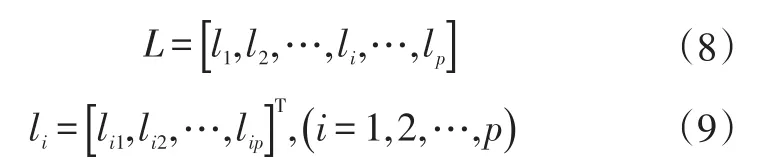
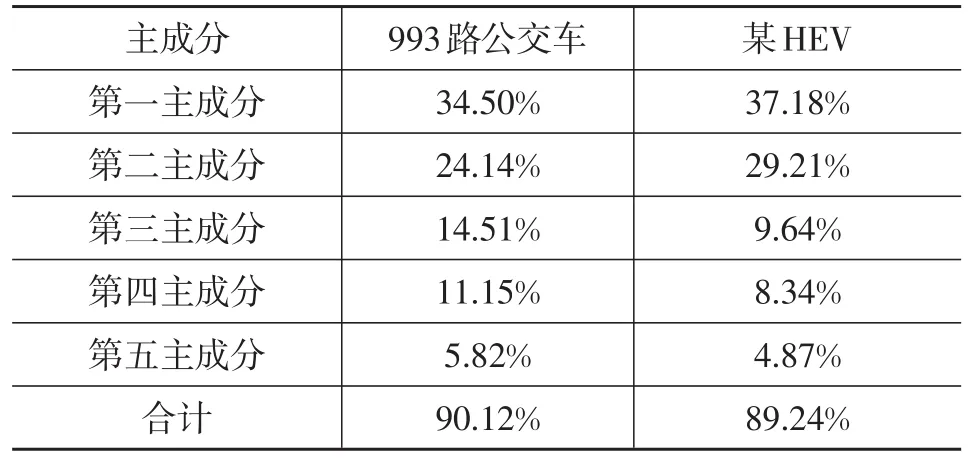
表2 两种车型统计值主成分分析结果

4 基于K-means聚类的驾驶风格识别方法

4.1 K-means方法介绍

K-means聚类算法采用距离作为相似性的评价指标，从初始聚类中心开始交替进行分配步和更新步直至聚类完成。在分配步中，将每一个观测量分配到对应的类簇，使得所有的观测点到其对应聚类中心的欧氏距离之和最短；在更新步中，用分配步得到的结果计算新的聚类中心，当聚类中心收敛时聚类结束[11]。K-means聚类方法对驾驶风格识别流程如图3所示。

4.2 驾驶风格分类

在进行驾驶风格识别前需要对驾驶风格进行分类。因驾驶风格是驾驶员在实车运行环境中对车辆操作的行为特征[1]，其分类数目与车型无关，因此利用K-means聚类方法对重庆市某HEV乘用车试验数据进行聚类分析，并确定合理的分类数目。为确定驾驶风格类型，将样本数据分别聚成2类、3类和4类，不同聚类数目的驾驶风格识别结果如图4所示。

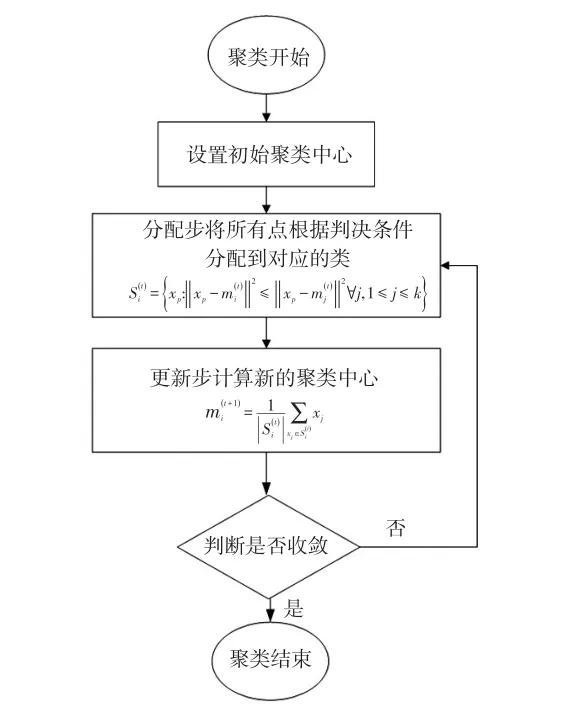
图3 K-means聚类方法对驾驶风格识别流程

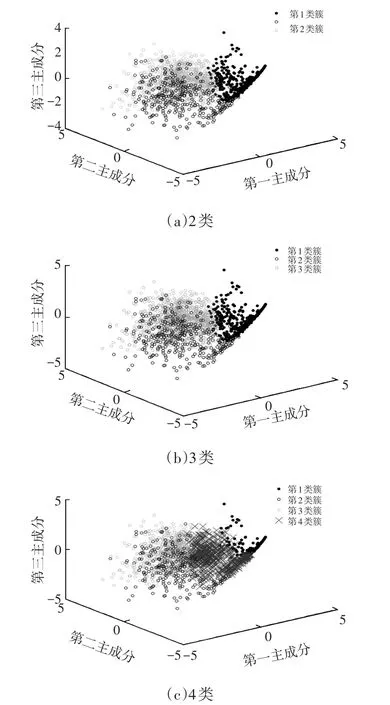
图4 不同聚类数目的驾驶风格识别结果

由图4可看出，随着聚类数目的增加，不断有新的类簇从旧的类簇中产生，同时原有类簇之间的界限也发生了变化。对各类簇所对应样本的变化进行了统计，结果如表3所列。

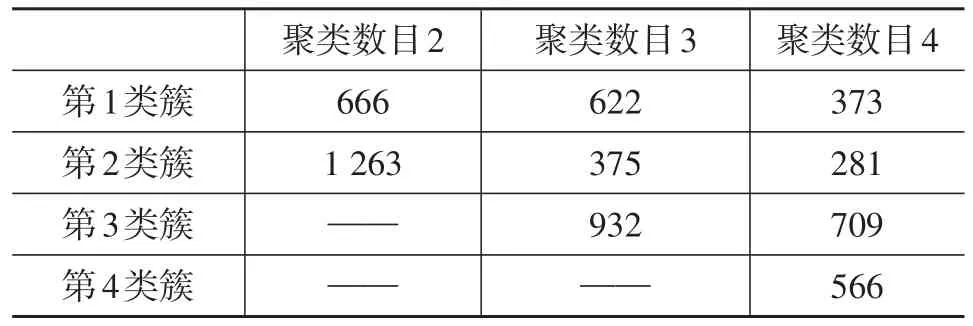
表3 样本数目随聚类数目的变化

当聚类数目为2时，两类簇样本数目差别巨大，第2类簇内的样本数目达到总样本数目的65.47%，比例超过了50%。这是因为所选的聚类数目偏少，分类不充分导致的欠分类问题；聚类数目为3时，各类簇样本数目的差距开始变小；聚类数目为4时，各类簇样本数目的差距继续变小，但第2类簇内样本数目占总样本数目的比例已不足15%，这是由于聚类数目过多带来的过分类问题。

为了研究驾驶风格分类中的欠分类与过分类问题，对随着聚类数目的变化各类簇间样本数目的转移进行了统计，如表4和表5所示。

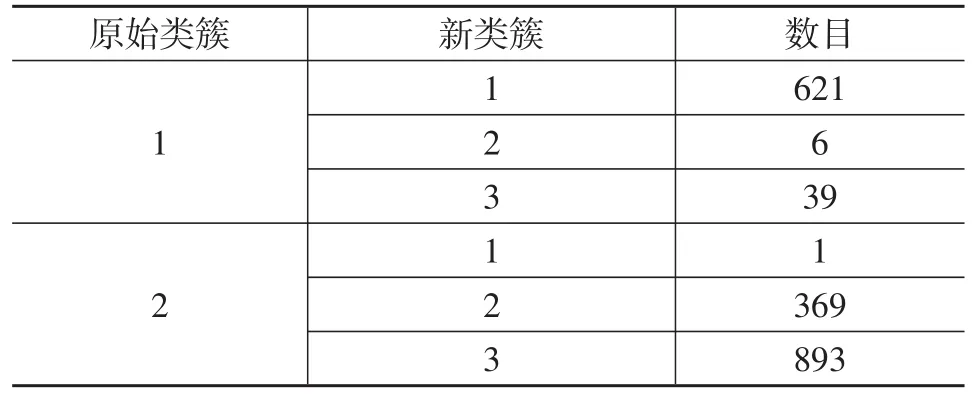
表4 聚类数目从2变化到3时样本在类簇间的转移结果

由表4可知，当聚类数目从2变为3时，第1类簇的样本数目略微下降，有少量属于第1类簇的样本被分到了第3类簇，同时第1类簇与第2类簇间的界限几乎没有变化，第2类簇内超过60%的样本被分到了新出现的第3类簇中，占第3类簇总样本数的96%。因此聚类数目为2时无法充分分类，存在欠分类。

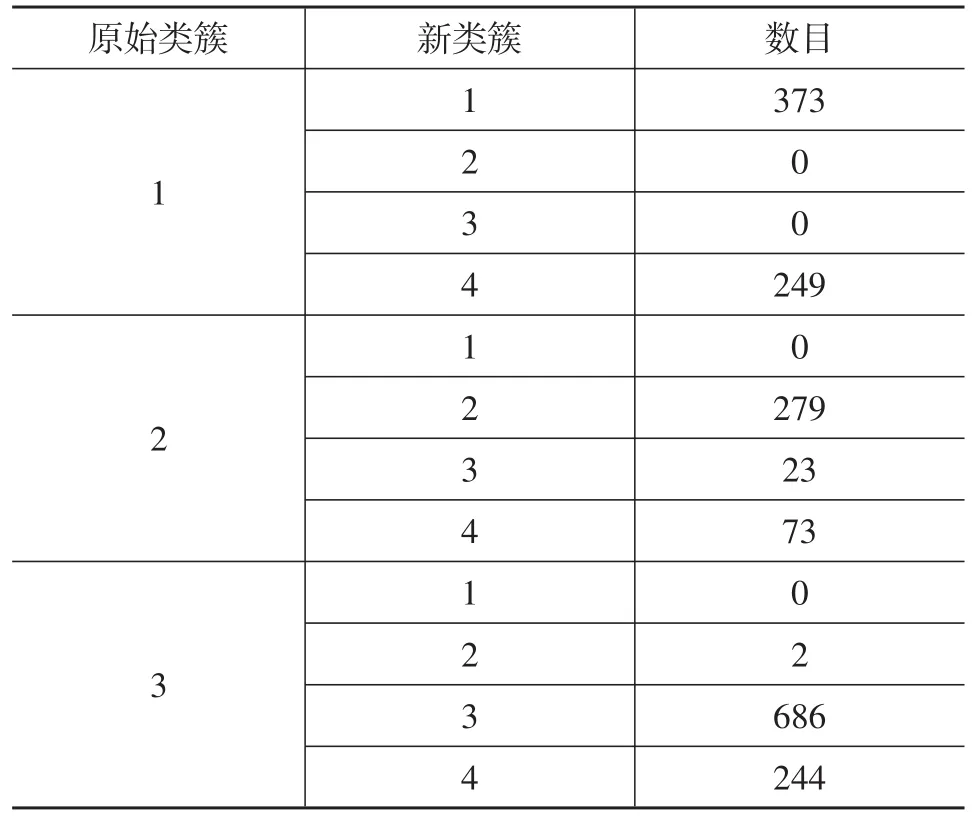
表5 聚类数目从3变化到4时样本在类簇间的转移结果

由表5可知，当聚类数目从3变到4时，原第1类簇、第2类簇和第3类簇包含的样本数均有大幅下降。其中第1类簇损失的样本全部流向了第4类簇；第2类簇的损失样本主要流向第4类簇；第3类簇损失的样本也主要流向了第4类簇。因此第4类簇的产生与第3类簇的产生有本质的不同，是明显的过分类，其样本来源于前面所有的类簇，且较大地改变了第2类簇与第3类簇间的界限。

综上所述，驾驶风格分为3类具有较好的分类效果，且各类簇具有合理的样本数与清晰的界限。

4.3 驾驶风格识别

利用K-means聚类算法将驾驶风格分为3类，则993路公交车的驾驶风格识别结果如图5所示，重庆市某HEV的驾驶风格识别结果如图6所示。

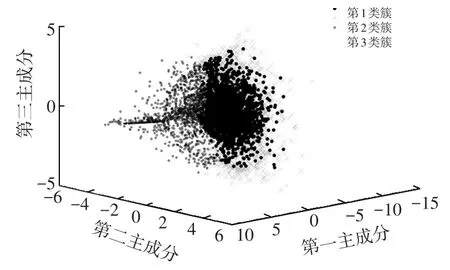
图5 993路公交车的驾驶风格识别结果

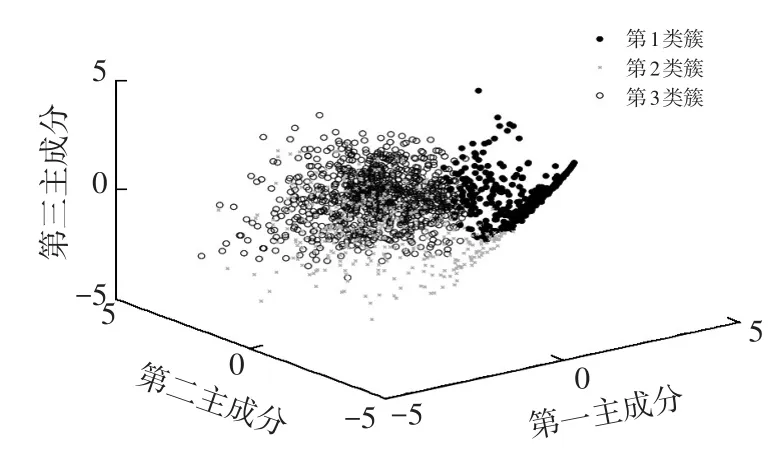
图6 重庆市某HEV的驾驶风格识别结果

由图可看出，两种车型的行驶数据被清晰地分为3类，这表明对于不同车型的行驶数据，K-means聚类方法都可以实现驾驶风格的有效识别。

4.4 识别结果分析

前述分析中将驾驶风格分为了3类，但没有将驾驶风格识别结果与人们对驾驶风格的定性认知结合起来。根据相关文献[1,2，4，5，8]，按照驾驶员驾驶车辆激进程度的从弱到强将驾驶风格定性分为冷静型、普通型和激进型3种。经计算，两种车型对应3种驾驶风格的驾驶特征参数均值如表6所列。

由表6可知，对于商用车，在3种驾驶风格中，从冷静型到激进型，加速度均值、加速度标准差、冲击度均值、冲击度标准差都是从小到大，这与越激进的驾驶风格越倾向于急加速和急减速的定义一致。因此用KMeans聚类对商用车驾驶风格进行识别是合理的。对于乘用车，加速度与冲击度的相关参数是3种驾驶风格的重要特征，它们数值越大表征驾驶风格越趋向激进型，这与993路公交车数据得到的结论一致，因此基于K-means的驾驶风格识别方法对乘用车同样有效。

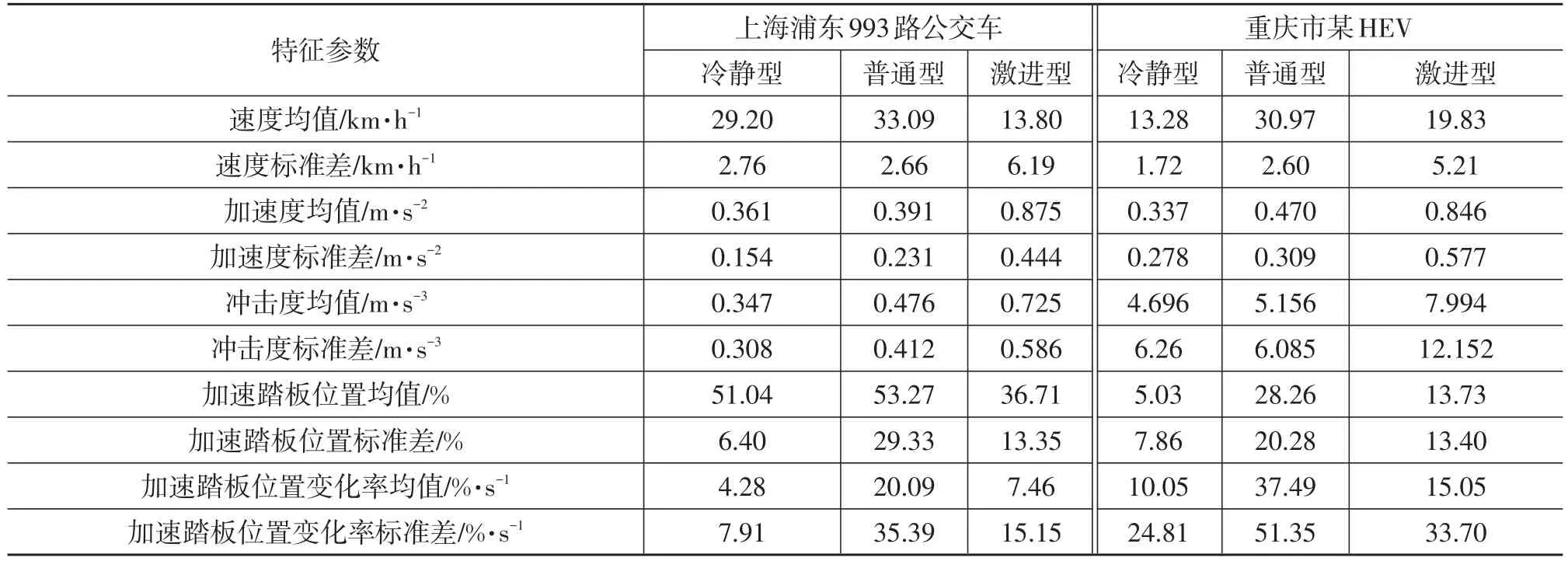
表6 两种车型对应3种驾驶风格的驾驶特征参数均值

5 结束语

为研究驾驶风格识别方法，采集了上海市浦东993路公交车和重庆市某HEV实际运行数据，参考已有研究构建了10个特征参数并确定驾驶风格识别周期为8 s。综合使用主成分分析和K-means聚类方法对驾驶风格进行了识别，结果表明，将驾驶风格分为3类具有较好的聚类效果，且基于K-means的驾驶风格识别方法对乘用车和商用车均具有较好的识别效果，也进一步表明了该方法的通用性和有效性。