车载网中一种低延时的广播路由＊

杨茂保 徐利亚 葛明珠 舒长兴

（九江学院，九江332005）

主题词：车载网 紧急信息 广播路由

1 前言

车载自组织网络（Vehicular Ad hoc Network，VANET）是一种将传感器技术、短距离移动通信及信息处理技术相结合的移动自组网（Mobile Ad hoc Network，MANET），是智能交通系统的基础信息承载平台。VANET中的节点主要由车辆组成，车辆可利用车载传感器实时采集交通信息，通过与其他车辆的交流来广播安全、道路状况等信息，在改善交通环境、减少交通事故等方面具有积极的作用[1]。此外，在VANET中，车辆还可以与路侧单元（Road Side Units，RSU）通信，通过RSU接入主干网，为车内成员提供更丰富的服务[2-5]。

车载网中的广播路由算法主要有基于地理位置的路由[6-9]、基于内容的路由[10-14]。基于地理位置的广播路由算法的优点是实现较简单、执行效率高，通常基于地理位置划分候选节点，选择距离广播节点更远的节点作为下一跳中继节点来转发数据包，但该类算法没有很好地顾及到VANET中车辆节点移动速度快、网络拓扑变化快的特点，当数据包传输到车辆节点稀少的路段时，会产生极大的延时。基于内容的广播路由算法中，数据包含有本地拓扑信息，能高效率地选择中继节点来传输数据包，但由于拓扑变化快，会产生冗余，当节点缓存已满时会造成数据包的丢失。

因此，信息在车载网络中的传输面临诸多挑战：节点密度大、车速快使得网络拓扑结构变化极快，节点间形成的链路持续时间较短；节点的移动受道路的强制约束，使得网络中节点分布不均匀，造成VANET中严重的网络分割现象；在道路区域，特别是热点区域（如交叉路口周围），节点的密度巨大，如不加限制地使所有节点自由广播信息，会带来激烈的信道资源竞争，使得该区域的无线传输瘫痪。这些因素导致信息在VANET中的传输不稳定，本文提出一种低延时的广播路由，通过建立连通支配集，概率广播数据包来减少传输冲突。

2 单位圆盘图

本文讨论的VANET场景采用全向传输方式。根据全向传输方式中无线覆盖区域呈圆盘状的特点，该区域可用单位圆盘图（Unit-Disk Graph，UDG）[15]表示，即G=(V,E)，其中，V为节点集，E为边集，即两点之间可形成链路。

以发送节点的位置为圆心，以无线通信最大传输范围为半径，且假设节点的最大无线传输范围相同，如果节点在另一个节点的通信范围内，则这两个节点可以通信，即它们之间存在一条链路。

在UDG模型中，每个节点都有唯一的ID以标识身份。|V|表示网络中节点的数量，|S|表示任意节点集合S⊆V(G)中节点的数量，|E|表示边的数量。以(vi,vj)∈E(G)表示节点vi和vj有直接连接的边，即vi与vj相邻，节点vi和节点vj互为邻居节点。

连通支配集（Connected Dominating Set，CDS）是圆盘图G中的节点集合D⊆V(G)，对任一节点v，v∈U或者v是D中节点的邻居节点。

若v是图G中的一节点，集合Neighbor(v)表示v的邻居集。

d(u1,u2)为顶点u1、u2之间的距离，R为节点最大传输距离，如果d(u1,u2)＜R，则顶点u1和u2有一条连通的边。

U是节点内维护的集合，存放当前节点为中心长度为d的路段内的所有节点。

3 路由选择

本文提出的广播路由方法为：对VANET热点区域中的车辆节点构造CDS；对每个要传输的数据包，选择CDS中的节点作为广播路由的中继车辆节点，并按一定的概率广播。

3.1 连通支配集的构造算法

车辆节点的传输模型是UDG，然而在图中，计算最小连通支配集（Minimum Connected Dominating Set，MCDS）是不确定多项式时间问题（Non-deterministic Polynomial-time hard，NP-hard）[16]，即在多项式时间内不收敛，得不出解。本文研究该问题的近似解，即构建一个近似最小的CDS算法。

3.1.1 算法描述

构建以当前节点S为中心的通信范围内初始连通图G(V,E)，用最小生成树思想[17]构造1个初始CDS。要使CDS内的节点数更少，则要保证选入CDS内的节点具有更多的邻居节点，构建M-CDS。在图G(V,E)中，当前节点的邻居节点数即为该节点的度，所以在选择CDS内的节点时，将节点的度作为权衡参数，节点的度越大，其权值越高。

3.1.2 算法实现

构建VANET中以源（source）节点为中心，长度为d的区域内的CDS，并将该CDS广播到区域内的所有节点。构建的初始图G(V,E)算法和M-CDS算法流程分别如图1、图2所示，其中，u0为source顶点，CDSinitial为初始连通支配集。

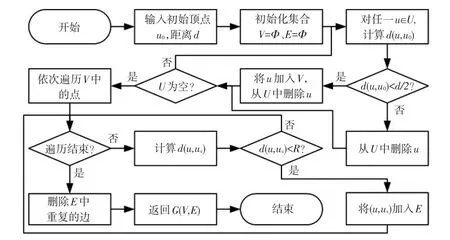
图1 初始图G(V,E)算法流程

图2 M-CDS算法流程

3.1.3 算法分析

初始图G（V，E）算法是依据数据结构中经典的构造图方法建立的，时间复杂度为O(n3)。M-CDS算法的时间复杂度分析过程为：

a.赋权值给图中的各边，其时间复杂度为O(n)。

b.Prim算法生成最小生成树的时间复杂度为O(n2)。

c.选择非叶子节点。对于构建好的最小生成树中的节点，易知只需依次判断节点的度是否为1即可，故该部分的时间复杂度为O(n)。

d.去除冗余的节点。需要将初始支配集中的节点两两进行邻居节点对比。对于n个节点，两两遍历需要查询的次数是n(n-1)/2。假设两节点拥有的邻居节点数分别为m1和m2，邻居节点集中的节点以ID按序排列，则判断两节点的邻居集是否存在包含关系需要的查询次数为max{m1,m2}。在一个网络中，当每个节点拥有的邻居节点数超过5.177 4logn[18]时，该网络是全连通的，因此，m1、m2均小于5.177 4logn，则该步的时间复杂度为O(n2logn)。

由于上述步骤是顺序执行的，所以构建CDS的时间复杂度是O(n2logn)。

3.1.4 结果分析

选择经典的贪心算法（Greedy Algorithm）和Rule-K算法，在静态拓扑场景下与本文提出的M-CDS算法进行比较，然后按照VANET场景设置节点传输半径R和随机图中的节点数n，得到CDS内的节点数量与传输半径R和图中节点数n的关系，如图3所示。

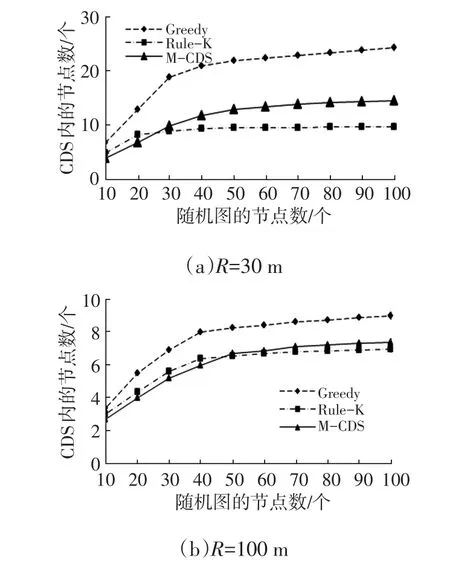
图3 CDS内的节点数量随图中节点数量的变化

由图3a可知，当R=30 m时，贪心算法生成CDS内的节点数量较Rule-K算法和M-CDS算法多。当节点数较少时，M-CDS算法的表现与Rule-K算法较为接近，但随着节点数的增多，Rule-K算法的性能略胜一筹。这是因为随着节点的增多，CDS内的节点数量随之增加，导致边界网关增多。Rule-K算法去除冗余节点的规则比M-CDS更为精确，能最大限度地得出MCDS，但是其相应的开销稍大些，相反，M-CDS算法实现简单，开销相对较小。

由图3b可知，当R=100 m时，贪心算法生成CDS内的节点数量依然较其他2个算法大，而Rule-K算法与M-CDS算法生成的CDS较为接近。这是由于节点传输半径增大使得节点邻居数大量增加，M-CDS算法生成的CDS中每个节点拥有更多叶子节点，生成初始的CDS时会删除所有的叶子节点，即删除的冗余节点也更多。

在本文场景中，选择长为10 km、宽为25 m的矩形区域，随机投放一定数量的车辆节点，每个车辆节点的连通半径为R=200 m，距离小于R的车辆节点间能够通信，反之不能通信。每次随机产生的图如果是连通的，则继续试验，否则重新产生随机图。

设R=200 m，车辆节点数量n的变化范围是10～100，对每个n，生成100次网络拓扑图，求解图中CDS内节点的数量，取平均值，结果如图4所示。

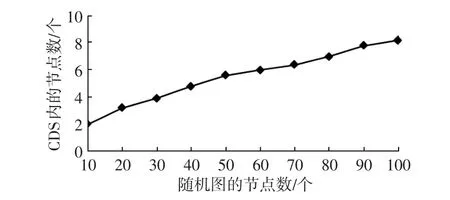
图4 R=200 m时CDS的节点数量随图中的节点数量的变化

由图4可知，CDS中包含的节点数量随图中节点数量的增加而增加，当节点数达到100时，产生的随机图已经非常稠密，但是由M-CDS算法产生的CDS所包含的节点数却较少。

设n=20，R的变化范围为100～200 m，进行100次试验，取平均值，结果如图5所示。

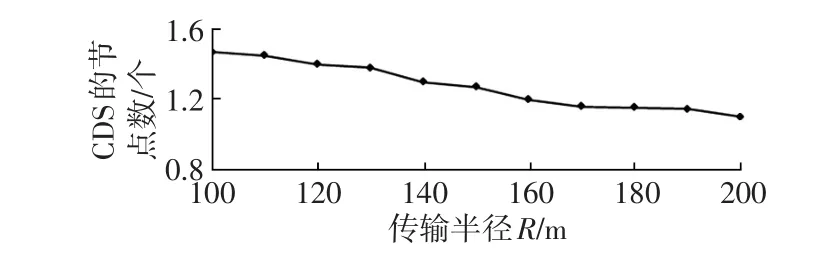
图5 n=20时CDS的节点数量随节点传输半径的变化

由图5可知，当节点传输半径增加时，CDS的数量减少，但CDS中包含的节点数量增加。当R=200 m时，CDS的数量几乎为1，因为理论上此时几乎能覆盖到区域内的所有节点。

3.2 概率广播

构建M-CDS后，本文以CDS中的节点作为广播节点来广播数据包。为了进一步减少节点的广播数据包数量、减少传输冲突、提高信道利用率，本文针对CDS中的节点，提出一种动态的按概率广播的策略广播数据包，根据节点的密度和邻居覆盖集计算节点的广播概率。

3.2.1 节点平均密度的计算

本文根据局部邻居节点信息来计算网络中局部节点的密度。如果某节点的邻居节点数比网络中节点的平均邻居节点数多，则认为该节点所处的区域是节点密度大的区域，反之是节点密度稀疏的区域。

网络中节点的平均邻居数量为：

式中，N为网络中节点的总数量；Ui为节点i的邻居数量。

3.2.2 节点的邻居覆盖集设定

本文的目标是当传输路由请求（Route Request，RREQ）包时，减少冗余包的传输，从而不影响网络吞吐量。根据节点所在区域的节点密度和广播包已覆盖的邻居节点集来动态设定当前节点广播该数据包的概率。节点根据接收到的RREQ包中的节点信息更新自己的邻居节点表，并确定该RREQ包已覆盖的邻居节点集。如果当前节点的一跳邻居节点已经有相当部分被该RREQ包覆盖，则当前节点广播该RREQ包的概率较低。

节点的数据包覆盖邻居集指已经接收到同一个数据包的该节点的一跳邻居节点集。如图6所示，节点S将RREQ包广播到它的邻居节点A、B、C、D、E，由于节点C和节点E是D的邻居节点且已经收到了同样的RREQ包，所以对于该RREQ包，D的邻居覆盖集就是节点C和节点E。

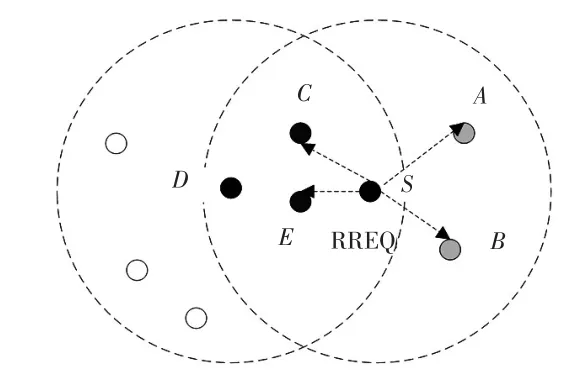
图6 节点的数据包覆盖邻居集示意

3.2.3 节点广播数据包的概率

M-CDS构建完毕后，根据前文的结果计算数据包被当前节点u广播的概率：

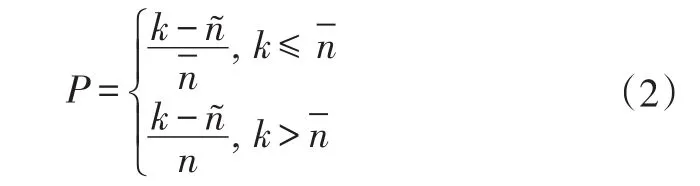
式中，ñ为当前节点的邻居覆盖集中的节点数量；k为当前节点的邻居节点数。

4 性能评估和分析

对数据包从当前节点广播到目标区域中所有节点时所产生的延时和数据包的递送率进行仿真测试，参数设置如表1所示。

首先将本文提出的低延时广播路由（Low Latency Broadcast Routing，LLBR）与最基本的洪泛广播进行比较，数据包生成率为10个/s，结果如图7所示。

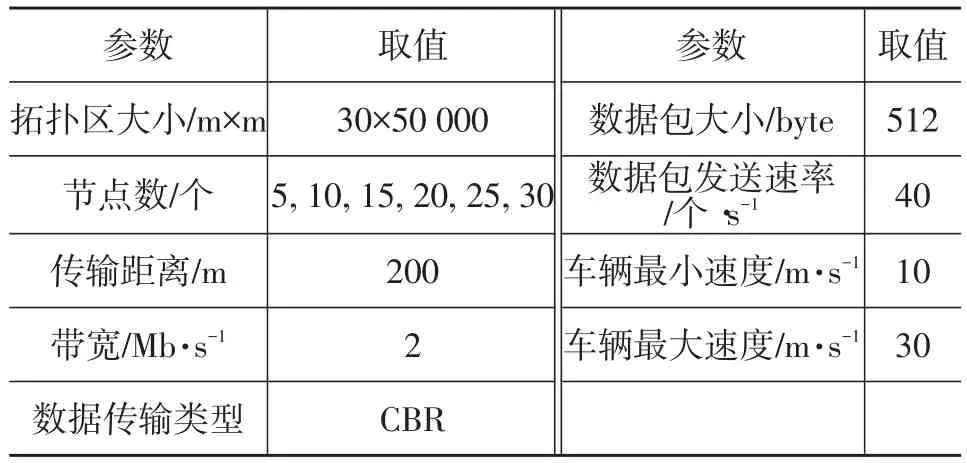
表1 仿真参数

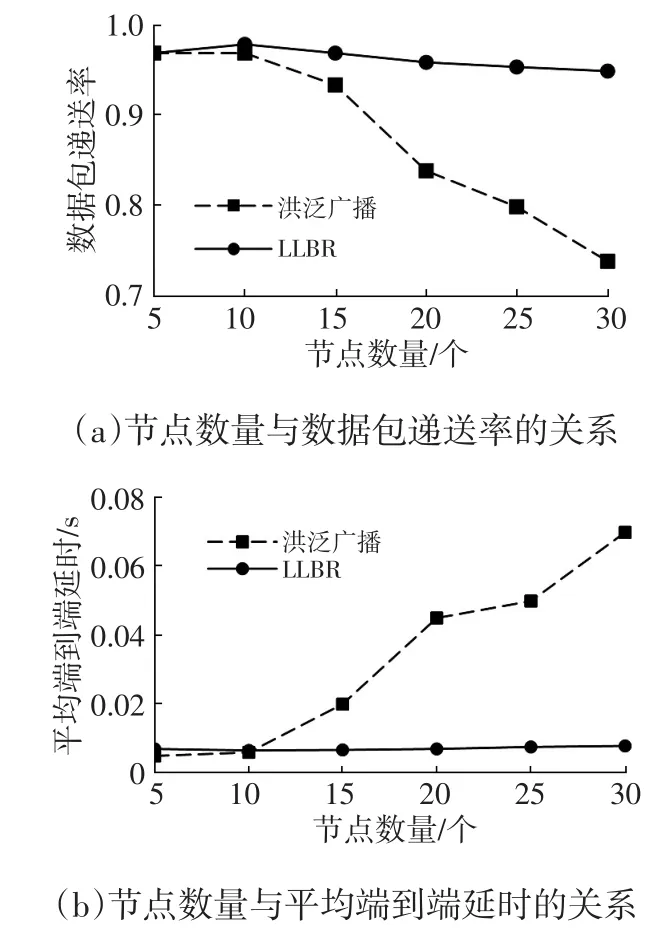
图7 LLBR与洪泛广播的仿真结果

由图7可知：当节点数量较少时，两种方法的数据包递送率都接近为1，洪泛广播的平均端到端延时小于本文所提出的广播方法；随着热点区域中节点数量增多，洪泛广播中的数据包递送率下降明显，而本文提出的广播方法递送率仍接近1，洪泛广播产生的平均端到端延时几乎呈线性增加，而本文提出的广播方法产生的延时增加不明显。节点数量少时，广播的数据包较少，不会产生传输冲突，所以递送率高；节点数量增加时，洪泛广播中每个节点都广播所接收到的数据包，数据包数量呈指数增加，所产生的冲突急剧增多，造成数据包的丢失增多，端到端延时也急剧增加，而本文提出的广播方法构建区域中的CDS，通过支配集中的节点对数据包进行概率广播，极大地减少了广播的数据包数量，递送率和端到端延时与节点数较少的场景无明显差异。

将本文提出的方法与基于邻居覆盖的概率转发（Neighbor Coverage-based Probabilistic Rebroadcast，NCPR）广播算法[19]和基于距离的多跳广播（Distancebased Multi-hop Broadcast，DMB）算法[20]进行比较，数据包生成率为10个/s，结果如图8所示。

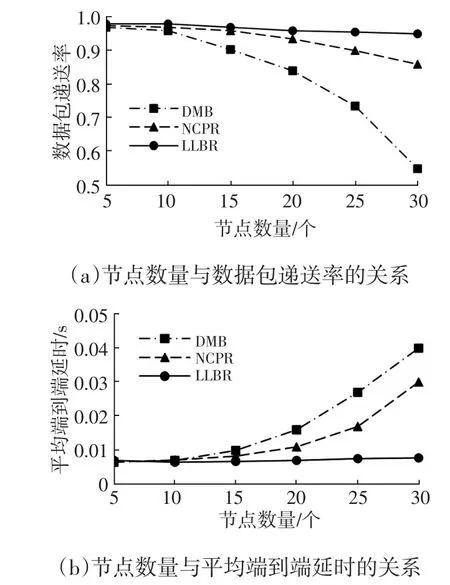
图8 LLBR与NCPR、DMB的仿真结果

基于概率的广播要求节点收到广播数据包后以一定的概率P来转发分组，其中P通常是由当前节点到前一跳转发节点的距离与它们的传输范围的比值决定的，则距离前一跳转发节点最远的节点最有可能成为新的中继节点，当P=1时，该方法等同于洪泛方法。当车辆密度较大时，很多节点具有相似的覆盖范围，因此随机使一些节点不再广播分组在一定程度上节约了网络资源。但是当车辆密度较小时，节点间覆盖范围基本不重合，除非P足够大，否则将会有一部分节点无法接收到所有广播信息。基于概率的广播的缺点是节点可能以较小或较大的概率来转发分组，造成广播分组的严重缺失或高度冗余。

基于距离的广播算法在通信范围内节点间距离d越小则额外覆盖面积越小，d越大则额外覆盖面积就越大，当d=0时，额外覆盖面积也为0，该方法利用节点间的相对距离决定是否转发分组，d可以通过GPS设备获取或者根据消息的发射和接收功率间的关系计算得出。

由于车辆速度较快，车辆间的距离变化较快，所以基于距离的广播算法性能较差。由图8a可知：节点数量较少时，3种方法的数据包递送率都接近1；当区域中的节点数量增多时，DMB中数据包的递送率下降明显，NCPR算法较DMB算法表现更好，本文提出的广播算法递送率仍接近1。由图8b可知：当节点数量较少时，DMB和NCPR算法的平均端到端延时小于本文提出的广播方法；随着节点数量增多，DMB广播产生的平均端到端延时增加明显，而NCPR算法和本文所提出的方法有较好的性能。这是因为，当节点数量较少时，网络广播的数据包较少，基本不会产生传输冲突，本文提出的广播算法需要构建CDS并计算支配集中节点的广播概率，会产生延时；当区域中的节点数量增多时，节点间相对距离减小，DMB算法的数据包数量增多，产生的冲突增多，造成重复广播的次数增加，NCPR中，随着节点数量的增加，对于相同的数据包来说，其节点的邻居节点的邻居列表中该节点未覆盖连通的节点（Uncovered Neighbors，UCN）集随之减少，使得节点广播该数据包的概率降低，即减少传输冲突，具有较好的延时，本文提出的广播算法极大地减少了广播的数据包数量和冲突的次数。

5 结束语

本文基于减少广播数据包节点数量的思想设计广播路由，对当前节点通信范围内的节点构建连通支配集，对连通支配集中的节点进行数据包概率广播，仿真结果表明，本文提出的方法极大地减少了广播数据包的节点数和广播时产生的冲突，从而减少数据包传输时的平均端到端延时，提高数据包的递送率。