基于多目标SMC汽车转向稳定性研究＊

智淑亚 刘祥建 郭语 凌秀军

（金陵科技学院,南京211169）

主题词：汽车 转向稳定性 控制器 多目标滑模控制 可变传动比转向系统

1 前言

汽车转向稳定性对提升汽车的主动安全性具有重要作用，关于汽车转向稳定性问题国内外已有很多研究，如，文献[1]在转向工况失稳特征的基础上对稳定性控制进行了研究；文献[2]提出了基于主动前转向控制的电动汽车的鲁棒偏航稳定性模糊PID策略；文献[3]利用滑模变结构控制理论设计了3种控制器，均可有效提高汽车极端工况下的操纵稳定性；文献[4]以侧滑角为控制变量，分别采用前馈和神经PID两种控制算法，通过仿真比较证明神经PID算法优于前馈控制；文献[5]选择侧滑角和横摆角速度作为稳定性控制的控制变量对电动汽车稳定性进行滑模控制。这些文献很少以侧滑角和偏航角为控制变量对汽车转向稳定性进行滑模控制，实际上前后轮胎的偏航角与侧滑角和偏航率直接相关，过度转向或转向不足都将影响汽车转向稳定性。当侧滑角很小时，汽车的动态特性由偏航率决定；严重侧滑时，侧滑角则迅速增大，仅用偏航率不能准确描述汽车的动态特性。

本文针对机械式AFS(Active Front Steering)系统提出一种基于VGRS(Variable Gear Ratio Steering)的多目标滑模变结构SMC（Sliding Mode Control）控制策略，对侧滑角和偏航率同时进行控制，以评价转向稳定性。

2 AFS系统构成及工作原理

可变传动比的机械式AFS系统安全性和可靠性较高，应用广泛，其由VGRS执行器、VGRS电子控制单元(ECU)、信号传感器、转向盘、转向柱、转向轴、小齿轮与齿条传动装置组成，如图1所示。

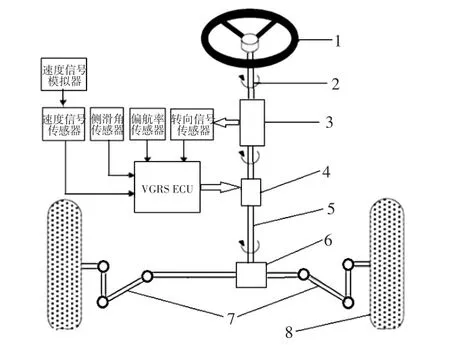
图1 AFS系统结构示意

VGRS系统由控制器和执行器组成。控制器由转向控制单元ECU根据信号传感器控制VGRS执行器，基于转角传感器和车速传感器信号计算执行器工作角，以操纵直流电机，同时控制器通过信号传感器可获得汽车速度、转向、侧滑等信号。若执行器选择合适的工作角度，VGRS则通过控制器和执行器使汽车获得合适的转角。VGRS执行器可靠性高、响应快，主要包括减速机构、直流电机和锁止机构等，其结构如图2所示。减速机构由定子齿轮、从动齿轮、柔性齿轮、波发生器等组成，波发生器与柔性齿轮的传动比为50∶1。

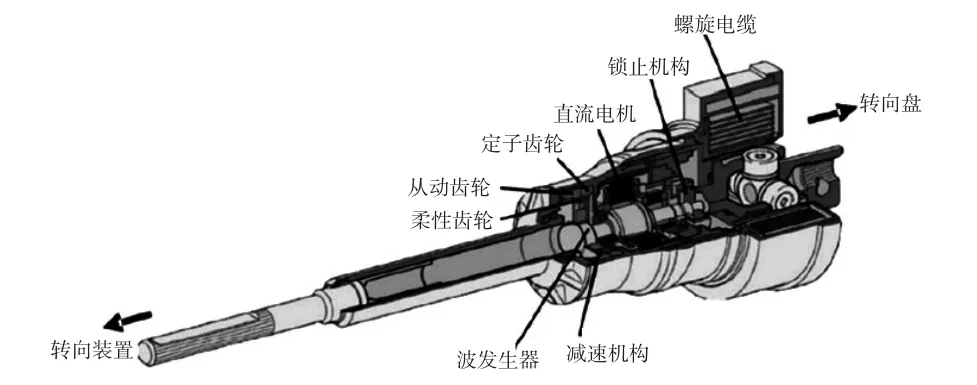
图2 VGRS执行器结构

VGRS执行器根据汽车行驶速度有如下3种工作状态：

a.当顺时针转动转向盘（右转向）时，VGRS ECU接收到信号，然后由控制器处理并发出指令到直流电机，电机驱动波发生器旋转。若车速较低，直流电机则逆时针旋转，此时波发生器的转向与转向盘相反，通过波发生器将传动输入到减速机构，驱动柔性齿轮和从动齿轮工作。此时波发生器旋转50转，柔性齿轮仅旋转一圈，从动齿轮随之旋转一圈，其转向与转向盘相同，通过从动齿轮使输出轴产生顺时针转角，其大小等于转向盘实际转角与VGRS执行器总成转角之和，即增加了输出转角，表明汽车转向响应加快，可防止汽车转向不足。

b.当转向盘右转向时，若车速较高，则直流电机顺时针旋转，此时波发生器与转向盘转向相同，驱动柔性齿轮和从动齿轮，从动齿轮与转向盘转向相反，输出轴转角等于转向盘实际转角减去VGRS执行器总成转角，即减小了输出转角，表明汽车转向响应减缓，可防止汽车转向过度。

c.当VGRS执行器发生故障时，锁止机构锁定电机，避免产生不利后果[6-7]。

3 VGRS执行器数学模型

根据VGRS的工作原理，当波发生器与定子齿轮以相同方向旋转时，输出轴转角将随着波发生器的正转角而增大；反之，当波发生器与定子齿轮以相反方向旋转时，输出轴转角将随着波发生器的负转角而减小；当直流电机没有动作时，输出轴转角等于定子齿轮转角。减速机构中从动齿轮的角速度等于定子齿轮与柔性齿轮角速度之和，而输出轴角速度与从动齿轮角速度相同，由于转角与角速度成正比，故输出轴转角可表示为:

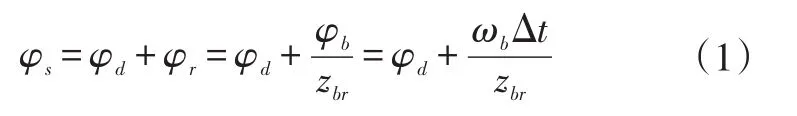
式中，φs、φd、φr、φb分别为输出轴转角、定子齿轮转角、柔性齿轮转角、波发生器转角；ωb为波发生器的角速度；zbr为波发生器与柔性齿轮的传动比；Δt为控制器输出转角与实际前轮转角输出的时间差。

通过转向装置输出的实际前轮转角可表示为:

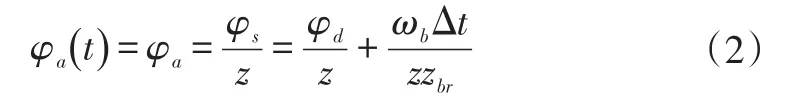
式中，φa(t)为实际前轮转角；z为转向系统的传动比。

因控制器输出转角与实际前轮转角存在时间差Δt，故控制器输出转向角φk(t)与实际前轮转向角φa之间的关系可表示为:

式中，t为工作时间。

4 AFS系统控制器设计

4.1 汽车控制模型

为了分析汽车转向系统的动力学特性，建立二自由度（2-DOF）汽车简化模型，如图3所示。

设4个车轮均采用线性轮胎模型，两个前轮的转向角、侧滑角与两后轮的转向角、侧滑角分别相等，两个前轮轮胎的侧偏刚度与两后轮的轮胎侧偏刚度分别相等。根据图3所示，通过直接横摆力矩控制，以保证其转向稳定性，则汽车模型的动力学方程[6]为：

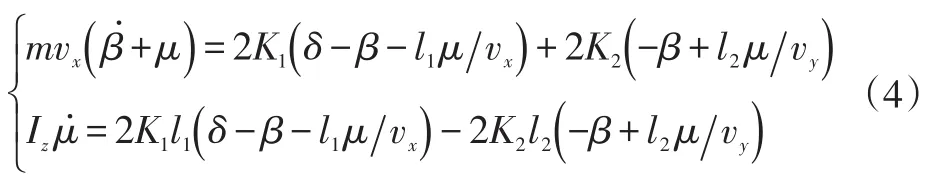
式中，m为汽车质量；β为汽车侧滑角；μ为汽车偏航率；δ为前轮转向角；l1、l2分别为质心到前后轴的距离；vx、vy分别为质心横向和侧向速度；Iz为汽车绕z轴的转动惯量；K1、K2分别为前、后轮的侧偏刚度。

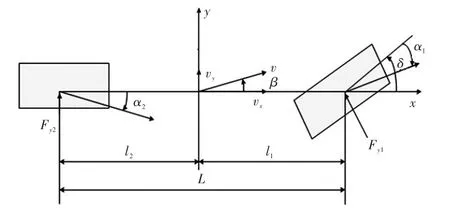
图32 -DOF汽车模型

由式（4）可得汽车模型的状态方程为：

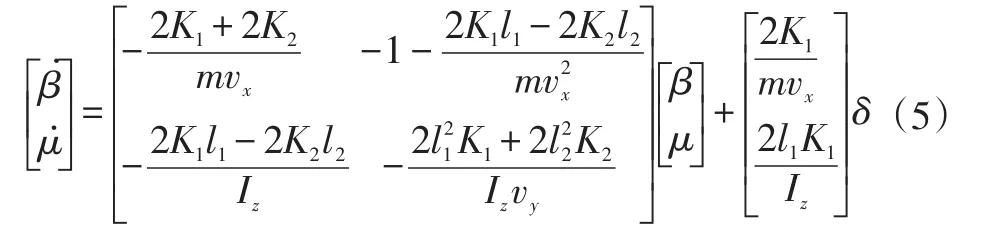
4.2 滑模控制变量及其误差

控制器对提供转向稳定性、增强AFS系统的鲁棒性起着关键作用，而侧滑角和偏航率是衡量汽车稳定性的两个重要状态变量。滑模控制算法较简单、响应时间短、抗干扰能力强，考虑汽车实际运行时的响应速度及抗干扰需求，这里选用此算法对侧滑角和偏航率进行控制。

假设汽车在稳态条件下行驶，侧滑角和偏航率是稳定的，由式（1）可知，β和μ具有一定耦合关系,利用滑模控制理论，同时控制这两个变量，可以解决单独控制μ时β过大以及单独控制β时不能很好地跟踪理想μ的问题。

汽车的参考模型可表示为：

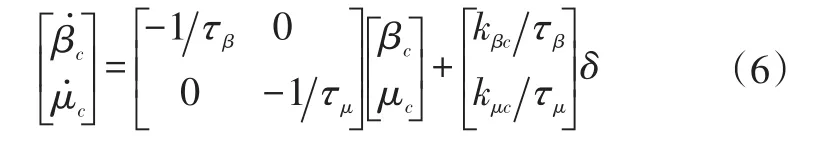
式中，βc、μc分别为侧滑角、偏航率的期望值；τβ、τμ为时间常数，取0.2；kβc对应βc稳态增益，kβc=0，kμc对应μc稳态增益。

将上式写作状态表达式:

式中，Xc为状态向量；Yc为控制输入向量；Ac、Bc均为2×2矩阵。

侧滑角和偏航率实际值与期望值之间的误差e可表示为:

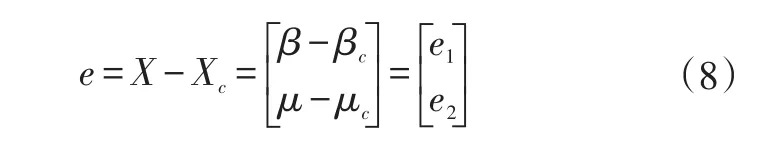
则误差变化率为:

式中，A和B分别为状态变量矩阵和控制输入矩阵。

4.3 SMC控制策略

趋近运动是提高转向系统动态性能的关键环节。滑模变结构控制的趋近率包括等速趋近率、指数趋近率、幂次趋近率和一般形式趋近率。为了实现滑模变结构的滑模运动，有效削弱抖振，这里采用指数趋近率，并利用SMC策略对侧滑角和偏航率进行联合控制，在方程(4)描述的线性系统中定义滑模面[7]为：

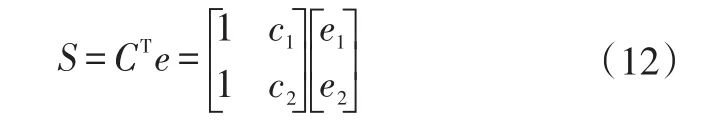
式中，S为侧滑角和偏航率的滑模变量；e1、e2分别为侧滑角和偏航率的跟踪误差；C为切换面；c1、c2分别为联合控制权值系数，均为正值，只要取值合适，则可使系统运动形态受控，在期望时间内可到达设定的滑模面。

指数趋近率为：

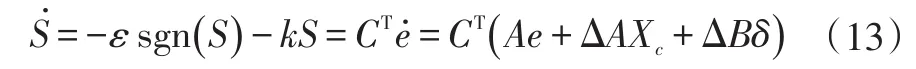
式中，ε为趋近切换面的速率；k为指数项系数。

为进一步防止抖振，由sat(S)代替比例项，定义为:

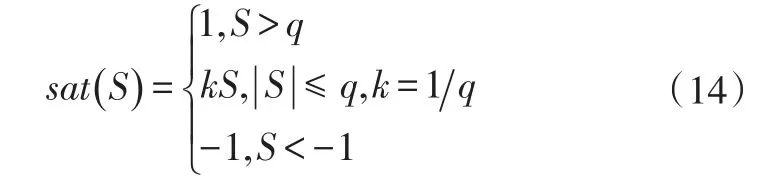
式中，k为常数；q＞0为边界层，可以根据高频抖振情况选取适当的边界层厚度。

滑模控制的控制律可设计为:

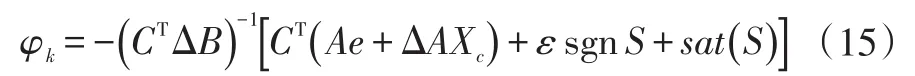
式中，φk为控制器输出转向角。

控制器的AFS工作角度(即在前轮上的附加转向角）可表示为：

联立式（2）和（16），可得直流电机的旋转角度为：

由此可得控制器输出转角与实际前轮转角输出的延迟时间为：

根据式（5）和式（17），实际转向角φs和AFS实际工作角度Δφs(t)可写为:

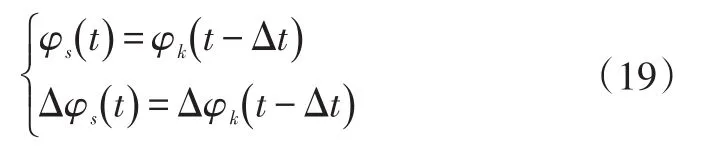
4.4 滑模控制稳定性分析

通过稳定性分析来验证滑模控制系统的稳定性。

选取李亚普诺夫Lyapunov函数:

其导数可写成:

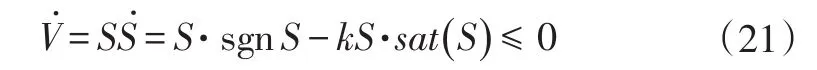
显然，除S=0外，Lyapunov函数的导数总是负值，表明以侧滑角和偏航率同时为控制变量的联合控制系统总是稳定的[6-7]。

5 仿真与试验验证

在仿真平台上，利用MATLAB和Simulink软件对SMC控制系统分别进行闭环和开环转向稳定性控制仿真试验分析，并与模糊PID策略进行比较。

以某乘用车为试验对象，设转向盘按正弦转向信号输入，评价该车转向稳定性[6,8]。设该车的主要技术参数为：汽车质量m=1 500 kg，转向装置的传动比为16.5，前轴到质心距离l1=1.280 m,后轴到质心距离l2=1.440 m,汽车绕z转动惯量Iz=1 800 g·m2，K1=49 521 N/rad，K2=60 235 N/rad，ωb=538.6 rad/s，zbr=50。

5.1 事故回避试验

设汽车以80 km/h的速度按给定路径行驶，行驶路径如图4所示。因汽车转弯时驾驶员要频繁操作转向盘，故该试验属于闭环控制。为确保行驶安全,急转弯时首先将汽车行驶到路的左侧，再慢慢返回原车道。在给定的行驶条件下，仿真结果如图5所示，两种策略下侧滑角、偏航率的峰值和均方根值对比结果如表1所列。

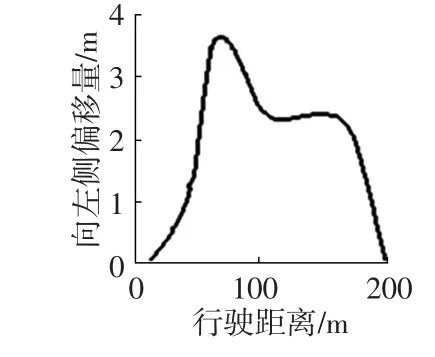
图4 汽车行驶路径

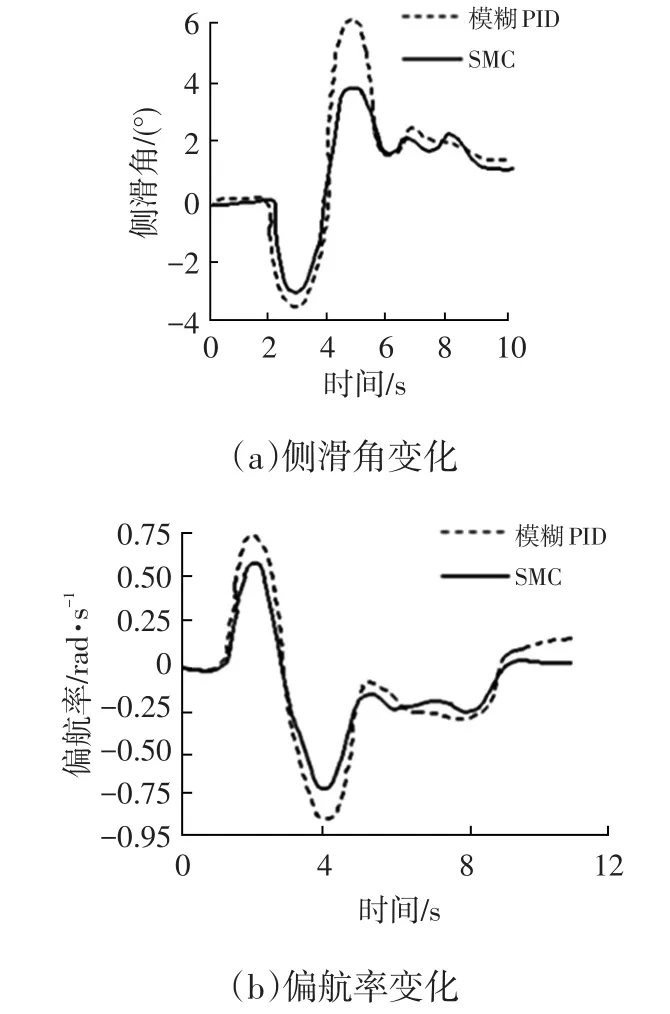
图5 事故回避仿真试验结果

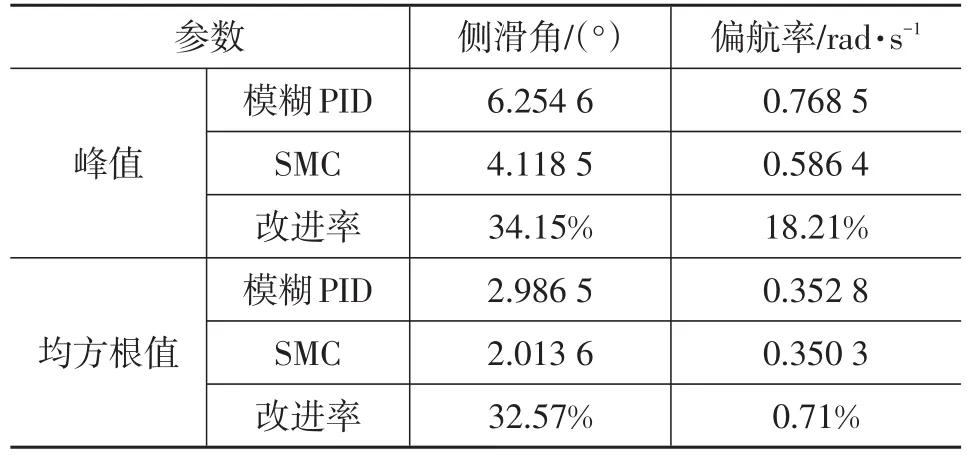
表1 两种控制策略下侧滑角、偏航率的峰值和均方根值对比结果（事故回避仿真试验）

侧滑角和偏航率值越小，表明系统稳定性越好。由图5可看出，在SMC策略下的转向稳定性比模糊PID策略下的转向稳定性要好。由表1可知，SMC策略下的侧滑角和偏航率峰值比模糊PID策略下分别降低了34.15%和18.21%，二者的均方根值分别降低了32.57%和0.71%。两参数均有不同程度的降低，表明SMC策略同时控制了两个变量，表现出更好的转向稳定性。

5.2 转向盘转角正弦输入试验

正弦输入试验时，设汽车以80 km/h的速度匀速直线行驶1.5 s后，转向盘转向模式按正弦输入，正弦波频率为0.5 Hz，最大转向角为300°，如图6所示。图7所示为仿真验证结果，表2为两种控制策略下侧滑角和偏航率的峰值、均方根值及改进率对比结果。

由图7a可看出，在模糊PID策略下，当转向盘转角由正转为负时，AFS实际工作角发生了突变，导致直流电机输出方向快速改变，将直接影响VGRS执行器的稳定性，在SMC策略下，当转向盘转角由正转为负时，AFS实际工作角变化相对平稳，表明转向稳定性较好。由图7b可看出，当汽车频繁转向后，两种控制策略下都存在不稳定性，但大多数情况下，SMC策略下的侧滑角较小，能更快地达到稳定状态。由图7c可看出，SMC策略下的偏航率呈现较稳定的变化，而模糊PID策略下的偏航率可能会失去控制。

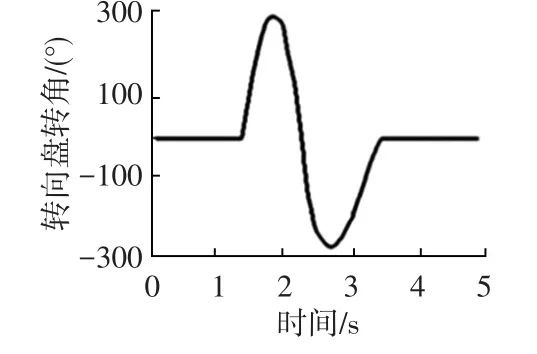
图6 转向盘转向输入模式

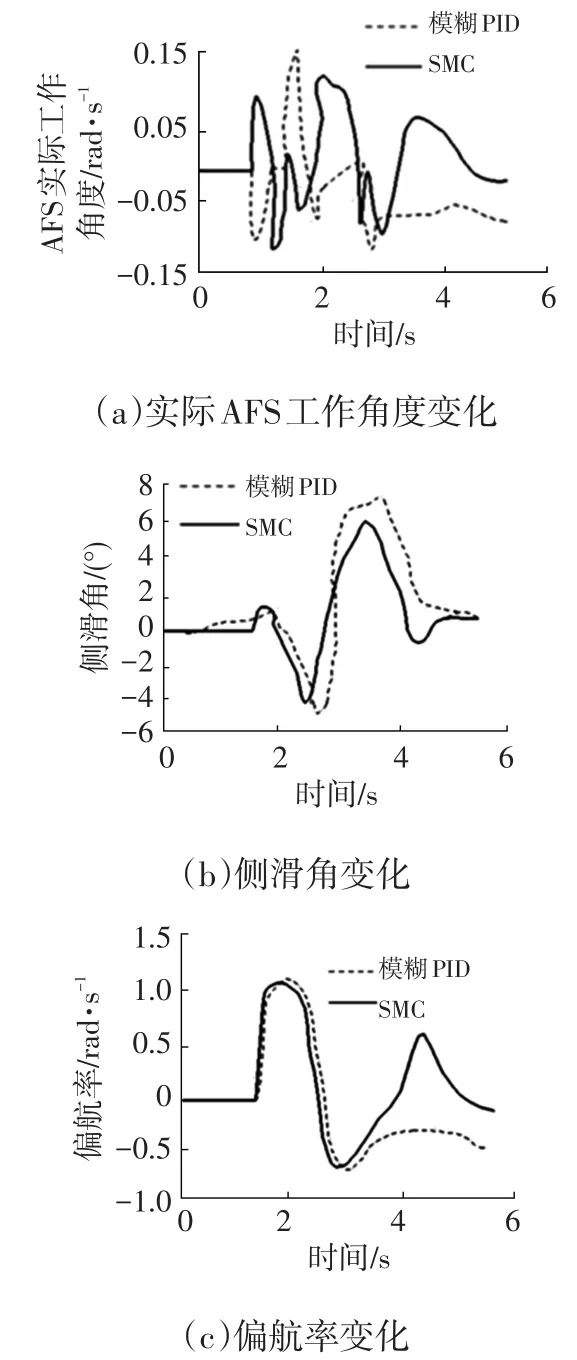
图7 仿真验证结果

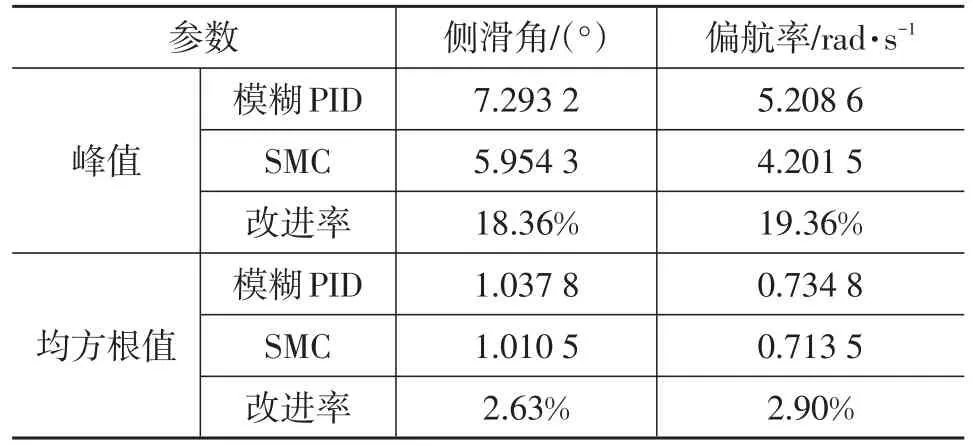
表2 两种控制策略下侧滑角和偏航率的峰值和均方根值对比结果（转向盘转角正弦输入试验）

由表2可知，与模糊PID策略相比，SMC策略下侧滑角和偏航率峰值分别低了18.36%和2.63%。SMC策略下侧滑角的均方根值下降了19.36%，偏航率的均方根值略有改善[9]。

由试验结果可知，侧滑角比偏航率改善情况较好。表明在急剧转向时，所提出的SMC策略仍能很好地控制侧滑角，但由于此时轮胎的侧向力已达到饱和，导致偏航率改善较小。

6 结束语

基于AFS系统所设计的多目标滑模控制策略，将侧滑角和偏航率两个变量作为控制目标，体现了良好的转向稳定性。由仿真验证可知，与模糊PID策略相比，SMC策略下侧滑角和偏航率均有不同程度降低，即SMC策略下的转向稳定性比模糊PID策略好。理论分析与仿真试验均表明，多目标SMC策略以侧滑角和偏航率为联合控制变量，能有效提高汽车转向稳定性，具有较强的鲁棒性。