“数形结合”巧解二次函数问题

一、原题呈现
苏科版《数学》九年级下册第25页例题:
不画图像,判断二次函数y=-x2+5x-8的图像与x轴是否有公共点.
【解析】此题考查的是对二次函数的图像与x轴公共点的认识情况,涉及由函数模型到方程模型的转化.要想判断二次函数y=ax2+bx+c的图像和x轴的公共点个数,只需将这个二次函数先转化为一元二次方程ax2+bx+c=0,再根据一元二次方程的根的情况来判断即可:(1)b2-4ac>0,一元二次方程有两个不相等的实数根,抛物线与x轴有两个公共点;(2)b2-4ac=0,一元二次方程有两个相等的实数根,抛物线与x轴有一个公共点;(3)b2-4ac<0,一元二次方程没有实数根,抛物线与x轴没有公共点.此题答案是:没有公共点.
那么除了采用“根的判别式”法判断之外,有时解方程是更加直接的方法.我们再看本页练习的第一小题:
不画图像,判断二次函数y=x2-x的图像与x轴的公共点的个数.
解法一:∵一元二次方程x2-x=0的根的判别式b2-4ac=(-1)2-4×1×0>0,
∴方程x2-x=0有两个不相等的实数根.
∴二次函数y=x2-x的图像与x轴有两个公共点.
解法二:∵一元二次方程x2-x=0的根为x1=1,x2=0,
∴二次函数y=x2-x的图像与x轴有两个公共点.
【总结】x轴其实可以看作是直线y=0,所以要想判断二次函数y=-x2+5x-8的图像与x轴是否有公共点,其实也就是判断抛物线y=-x2+5x-8和直线y=0是否有公共点,也就是的解的情况,于是得到方程-x2+5x-8=0.从解析式入手,借助方程组倒是一个可以解决二次函数的图像和直线(一次函数)的公共点问题的通法.
二、变化延伸
教材上的例题是专家们精心琢磨的数学范例,它就像一粒种子,蕴藏着巨大的能量.近几年来,二次函数的图像与x轴的公共点个数问题成为中考的热点.而将参数引入二次函数,二次函数的图像与坐标轴、直线、线段等的公共点问题是这个例题最常见的生长方向.
延伸1
例1 已知二次函数y=kx2-2x-1的图像与x轴有两个交点,则k的取值范围为_____.
例2 若二次函数y=x2+mx+4的图像如图所示,则m的值为 .

【解析】考题中经常将二次函数的图像和x轴的公共点个数作为条件,通过文字或者图像等方式给出,要求求出参数的值或者范围.
在第一题中,由二次函数的图像与x轴有两个交点,联想到一元二次方程有两个不相等的实数根,从而列出不等式b2-4ac>0,解出k的范围,另外,要注意二次项系数不可以为0;观察第二题的图像,不难发现抛物线与x轴只有一个公共点,可根据b2-4ac=0,计算出m的值,需要注意的是,此题还需要考虑二次函数图像的隐藏条件:对称轴在y轴的左侧.此题在考查知识的同时,还渗透着数形结合的数学思想.
解:1.∵二次函数y=kx2-2x-1的图像与x轴有两个交点,
∴一元二次方程kx2-2x-1=0有两个不相等的实数根,
∴b2-4ac>0,
∴(-2)2-4·k·(-1)>0,
∴k>-1,
又∵k≠0,
∴k>-1且k≠0.

∴m=4.延伸2例3 已知二次函数y=2(x-1)(x-m-3)(m为常数).
(1)求证:不论m取何值,该函数的图像与x轴总有公共点.
(2)当m取何值时,该函数的图像与y轴的交点在x轴的上方?
【解析】考题中经常出现含参的二次函数,并要求判断该函数的图像与x轴的公共点情况.这道题给出的二次函数的形式很特别,所以我们在解决问题时,既可以像往常一样,化成一般形式,从总有公共点联想到一元二次方程总有实数根,从而借助根的判别式进行判断.需要注意的是,在配方时,二次项的系数不可以直接去掉.当然,我们也可以将该二次函数转化成方程形式2(x-1)(x-m-3)=0,直接解出两个根,以根的具体形式进行讨论.
第二题主要考查了对二次函数的图像与y轴交点的认识情况,难度不大,但方法很多,既可以根据与y轴交点的横坐标特征为0,求出交点纵坐标来研究,也可以借助图像来判断m+3与0和1的大小关系,或者根据对称轴的位置求出m的范围,渗透着数形结合、分类讨论等数学思想.
证明:(1)方法一:令y=0,得2(x-1)(x-m-3)=0,
整理得:2x2-2(m+4)x+2m+6=0,
∵b2-4ac=[-2(m+4)]2-4×2(2m+6)=4m2+16m+16=4(m2+4m+4)=4(m+2)2≥ 0,
2.∵二次函数y=x2+mx+4的图像与x轴只有一个公共点,
∴一元二次方程x2+mx+4=0有两个相等的实数根,
∴b2-4ac=0,
∴m2-4×1×4=0,
∴m=4或-4,
∵对称轴在y轴左侧,
∴不论m取何值,该方程总有实数根,
∴不论m取何值,该函数的图像与x轴总有公共点.
方法二:令y=0,得2(x-1)(x-m-3)=0,
解这个方程得,x1=1,x2=m+3,
∴不论m取何值,该方程总有实数根,
∴不论m取何值,该函数的图像与x轴总有公共点.
解:(2)解法一:当x=0时,y=2m+6,
∴由2m+6>0,得m>-3,
∴m>-3时,该函数的图像与y轴的交点在x轴的上方.
解法二:2(x-1)(x-m-3)=0的两根为x1=1,x2=m+3,
若m+3<0,如下图,不符合题意,∴舍去.
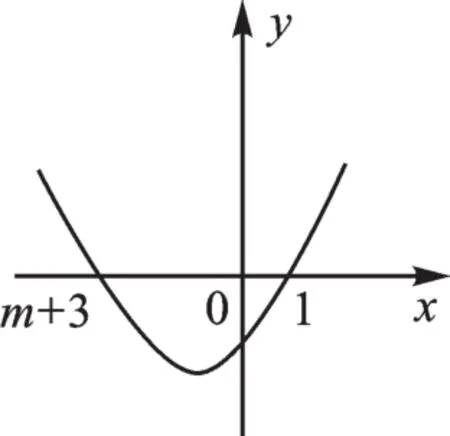
若m+3=0,如下图,不符合题意,∴舍去.

若0<m+3<1,如下图,符合题意,∴-3<m<-2.
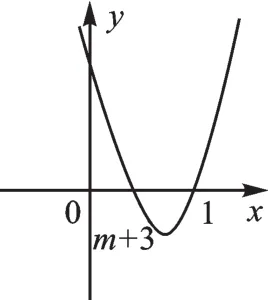
若m+3=1,如下图,符合题意,∴m=-2.
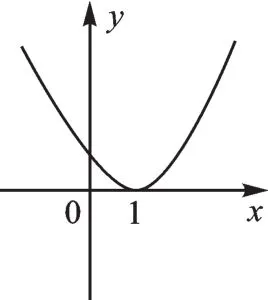
若m+3>1,如下图,符合题意,∴m>-2.
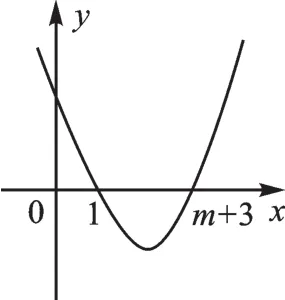
综上,m>-3.
∴m>-3时,该函数的图像与y轴的交点在x轴的上方.
解法三:2(x-1)(x-m-3)=0的两根为x1=1,x2=m+3,
∴该函数的对称轴是直线x=2+0.5m,
∵函数的图像与y轴的交点在x轴的上方,
∴2+0.5m>0.5,
∴m>-3,
∴m>-3时,该函数的图像与y轴的交点在x轴的上方.
延伸3
例4 若函数y=x2-2x+b的图像与坐标轴有3个交点,则b的取值范围是( ).
A.b<1且b≠0 B.b>1
C.0<b<1 D.b<1
【解析】根据二次函数的图像特征,它与y轴必有一个公共点.而题中y=x2-2x+b的图像与坐标轴有3个交点,也就意味着该函数图像与x轴有两个公共点,接下来可以根据二次函数所对应的一元二次方程的根的判别式Δ>0列出不等式,求出b的范围.但是,需要注意的是,当b=0时,抛物线与x轴的交点和与y轴的交点在原点处重合,不符合题中与坐标轴有3个交点的条件,故需舍去.
解:∵函数y=x2-2x+b的图像与坐标轴有3个交点,
∴函数y=x2-2x+b的图像与x轴有两个交点,
∴一元二次方程x2-2x+b=0有两个不相等的实数根,
∴Δ>0,
∴(-2)2-4×1·b>0,
∴b<1.
∵函数y=x2-2x+b的图像与坐标轴有3个交点,当b=0时,抛物线与x轴的交点和与y轴的交点在原点处重合,
∴b<1且b≠0.
故选A.
延伸4
例5 在平面直角坐标系中,直线y=4x+4与x轴,y轴分别交于点A,B,抛物线y=ax2+bx-3a经过点A,将点B向右平移5个单位长度,得到点C.
(1)求点C的坐标.
(2)求抛物线的对称轴.
(3)若抛物线与线段BC恰有一个公共点,结合函数图像,求a的取值范围.
【解析】(1)(2)略.在第三题中,由于线段BC是有范围的,且与抛物线只有一个公共点,所以通过函数图像找出不等关系,运用数形结合思想,分类讨论,即可求出a的取值范围.
解:(1)∵A(-1,0),B(0,4),∴C(5,4).
(3)∵抛物线始终经过点A(-1,0),且对称轴为直线x=1,由抛物线对称性,可知抛物线一定经过点A关于对称轴的对称点(3,0).
∴只需对a进行分类讨论即可.
①当a>0时,如下图,

把x=0代入抛物线解析式得y=-3a,把x=5代入抛物线解析式得y=12a.

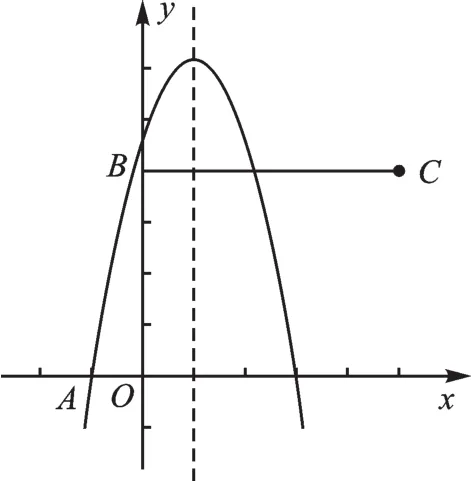

③当抛物线顶点在线段BC上时,顶点为(1,4),如下图,

把点(1,4)代入抛物线解析式,得a=-1.

总之,要解决二次函数的图像公共点问题,我们只需抓住方程、不等式、函数之间的联系,关注二次函数的“式结构”和“形结构”,留意题中的隐含条件,就可以做到一通百通.

