一节高三复习课的教学设计与备课历程

安徽省和县第一中学 (邮编：238200)

纵观目前高三复习课，以“跟着教辅走”的做法居多，市面上的高三复习资料琳琅满目，质量参差不齐.笔者也经历过“用教辅教”的阶段，课堂上学生学得枯燥、教师教得无味.高三复习是学生站在高中数学整体高度上的“二次学习”，那么，如何在复习课教学中避免“炒冷饭”式的简单回顾呢？这就需要教师重新整合知识和方法，优化教学行为，将各个教学环节高效地整合到一起，促进学生深度地参与数学学习，从而帮助学生实现内化和升华.

在近期的市级高三教研活动中，笔者上了一节家常课，课题是“正方体的那些事(第一课时)”，下面呈现该节课的教学设计以及备课历程，敬请同行专家们批评指正.

1 教学内容与学情分析

1.1 教学内容解析

本节课内容是复习数学必修2的第二章《点、直线、平面之间的位置关系》(第一课时).鉴于正方体是一个重要的空间几何模型，运用正方体可以帮助我们直观认识和理解空间中点、直线、平面之间的位置关系.所以本课以正方体为研究对象，将立体几何中的有关基础知识串联起来，组织复习教学，从课本题出发，回溯先前学生掌握的知识网络，然后以2018年一道高考题收尾，承上启下，回归定理和公理.

本节课的教学重点是：回顾复习点线面位置关系的判定与性质，计算空间角的方法.

1.2 学生学情分析

学生已经掌握了立体几何的相关公理和定理，以及空间角的计算方法.在运用这些公理和定理时，缺乏逻辑推理的严密性，缺乏对基本几何模型的研究.这些知识和能力是学生需要提高的地方.

本节课的教学难点是：让学生“看得出来，说得清楚，算得精细”，培养直观想象、逻辑推理等能力.

1.3 教学目标设置

(1)以正方体为载体，复习空间中点、直线、平面之间的位置关系；

(2)以正方体为载体，复习空间角的计算；

(3)结合正方体设计问题串，引导学生完成探究、发现、证明新问题的过程，提升直观想象、数学抽象、逻辑推理等素养，积累数学探究活动经验.

1.4 教学策略分析

(1)为了充分调动学生学习数学的积极性，促进学生主动思考，采用问题串形式引导学生探究；

(2)启发式教学始终从问题出发，层层设疑，引导学生在不断思考中获取知识；互动式教学体现在提问、例题教学、课堂练习、教师示范、学生板演、课堂小结等方面，引导学生积极参与.

(3)关注教学内容与现代教育手段的合理整合，利用几何软件展现动态过程，通过多媒体(几何软件、PPT等)和板书相结合来提高课堂效益；

本节课的教学手段是：多媒体和板书相结合，师生共同探讨.

2 教学过程设计

正方体是一个重要的空间几何模型.运用正方体，可以帮助我们直观认识和理解空间中点、直线、平面之间的位置关系；利用正方体，专家学者们命制了一批优秀的试题，课本里有，高考题里有，竞赛题里也有.今天，让我们一起重温经典，开启正方体的探究之旅.

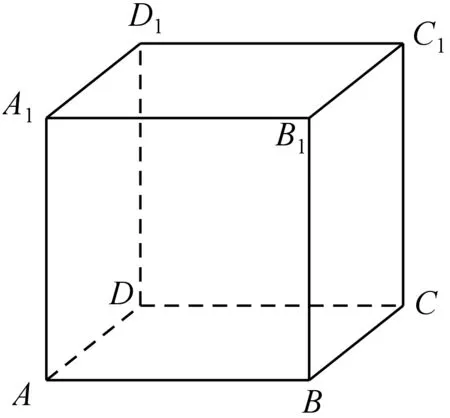
图1

环节一自主命题

同学们，如果给你一个正方体(如图1)，你能命制一道立体几何问题吗？

设计意图打造开放的课堂教学，从学生们最熟悉的正方体入手，放手让学生自己编题，问题开放，调动学生的已有知识储备以及学习积极性.培养学生“提出问题、发现问题”的能力，同时也是调查学生们对正方体的认知程度.

环节二课本里的正方体(温故与知新)

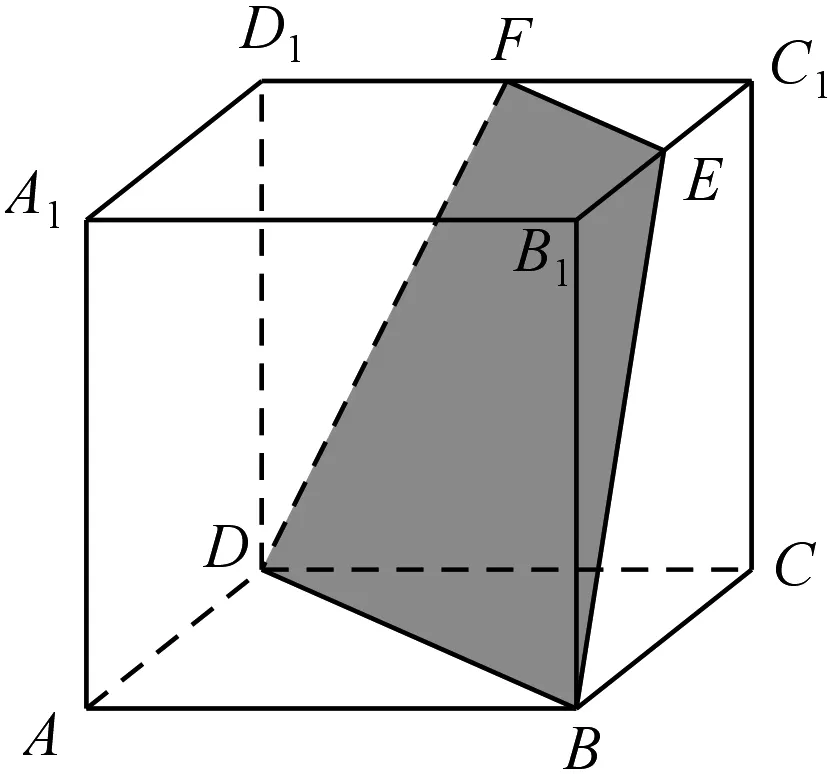
图2

例1 (人教A版数学必修2第78页A组第4题)如图2，正方体ABCD-A1B1C1D1的棱长是a，点E、F分别是两条棱的中点.

问题1 证明：DF、BE、CC1三条直线相交于同一点；

问题2 证明：四边形DBEF是一个梯形；

问题3 求四边形DBEF的面积.

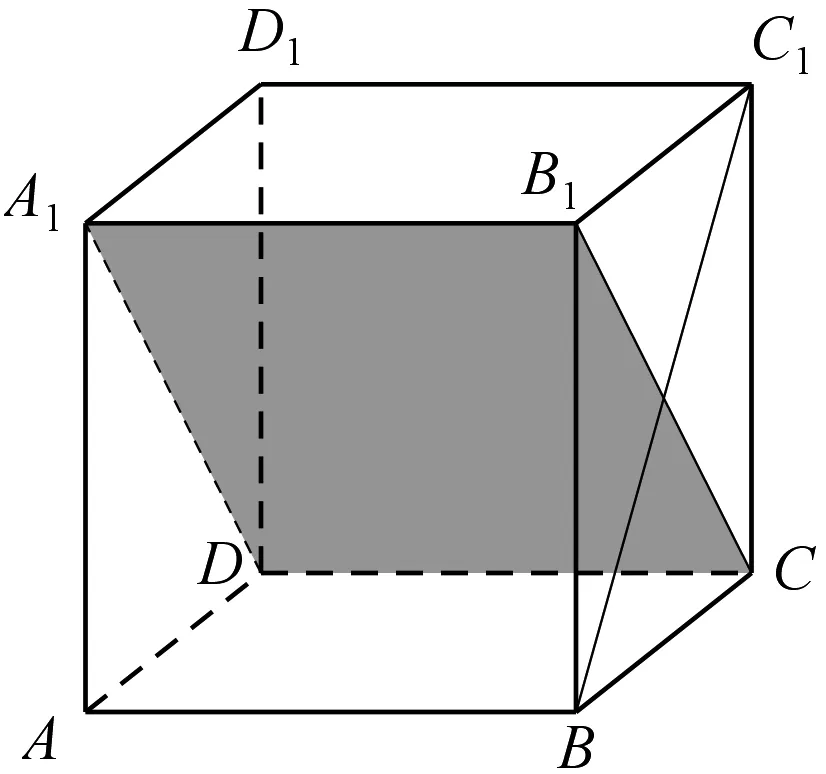
图3

例2 (人教A版数学必修2第66页例2)如图3，在正方体ABCD-A1B1C1D1中.

问题1 证明：BC1⊥平面A1B1CD；

问题2 求直线A1B和平面A1B1CD所成的角；

问题3 求平面A1B1CD与正方体的各个面所成二面角的大小分别是多少？

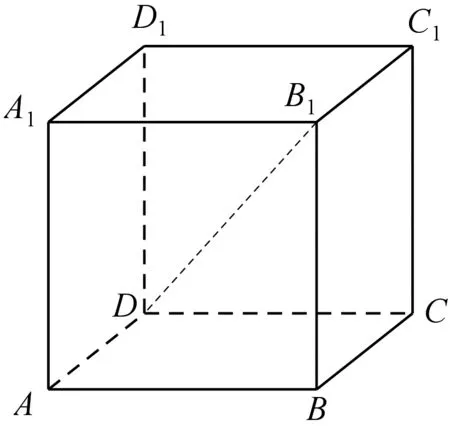
图4

例3 (人教A版数学必修2第79页B组第2题)如图4，在正方体ABCD-A1B1C1D1中.

问题1 求直线B1D与直线AB所成角的余弦值；

问题2 求直线B1D与正方体每条棱所在的直线所成角的余弦值；

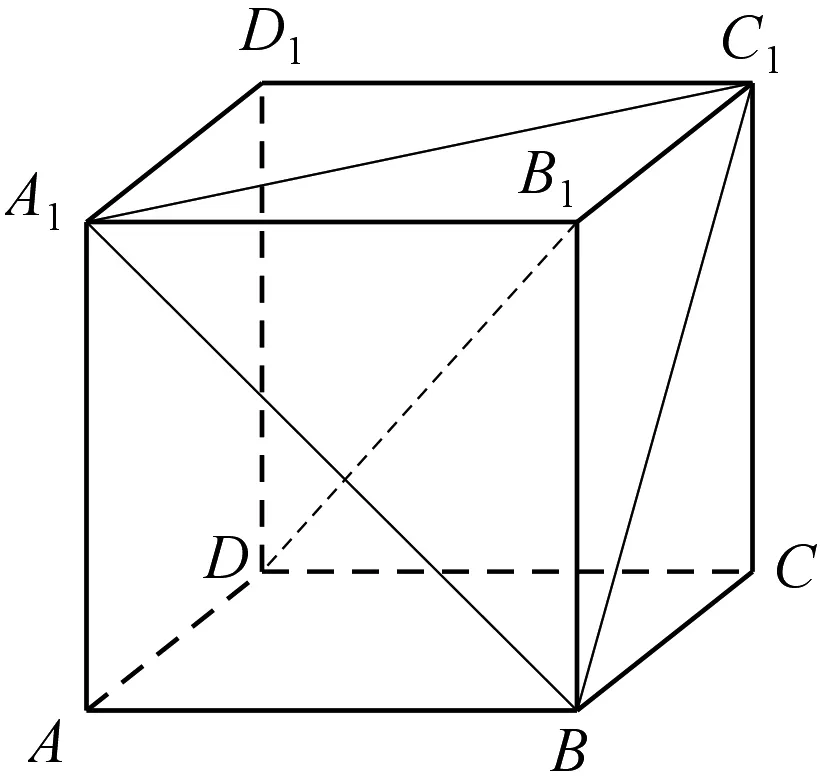
图5

问题3 求直线B1D与直线BC1所成角的余弦值；

问题4 求直线B1D与正方体每个面对角线所在的直线所成角的余弦值；

问题5 证明：B1D⊥平面A1C1B；

问题6 求直线A1B1与平面A1C1B所成角的余弦值；

问题7 证明：正方体每条棱所在直线与平面A1C1B所成的角都相等.

设计意图结合课本题，设计该组问题串，教学时引导学生逐步探究，可以针对不同的学生，设计不同的教学方式，通过多种方法实施探究.适当时候可以提出以下三个探究问题.

探究1 给定空间中的两条直线l1、l2，求作一个平面α，使得直线l1、l2与平面α所成的角相等.

探究2 给定空间中的三条直线，求作一个平面α，使得这三条直线与平面α所成的角都相等.

探究3 求作一个平面α，使得正方体每条棱所在直线与平面α所成的角都相等.

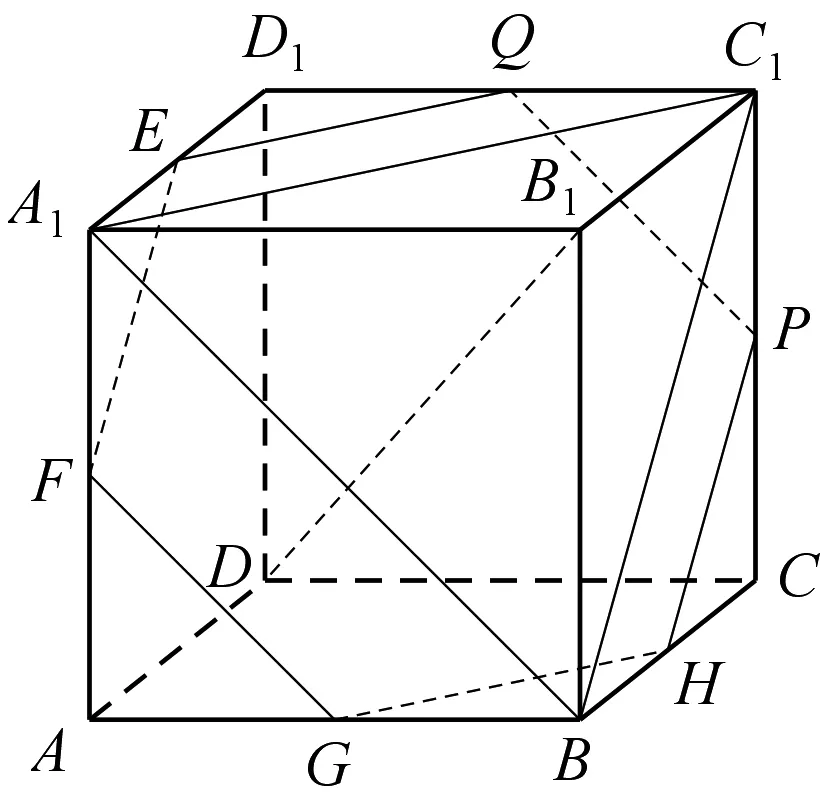
图6

例4 (人教A版数学选修2-1第112页A组第4题)如图，在正方体ABCD-A1B1C1D1中.

问题1 如图6，若点E、F、G、H、P、Q分别是A1D1、AA1、AB、BC、CC1、C1D1各棱的中点，

(1)求证：平面A1C1B∥平面EFGHPQ；

(2)求证：B1D⊥平面EFGHPQ.

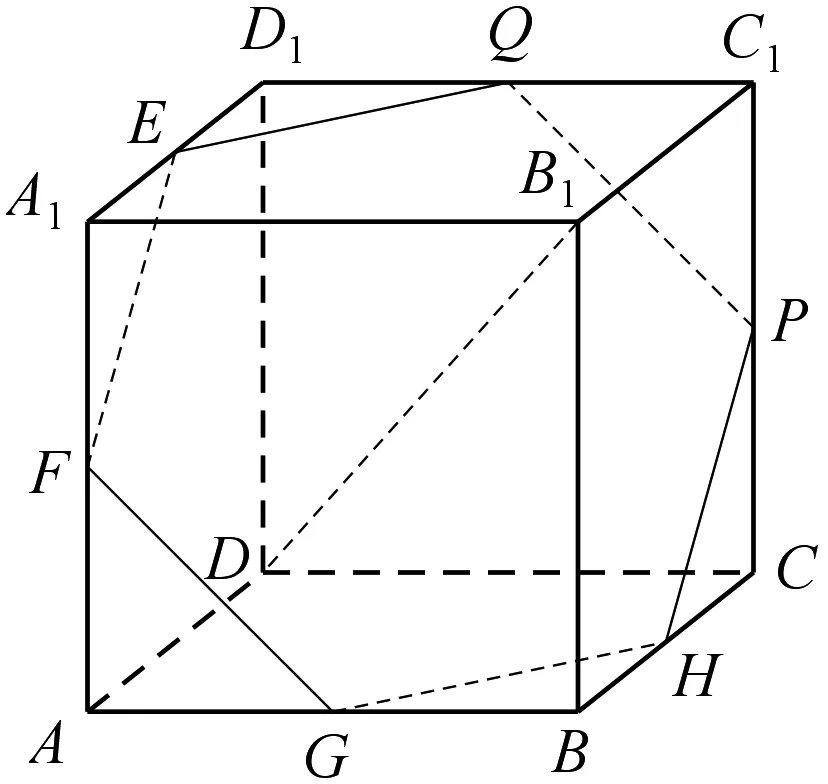
图7

问题2 如图7，任作平面α与对角线B1D垂直，使得α与正方体的每个面都有公共点，记这样得到的截面多边形为EFGHPQ.

(1)求证：EQ∥GH∥A1C1；

(2)设A1E=x，请用x来表示截面多边形EFGHPQ的面积和周长.

设计意图精选了课本里的4道例题和习题，并在设问上作了一些改编.带领学生共同回顾基本模型中的常见位置关系，熟悉这些位置关系对解题会有很大的帮助.4道题所涉及到的知识点包括点、直线、平面之间的位置关系，以及空间角(异面直线所成角、线面角、二面角)的计算.回归课本，激活教材，挖掘教材的深刻内涵，一题多问，采用问题串形式引导学生自主探究.

环节三高考里的正方体(立足与拔高)

例5 (2017年高考数学全国3卷文科第10题)在正方体ABCD-A1B1C1D1中，E为棱CD的中点，则( )

A．A1E⊥DC1B．A1E⊥BD

C．A1E⊥BC1D．A1E⊥AC

例6 (2017年高考数学全国1卷文科第6题)如图8，在下列四个正方体中，A、B为正方体的两个顶点，M、N、Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是( )

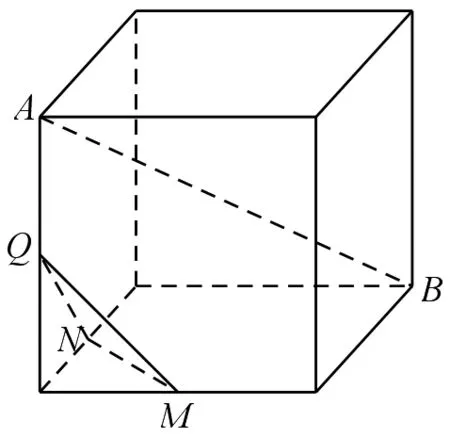
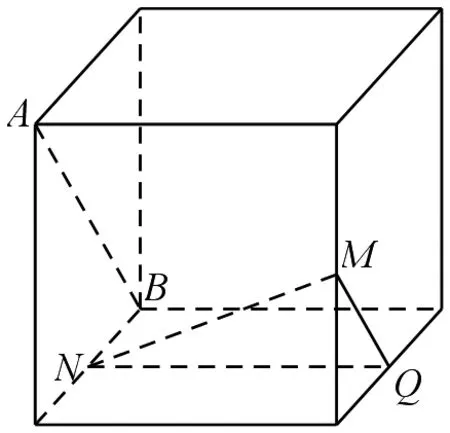
图8

例7 (2016年高考数学全国1卷第11题)平面α过正方体ABCD-A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD=m，α∩平面ABB1A1=n，则m、n所成角的正弦值为( )

The corresponding time dependence of the experimental resistance modulation index is that given in Fig. 1 (Bottom)after scaling M by the divisor Ro.

例8 (2018年高考数学全国1卷第12题)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为( )

设计意图精选了近3年高考数学全国卷里的4道试题，带领学生共同赏析高考题中的正方体.有了前面课本4道题的探究基础，解决这4道高考题并不困难，让学生感受到高考题就是源于课本.

环节四竞赛里的正方体(回望与启迪)

例9 (1994年全国高中数学联赛第11题)已知一平面与一正方体的12条棱的夹角都等于α，则sinα=___________.

例10 (2005年全国高中数学联赛第4题)已知ABCD-A′B′C′D′为正方体. 任作平面α与对角线AC′垂直，使得α与正方体的每个面都有公共点，记这样得到的截面多边形的面积为S，周长为l，则( )

A．S为定值，l不为定值

B．S不为定值，l为定值

C．S与l均为定值

D．S与l均不为定值

设计意图针对2018年高考数学全国1卷第12题，追根溯源，其实就是两道竞赛题的简单组装，让学生领悟命题的技术.

环节五课堂小结

本节课通过研究正方体，重点复习了空间中点、直线、平面之间的位置关系，以及空间角(异面直线所成角、线面角、二面角)的计算.只要同学们深入研究课本题的知识和方法，高考题不再神秘，竞赛题也不再高不可攀.

未完待续，有关正方体的故事还有很多.比如，三视图还原几何体时经常用到正方体载体，将正四面体放入正方体中去研究等.下节课我们将继续探究有关正方体截面的问题(布置学生课后探究，截面的形状会是什么样的？)，还有正方体中面积与体积以及距离的计算.

设计意图理清知识和方法结构，展现本节课的教学立意——每节复习课都应引导学生学会思考、学会研究.

3 梳理备课历程

众所周知，备课对课堂教学具有定向作用，备好课是上好课的一个必要条件.备课的结果往往是以一份教学设计呈现出来，在“互联网+”时代，教师获取一份甚至质量较高的教学设计都不是一件难事，困惑的是拿着这样一份优秀教案未必能演绎一节精彩的课.究其原因，就是呈现出来的教学设计已经扫除了备课时的痕迹，没有亲自经历“深入”的备课，很难做到“浅出”.在平时与同行的交谈中还发现，有些教师在备课时确实花了很多时间和精力，可备出的课还是不尽如人意.因此，加强备课研究，已经成为提高教学质量和效益的根本措施之一.高三复习备课因其特殊性，与高一高二又有所区别，需要进一步把高中数学内容串连起来理解，加以融会贯通，从而实现知识理解的“由厚到薄”.

本课的备课经历了选定对象、广泛涉猎、搭建框架、精细装修四个阶段，每个阶段都是一次自我的提升.

3.1 选定对象

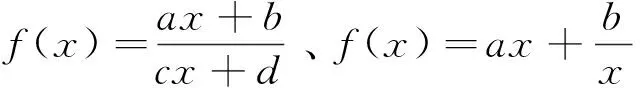
3.2 广泛涉猎

首先认真学习课程标准以及考试大纲对该专题内容的具体要求，然后收集整理研究对象“正方体”的课本题、历年高考真题以及优秀模拟试题甚至竞赛题等，做到教师先下题海.一旦收集到的素养越丰富，后面的教学设计就越精彩.

3.3 搭建框架

针对该专题内容，从构成要素以及思想立意两方面设计框架结构.根据我校学情分析，本课最终确定了“五个环节”的整体框架，主体的“三个环节”分别通过“课本里的正方体”来“温故知新”“高考里的正方体”来“立足拔高”“竞赛里的正方体”来“回望启迪”.对学生已有的知识网络结构进行整体的优化设计，做到探中抽知，串知成链，动态生成.

3.4 精细装修

本课例中所选用的课本题都做了相应的改编，尽可能做到一题多问，层层设疑，引导学生在不断思考中获取知识.

波利亚曾经指出：“良好的组织使得所提供的知识容易用上，这甚至可能比知识的广泛更为重要.”依托主题明确、针对性极强的“微专题”进行复习，可以促进学生的深度学习，从而有利于学生获得清晰的数学知识网络、系统的数学研究方法，加深对数学的理解，提高自身的数学素养.