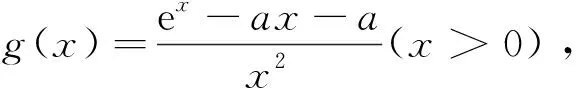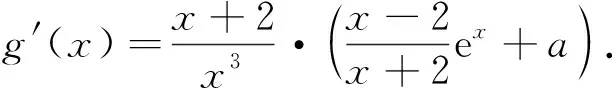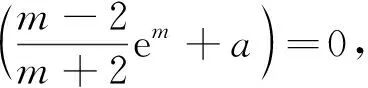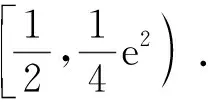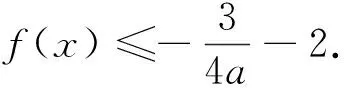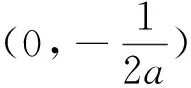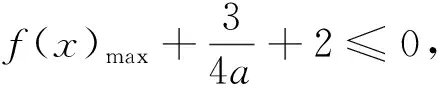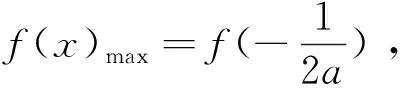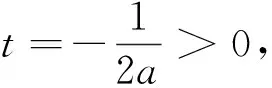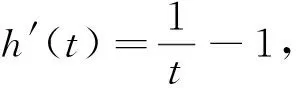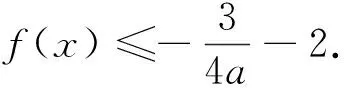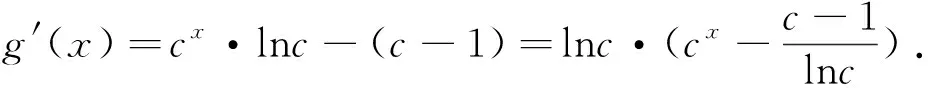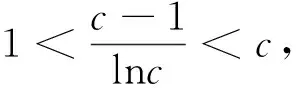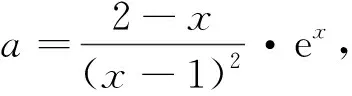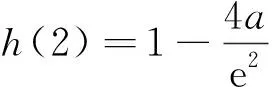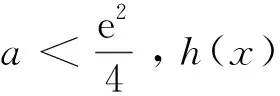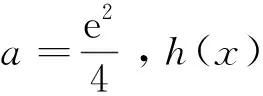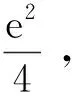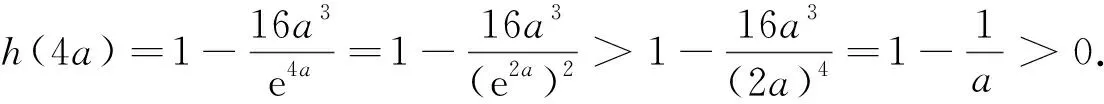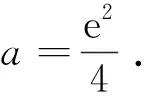例谈构造辅助函数破解高考压轴题的方法

陕西省汉中市镇巴县镇巴中学 (邮编：723600)

查阅近十年全国卷高考数学34道压轴题，除文科2013年全国卷一和2016年全国卷二压轴题以圆锥曲线为基础命制外，其余32道压轴题都是以函数与导数为核心命制的函数综合问题，这32道函数综合压轴题中有20道需要构造辅助函数才能顺利解决，构造辅助函数对学生的创造性与创新性思维能力的要求较高，那么辅助函数的构造有规律可循吗？构造辅助函数解决压轴题的具体方法有哪些呢？本文立足于此，并以近几年高考压轴真题为例进行阐述，希望对广大高三学生的复习备考有所帮助.

方法一观察分析构造

观察是科学研究的重要方法，也是数学解题的首要心理活动，更是构造辅助函数最为直接的策略.

例1 (2016年全国卷1理科压轴题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)设x1、x2是f(x)的两个零点，证明：x1+x2<2.

解(1)a的取值范围为(0,+∞) ;

(2)求导得f′(x)=(x-1)(ex+2a)，由(1)知a>0.

所以函数f(x)的极小值点为x=1，结合要证结论x1+x2<2，即证x2<2-x1,考虑到若2-x1和x2属于某一个单调区间的话，那么只需要比较f(2-x1)和f(x2)的大小，即探求f(2-x)-f(x)的正负性，于是通过上述观察分析，即可构造辅助函数F(x)=f(2-x)-f(x),x<1，代入整理得F(x)=-xe-x+2-(x-2)ex求导得F′(x)=(1-x)(ex-e-x+2)，即x<1时，F′(x)<0，则函数F(x)是(-∞,1)上的单调减函数，于是F(x)>F(1)=0，则f(2-x)-f(x)>0，即f(2-x)>f(x).

因为x1、x2是f(x)的两个零点，并且在x=1的两侧，所以不妨设x1<1

故x1+x2<2，得证.

点评此题的压轴问以函数零点为依托，看似证明不等式，实则是极值右偏问题，解决的核心是通过观察分析构造辅助函数F(x)=f(2-x)-f(x)，建立抽象不等式“f(x2)

方法二整体构造

整体思想是从问题的整体性质出发，突出对问题的整体结构的分析和改造，发现问题的整体结构特征，把某些式子或图形看成一个整体，进行有目的、有意识的整体处理. 整理构造辅助函数就是立足这一思想来解决函数综合题的一种策略.

例2 (2017年全国卷2理科压轴题)已知函数f(x)=ax2-ax-xlnx，且f(x)≥0.

(1)求a；

(2)证明：f(x)存在唯一的极大值点x0，且e-2

解(1)a=1;

(2)由(1)f(x)=x2-x-xlnx，求导得f′(x)=2x-2-lnx.

又因为x=x0是f(x)在(0,1)的最大值点，结合e-1∈(0,1),f′(e-1)≠0,得f(x0)>f(e-1)=e-2.

所以e-2

方法三局部构造

若问题的整体结构比较复杂，使得正面解决很困难时，可以考虑将复杂的整体看成几个部分，实施局部构造辅助函数，从局部突破，从而达到解决问题的目的.

解(1)略；

所以函数g(x)在(0,m)上单调递减，在(m,+∞)上单调递增，于是x=m为函数g(x)的极小值点，也为最小值点，即当a∈[0,1)时，函数g(x)有最小值g(m).

所以当a∈[0,1)时，有m∈(0,2]，于是函数g(x)的最小值，

点评此道压轴题g(x)的导函数结构比较复杂，于是我们从局部实施突破，构造辅助函数. 这种构造方式比较常见，如2016年江苏卷19题，2013年陕西卷理科压轴题等.

方法四多次构造

有时第一次构造辅助函数并不能达到问题的解决，还需要第二次甚至更多次的构造才能解决问题.

例4 (2017年全国卷3文科压轴题)已知函数f(x)=lnx+ax2+(2a+1)x.

(1)讨论f(x)的单调性；

当a≥0时，f′(x)≥0，则f(x)在(0,+∞)内单调递增；

所以h(t)在(0,1)内单调递增，在(1,+∞)内单调递减，则h(t)max=h(1)=0.

方法五和差构造

和差法常用于比较大小、构造对偶式等，其实也可用来构造辅助函数.

例5 (2016年全国卷3文科压轴题)设函数f(x)=lnx-x+1.

(1)讨论f(x)的单调性；

(3)设c>1，证明：当x∈(0,1)时，1+(c-1)x>cx.

解(1)、(2)略.

(3)作差构造辅助函数g(x)=cx-(c-1)x-1，x∈[0,1]，要证原不等式，即证g(x)<0.

所以g′(0)<0且g′(1)>0，结合g′(x)是单调递增函数和零点定理可知g′(x)在区间(0,1)上有唯一零点.

所以函数g(x)在区间(0,1)上先单调递减，再单调递增，又g(0)=g(1)=0，从而在区间(0,1)上g(x)<0，故原不等式得证.

点评和差构造辅助函数的方法在每年高考压轴题中运用广泛，如2016年四川理科压轴题、2013年辽宁理科压轴题等.

方法六变参分离构造

若条件中含有参数，要探究参数的取值范围，此时可以考虑将参数与其他变量分离，然后构造辅助函数求解参数的取值范围.

例6 (2016年全国卷1理科压轴题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)略.

解(1)显然x=1不是函数f(x)的零点.

所以函数g(x)在(-∞,1)上单调递增，在(1,+∞)上单调递减.

因为函数g(x)在(-∞,1)上的取值范围是(0,+∞)，而在在(1,+∞)上取值范围是(-∞,+∞).

所以当a>0时，函数f(x)有两个零点，故a的取值范围为(0,+∞).

点评此题将主元与参数变参分离后构造辅助函数，再对辅助函数求导探究单调性或最值，参数的范围便自然得到.

方法七常数分离

例7 (2018年全国卷二理科压轴题)已知函数f(x)=ex-ax2.

(1)若a=1，证明：当x≥0时，f(x)≥1；

(2)若f(x)在(0,+∞)内只有一个零点，求a的值.

解(1)略.(2)函数f(x)=ex-ax2两边同时乘以设函数e-x，即e-xf(x)=e-x(ex-ax2)=1-ax2e-x，目的是把变量中的常数1分离出来，由于e-x>0，所以f(x)在(0,+∞)内只有一个零点当且仅当h(x)在(0,+∞)只有一个零点，于是构造辅助函数h(x)=1-ax2e-x.

当a≤0时，h(x)>0，h(x)没有零点；

当a>0时，h′(x)=ax(x-2)e-x.

当x∈(0,2)时，h′(x)<0；当x∈(2,+∞)时，h′(x)>0，所以h(x)在(0,2)内单调递减，在(2,+∞)内单调递增.

故h(x)在(2,4a)内有一个零点，因此h(x)在(0,+∞)内有两个零点.

掌握数学就意味着必须要善于解题，中学数学教学的首要任务之一就是要加强解题训练.而人的高明之处在于当他碰到一个不能直接克服的障碍时，他就会绕过去，当原来的问题看起来似乎不好解时，就会想出一个合适的辅助问题去解决原问题，这种方法正是解决高考函数综合问题的良策与通法.通过构造辅助函数统一地处理这些问题时，其实我们已经站在了更高的层面，不再仅仅追求千奇百怪“诡异”的解法，而是理解了这些多题的共性，在统一解决的同时，给人一种思维清晰、神清气爽的良好数学感觉.