剖析空间几何体中的数学文化题

■山东省肥城市第一高级中学

空间几何体中的数学文化题,追根溯源就是化归为求“几何体的面积或体积、三视图还原几何体、分割法或补形法求非规则体的体积、模型或直接法求解球的体积,以及两种思维方法探究新定义和存在性问题”,凸显“空间问题的模型化、代数化和几何化”的本质属性。

一、借助几何体体积的计算构建方程求值

例1 (2018年安徽黄山高三一模)《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺。问积几何。答曰:二千一百一十二尺。术曰:周自相乘,以高乘之,十二而一”。这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”。就是说:圆堡瑽(圆柱体)的体积(底面圆的周长的平方×高)。则由此可推得圆周率π的取值为( )。

注:1丈=10尺。

A.3 B.3.14 C.3.2 D.3.3

解析：设圆柱体的底面半径为r,高为h,由圆柱的体积公式得V=πr2h。

溯源直接求解柱体、锥体、台体的体积,本题在阅读理解的基础上借助圆柱体积的两种计算方法,利用同一个圆柱其体积相等构建方程求解圆周率π,凸显“收集、处理、应用信息和公式”探索求解问题的能力。

二、由三视图求几何体的面积

例2 (2018年厦门模拟)《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图1所示,俯视图中的虚线平分矩形的面积,则该“堑堵”的侧面积为( )。

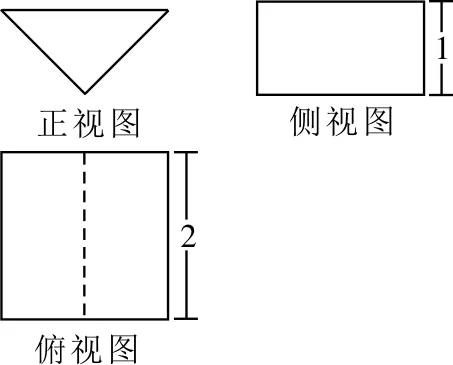
图1

解析：该几何体是一个放倒的直三棱柱ABC-AˊBˊCˊ,底面是一个直角三角形,两条直角边分别是2,斜边是2,且侧棱与底面垂直,侧棱长是2,所以几何体的侧面积S=2×2+2×2× 2=4+42,故选C。

溯源：反馈“堑堵”的意义,由三视图还原几何体求面积,实质是求一个倒放的底面为等腰直角三角形的直三棱柱的侧面积,凸显“信息迁移和空间想象”的数学素养。

三、构造球的模型求解体积计算

例3 《九章算术》是我国古代著名数学经典。其中对勾股定理的论述比西方早1000多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小。以锯锯之,深一寸,锯道长一尺。问径几何。”其意为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺。问:这块圆柱形木料的直径是多少?”长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图2所示(阴影部分为镶嵌在墙体内的部分)。已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( )。

图2

A.600立方寸 B.610立方寸

C.620立方寸 D.633立方寸

解析：如图3,依题设知AB=10(寸),则 AD=5(寸),CD=1(寸)。

设圆O的半径为x(寸),则OD=(x-1)(寸)。

在Rt△ADO中,由勾股定理可得52+(x-1)2=x2,解得x=13(寸)。

图3

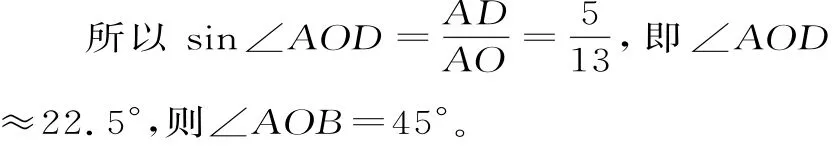
溯源：根据平面图形将问题转化为圆的几何性质,本题实质为由弦长和弓形的高求弓形面积,涉及弦长、弦心距和半径构成直角三角形三边的应用以及弧长、圆心角的弧度数、扇形面积和三角形面积的计算,凸显“空间问题模型化和平面化”的本质属性。

四、构造长方体的外接球求面积的最小值

例4 鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称。从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图4,若正四棱柱体的高为4,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为____。(容器壁的厚度忽略不计)

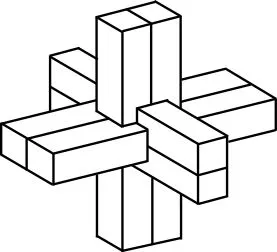
图4

解析：注意十字立方体,其上下、左右、前后完全对称的特征,构建长方体的模型,表面积最小的球形容器可以看成长、宽、高分别为1、2、6的长方体的外接球。设球的半径为R,则4R2=12+22+32=41,所以该球形容器的表面积的最小值为4πR2=41π。

溯源：能容纳十字立方体的表面积最小的球实质为构建的长方体的外接球,利用体对角线的长为外接球的直径,利用球的表面积公式求解,凸显“运动变化观念和构造模型求解最值”的思维方法。

五、构建函数模型求解最值问题

例5 中国古代名词“刍童”原来是草堆的意思,古代用它作为长方棱台(上、下底面均为矩形的棱台)的专用术语。关于“刍童”体积计算的描述,《九章算术》注曰:“倍上袤,下袤从之。亦倍下袤,上袤从之,各以其广乘之,皆六而一。”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘；将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘。把这两个数值相加,与高相乘,再取其六分之一。以此算法,现有上下底面为相似矩形的“刍童”,相似比为,高为3,且上底面的周长为6,则该“刍童”的体积的最大值是( )。

溯源：本题中的“刍童”是底面为矩形的四棱台,由一个矩形的周长、相似比及高为定值,按照给出的公式构建目标函数求其最大值,引入底面边长为变量,利用给出的公式构建目标函数,借助二次函数求最值,凸显“空间问题模型化和代数化”的简捷途径。