立体几何中探究性问题的追根溯源

■河南省商丘市第一高级中学

高考中的立体几何探索性试题我们一般可以采用综合推理的方法、分析法、特殊化法和向量法来解决。

探索性问题主要是对平行、垂直关系的探究,这类试题的一般设问方式是“是否存在?存在给出证明,不存在说明理由”。解决这类试题,一般根据探索性问题的设问,首先假设其存在,然后在这个假设下进行推理论证,如果通过推理得到了合乎情理的结论就肯定假设,如果得到了矛盾就否定假设。

例题如图1,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=2a,点E在PD上,且PE∶ED=2∶1。

(1)证明PA⊥平面ABCD。

(2)求以AC为棱,EAC与DAC为面的二面角的大小。

(3)问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论。

解析：(1)因为底面ABCD是菱形,∠ABC=60°,所以AB=AD=AC=a,在△PAB中,由PA2+AB2=2a2=PB2,知PA⊥AB,同理PA⊥AD,所以PA⊥平面ABCD。

图1

(2)作EG∥PA交AD于G,由PA⊥平面ABCD,知EG⊥平面ABCD,作GH⊥AC于H,连接EH,则EH⊥AC,则∠EHG为所求二面角的平面角,设为θ。又PE∶以θ=30°。

(3)以A为坐标原点,直线AD,AP分别为y轴,z轴,过A点垂直平面PAD的直线为x轴,建立空间直角坐标系,如图2所示。由题设条件,相关各点的坐标分别为A(0,0,0),

图2

解题思路：(1)证明的是线面垂直,只要努力去找直线与平面内的两条相交直线垂直即可；(2)按找二面角的方法进行；(3)通过建立恰当的直角坐标系,给出相应点的坐标,利用坐标关系和向量的相等就可以解决了。

例题追根溯源：如图1,在底面是菱形的四棱锥P-ABCD 中,∠ABC=60°,PA=AC=a,PB=PD=2a,点E在PD上,且PE∶ED=λ∶1(λ∈N*)。

(1)证明PA⊥平面ABCD。

(2)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论。

解析：(1)因为底面ABCD是菱形,∠ABC=60°,所以AB=AD=AC=a,在△PAB中,由PA2+AB2=2a2=PB2,知PA⊥AB,同理PA⊥AD,所以PA⊥平面ABCD。

(2)解法一:以A为坐标原点,直线AD,AP分别为y轴,z轴,过A点垂直平面PAD的直线为x轴,建立空间直角坐标系,由题设条件,相关各点的坐标分别

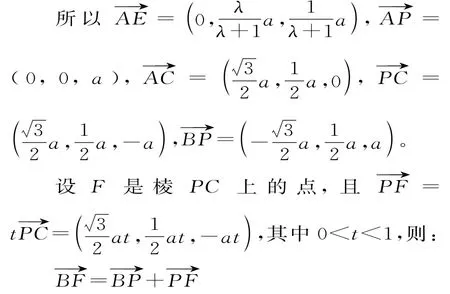
审题方法：F是段线PC上的点,一般可,求出t的值,点P是已知的,即可求出点F。

解题思路：通过建立恰当的直角坐标系,给出相应点的坐标,令所求直线对应的向量用该平面内的两个不共线向量表示即可。

解法二:如图3,在PE上取一点M,使得ME=ED,过 点M 作MF∥EC交PC于点F,连接BD交AC于点O,连接EO,BM。

图3

在△DBM中,E,O分别是DM,DB的中点,所以EO∥BM,即BM∥平面AEC。

审题方法：作出适当的辅助线,利用中位线定理找到平行关系。

解题思路：从E点出发,在线段PE上找到点M,使得E成为MD的中点,连接OE,构造△DBM的中位线,下面只需作MF∥EC交PC于点F,这样点F就被找到了。