我国建筑业投入、产出与社会经济增长关系实证研究

王 鑫

安徽理工大学经济与管理学院,淮南，232001

1 相关研究

近年来，建筑业对国家经济发展的影响越来越大。2014年，全国建筑企业的建筑业总产值为176 713.40亿元;完成竣工产值100 719.51亿元;房屋施工面积达到125.02亿m2，比上一年增长10.4%;房屋竣工面积达到42.31亿m2，比上一年增长5.4%;实现利润6 913亿元，比上一年增长13.7%。建筑业是我国重要的经济支柱产业之一，但在我国经济进入新形势下，建筑业也面临了新的挑战,同时建筑业对其他诸如钢铁、冶金等行业也有很强的拉动作用，因此,分析建筑业增长原因，有利于进一步推动经济增长。高婷婷运用改进的C-D生产函数和Granger因果检验研究了河南省建筑业经济增长原因，认为技术进步对河南建筑业的影响较低，建筑业处于粗放增长阶段[1]；而王川等人在分析中减少了变量个数并运用协整理论，对建筑业投资与经济增长的关系进行了分析，认为两者间是存在双向的因果关系[2]；韩冰从建筑业产出与经济增长关系角度比较分析了我国西部、中部和东部地区的状况，得出的结论是建筑业对经济增长与地区经济发展程度呈反比[3]。杨锦运用因子分析和数据包络分析从建筑业资本投入、建筑业劳动投入、技术进步和建筑业产出四个方面对陕西省建筑业增长的情况进行综合评价，并且指出其发展方向[4]。本文利用协整理论、误差修正模型[5]和Granger因果检验理论[6]，探究建筑业投入、产出与经济发展三者的动态关系，借助Eviews 8.0对1991—2014年的相关事件序列进行实证分析[7]。

2 研究指标与样本选取

选取1991—2014年《中国统计年鉴》相关数据[8]，对原始数据取对数以消除异方差的影响。建筑业投入用建筑业固定资产投资(jtz)表示，建筑业产出用建筑业总产值(jz)表示，经济增长用国内生产总值(GDP)表示[9]。

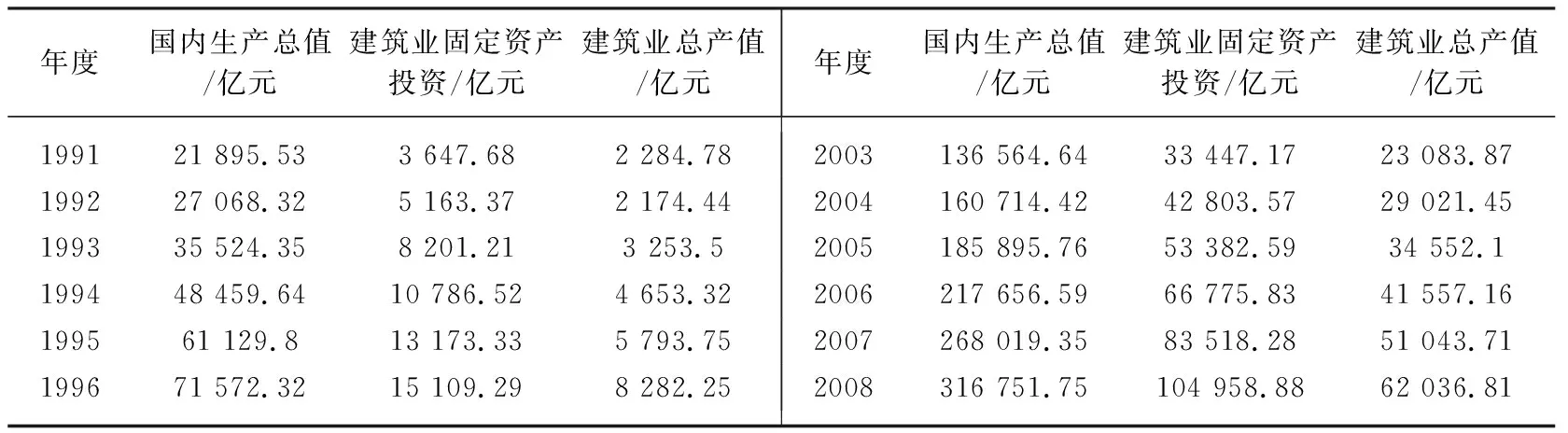
表1 1991—2014年建筑业投入、产出与GDP原始数据

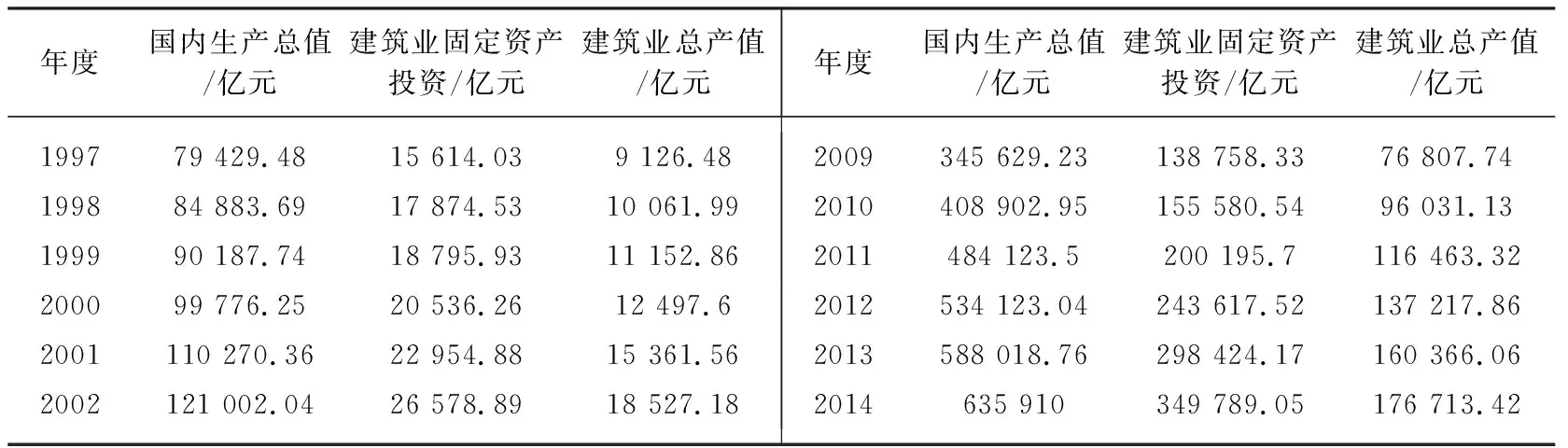
(续表1)

3 实证研究

3.1 单位根检验(ADF)序列平稳性

对于平稳序列可直接建模分析，对于非平稳序列，则必须进行差分处理或使用协整分析。对于一个平稳的时间序列，若其均值与时间无关并且序列数值围绕均值上下平稳波动，具有比较显著的收敛趋势，这样的序列就称为零阶单整，记为I(0)；若原始序列不平稳，但一阶差分平稳，则称原始序列一阶单整，记为I(1)。以此类推，如果P次差分后平稳，原始序列为P阶单整，记为I(P)。误差修正模型(VEC)中各变量一般要满足一阶或二阶单整，以利于后续的Johansen协整检验和Granger因果关系检验。单位根检验(ADF)是比较通用的序列平稳性检验方法。本文运用这单位根检验法对lnGDP,lnjz,lnjtz进行平稳性检验，结果如表2所示。

表2 单位根检验结果

注：(1)c,t,k分别表示截距、趋势和滞后阶数，滞后阶数依据AIC和SC准则进行选取；(2)D表示一阶差分。

三个变量表现为一阶单整，即其一阶差分平稳，记为lnGDP-I(1)，lnjz-I(1),lnjtz-I(1)。

3.2 VAR模型最佳滞后阶数

滞后阶数的选择影响VAR模型的参数估计,滞后阶数选择太小会导致残差自相关,模型的参数估计不具有一致性[10]；滞后阶数选择太大，虽可减弱序列残差自相关，但会降低自由度，影响模型参数估计的有效性。因此，模型的参数估计对滞后阶数的选择有着严格的要求。

本文根据LR、FPE、AIC、SC和HQ5个指标进行选择，优先考虑AIC和SC值，由表3中的结果可知，5个指标均在滞后二阶时达到最优，因此确定最佳滞后阶数为2。

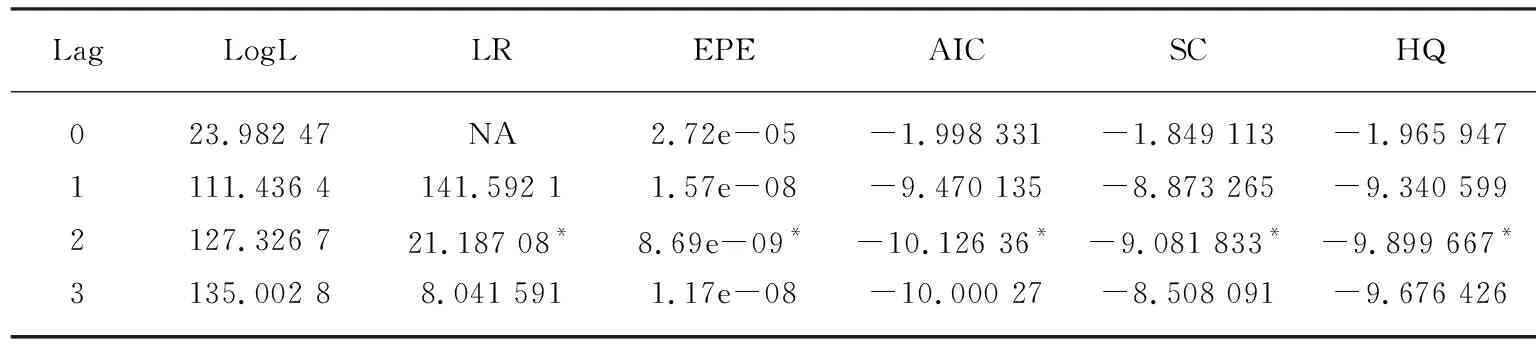
表3 最优滞后期检验结果

注：*表示超过正常值的数值

3.3 Johansen协整检验

已知建筑业投入、产出和经济增长3个变量为一阶单整，如果能证明其具有协整关系，即这3个非平稳变量的线性组合是平稳的，那么就可以确定这3个变量之间有长期稳定的均衡关系。Johansen协整检验和EG协整检验是时间序列间协整检验的主要方法。Johansen协整检验优于EG协整检验，因为Johansen协整检验不需要划分内外生变量，而基于单一方程的EG协整检验则要进行划分；Johansen协整检验可以列出变量间的所有协整方程，而EG多用于检验两个变量间的协整关系，当变量多于两个时，使用Johansen协整检验。假设协整方程有线性趋势但只有截距，滞后阶数取2，Johansen协整检验最终结果如表4所示。

表4 Johansen协整检验结果

协整检验取5%临界值为判断标准，由表4可知，迹统计量39.837 5>29.790 1，表明这3个变量间至少存在一个协整关系，13.904 8<15.494，表明至多存在一个协整关系，所以3个变量之间存在有且只有一个协整关系。同理，最大特征统计量25.937 2>21.131 6，10.704 9<14.264 6，也得出同样结果。由此可知，这3个变量间存在长期平稳的协整关系。

由协整检验还可以看出,建筑业投入、建筑业产出与经济增长之间对应的协整方程:

lnGDP=0.1025lnjtz+0.6263lnjz

由协整方程知，从长期看建筑业投入每增长1%，经济增长0.102 5%，建筑业产出每增长1%，经济增长0.626 3%。

3.4 向量误差修正模型[11]

令yt=(y1t,y2t,…,ykt)′为k维时间序列，t=1,2,…,T，yt～I(1), 即每一yit～I(1)，i=1,2,…,k，如果yt不受d维外生的时间序列xt=(x1tx2t..xdt)′限制，则有

yt=A1yt-1+A2yt-2+…+Apyt-p+ut，t=1,2,…,T

(1)

将(1)式进行协整变换得：

(2)

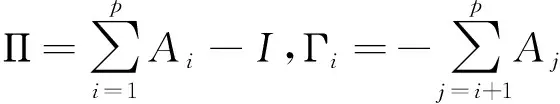
若yt存在协整关系，那么Πyt-1～I(0),此时有：

(3)

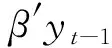
(4)

(4)式即为向量误差修正模型(VEC),其中每一方程都是一个误差修正模型(ECM)。

作为解释变量的差分项Δyt-i(i=1,2,…,p-1)的系数向量Γi(i=1,2,…,p-1)，反映的是各变量的短期波动Δyt-i对解释变量yt的短期变化Δyt的影响[8]。

由Johansen协整检验已知建筑业投入、产出和经济增长3个变量间存在长期协整关系，短期内3个变量间关系如何，还需要借助向量误差修正模型进行探究，误差修正模型的结果见表5。

表5 误差修正模型估计结果

注：ECM表示误差修正项,[]中为t值

由误差修正模型可知，误差修正项与建筑业投入、产出和经济增长这3个变量滞后项组合对经济增长有比较好的解释能力，差分后的一阶滞后效果好于二阶滞后，调整R2约为0．797；而对于lnjtz和lnjz的解释能力相对弱一些。从表5可以看出，建筑业投入和建筑业产出对GDP增长的短期弹性分别为0.180 737和0.089 187，即建筑业投入和建筑业产出每增加1%，短期可以分别拉动GDP增加约O．18%和0.09%。

3.5 基于VEC模型的Granger因果关系检验

由表6检验结果可知，国内生产总值lnGDP在10%的显著性水平下是建筑业固定资产投资lnjtz的Granger原因，但不是建筑业总产值lnjz的Granger原因；在5%的显著性水平下建筑业固定资产投资lnjtz是国内生产总值lnGDP的Granger原因，在10%的显著性水平下建筑业固定资产投资lnjtz是建筑业总产值lnjz的Granger原因；而建筑业总产值lnjz既不是国内生产总值lnGDP的Granger原因,也不是建筑业固定资产投资lnjtz的Granger原因。这说明建筑业投入与经济增长存在双向Granger因果关系，且建筑业投入是建筑业产出的单向Granger原因。

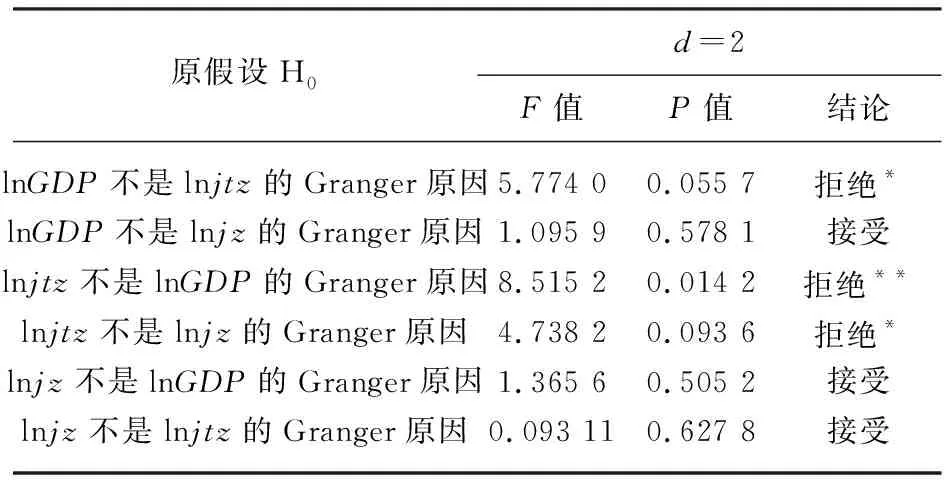
表6 Granger因果关系检验结果

注：d为滞后期，*代表10%显著性水平拒绝原假设，**代表5%显著性水平拒绝原假设。

3.6 脉冲响应函数

借助图1的脉冲响应函数对建筑业投入产出状况与经济增长间交互影响的过程进行分析。通过脉冲响应函数来分析一个标准差大小的冲击对内生变量lnGDPt、lnjtzt与lnjzt现期及未来各期的影响，并以此来考察1991—2014年间建筑业投入、产出状况与经济增长间交互影响的过程。

由图1第一行3个图可知，向量自回归模型中，给lnGDP变量当期一个标准扰动之后，通过变量之间的动态联系，对当期以后的各变量将会产生连锁变动效应，经济增长对自身的扰动脉冲响应为正，前两期有明显上升，可见短期内经济增长对其自身有很强的拉动作用，往后各期维持在0.06左右，第10期后趋于平稳。给建筑业投资一个正向冲击，经济增长第一期响应为零，之后一直处于上升趋势并到第7期达到峰值后趋于稳定。当建筑业产出受到一个正向冲击时，经济增长前4期近乎为零，第4期后有个大幅的正向反应，并在第10期达到峰值后趋于平稳。可见建筑业投入和建筑业产出均对经济增长有正向的拉动作用，短期内建筑业投入比建筑业产出的拉动效应更明显。由第二行的3个图可知，建筑业投入在经济增长受到一个正向冲击时，第1期为负，第2期上升为正并一直呈小幅上升趋势，在第9期以后趋于平稳。建筑业投入对自身的冲击前两期稳定在0.05，从第3期开始上升并于第6期到达峰值后小幅下降趋于平稳。对建筑业产出一个正向冲击后，前两期为零，可见短期内建筑业产出对建筑业投入没有影响，而从第3期开始大幅上升在第9期达到峰值并趋于平稳。由第三行的3个图可知，建筑业产出在经济增长受到一个正向冲击后，前3期大幅上升后又连续3期下降然后从第6期开始小幅上升后平稳在0.065左右。当建筑业投入受到一个正向冲击时，前两期上升，第3期下降后又大幅上升，一直到第8期到达峰值0.06后小幅下降并平稳。可见，短期内建筑业投入就对建筑业产出有拉动作用，从中长期看这种拉动作用更明显。建筑业投入对自身的冲击，前3期下降，从第3期开始呈上升趋势，并在第10期到达峰值0.07后小幅下降后趋于平稳。

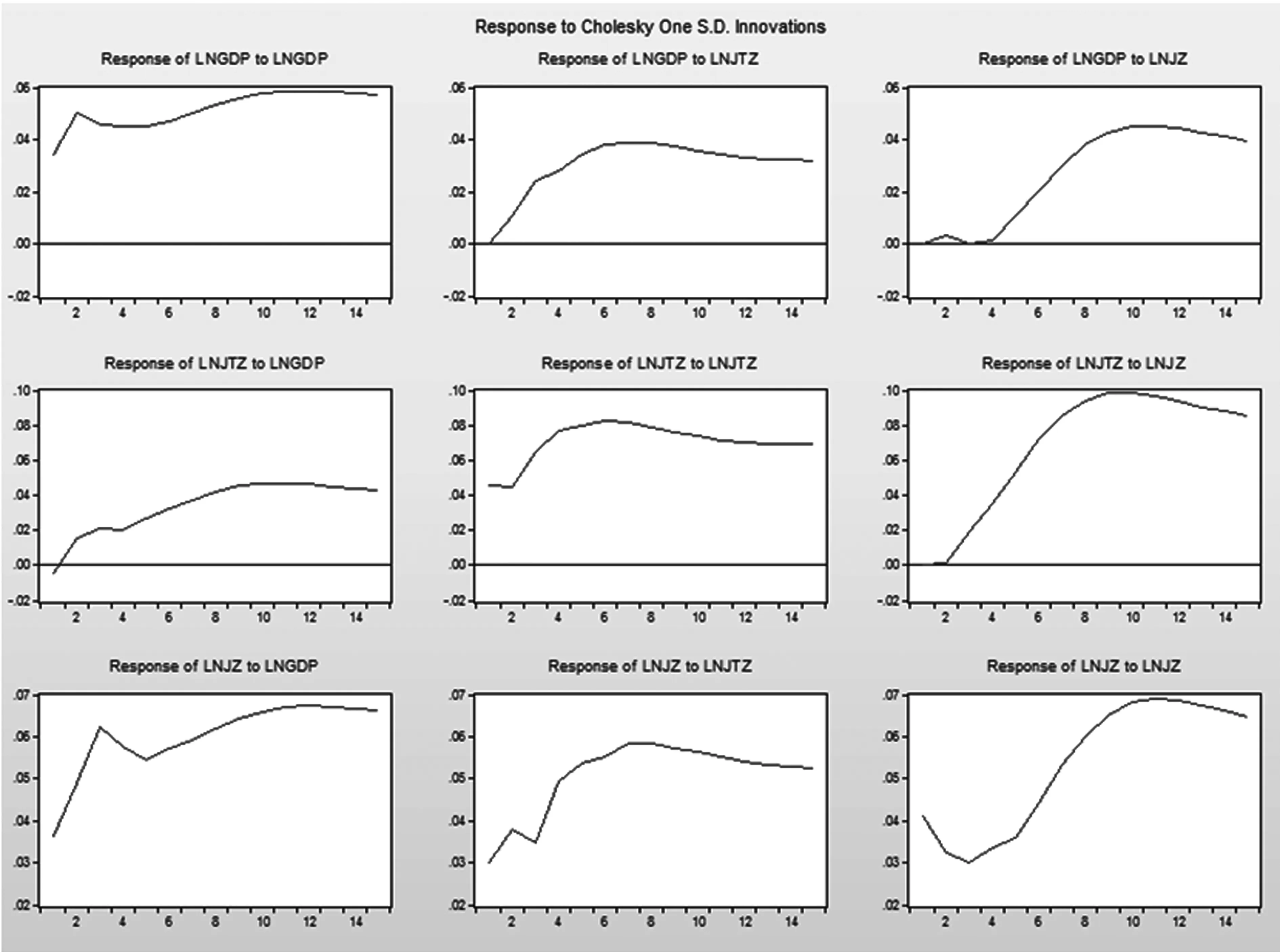
图1 建筑业投入、产出与经济增长脉冲响应函数图

3.7 方差分解

VEC模型动态特征是通过方差分解来实现的，方差分解是将模型中各个内生变量(记为m个)的变化情况按形成原因分解为与各方程互相联系的m个组成部分[5]。它实际上是一种样本外的因果检验，即当一个变量受到冲击后产生均方差，再将其分解为模型中各变量的随机冲击所做的贡献，接着得出各个变量冲击的贡献占总贡献比重，进而看出各预报误差对模型内生变量的相对重要性[6]。

运用方差分解进行建筑业投入、产出与经济增长间的相互贡献率分析(见图2)。

(1)各变量对经济增长的贡献率。由图2第1行3个图可知，国家经济增长自身方差贡献率在长期内保持在60%上下，可以看出影响国家经济增长最重要的因素是其自身，这表明国家宏观经济政策的贯彻与执行对可持续的发展有重要作用。短期内建筑业投资对经济增长影响呈上升趋势，在中长期贡献率更达到25%左右，而建筑业产出短期内对经济发展几乎没有影响，长期内有13%左右的贡献率。这说明，在重视提高建筑业投入的质量和效益的同时，也要兼顾建筑业产出的效率，加强建筑业技术创新和机械化程度，提高工程项目管理质量，才能增加经济增长速度。

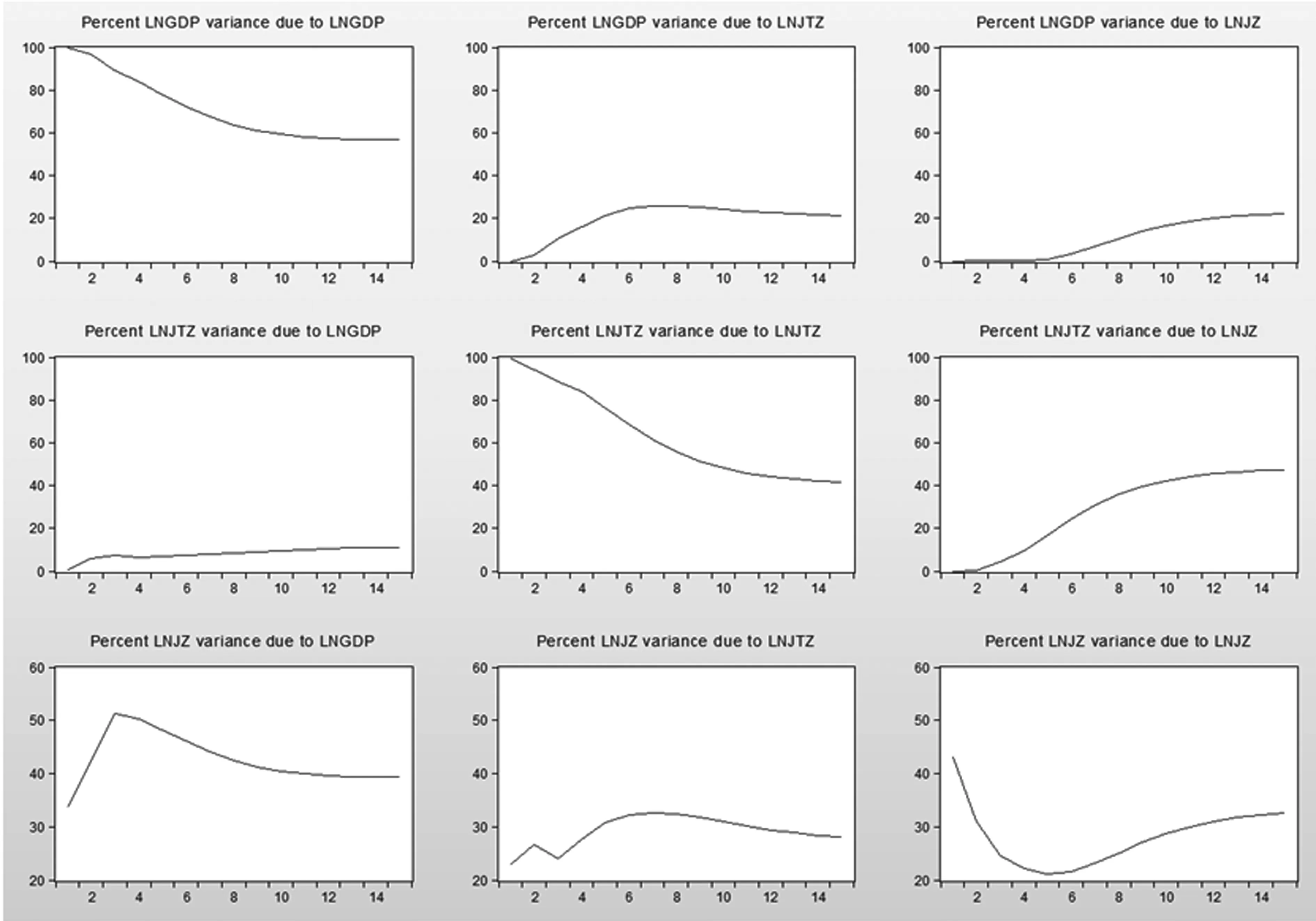
图2 模型方差分解图

(2)各变量对建筑业投入的贡献率。由图2第2行3个图可知，建筑业投入受其自身方差贡献率的影响中期内下降，长期保持在48%左右。而经济增长在短期内呈上升趋势，中期和长期内都维持在7%左右。建筑业产出对建筑业投入的贡献率中短期内呈上升趋势，长期稳定在40%左右。从长期来看建筑业投入的增长要靠自身和建筑业产出来拉动。

(3)各变量对建筑业产出的贡献率。由图2第3行3个图可知，短期看经济增长对建筑业产出的方差贡献率增长显著，最高时达到50%，中长期看呈下降趋势并最终稳定在40%左右，建筑业投入短期内呈上升趋势，中期内稳定在30%左右。而建筑业产出对其本身的贡献率短期内较高但一直处于快速下降趋势，这说明短期内建筑业产出自身方差贡献不显著，在中长期内呈上升趋势并稳定在27%左右。从长期看经济增长是建筑业产出的主要影响因素。

4 结 论

本文从建筑业投入和产出角度对其与经济增长的关系进行了实证研究，借助Eviews 8.0软件分析了1991—2014年间各变量相关时间序列，以ADF法检验各变量序列稳定性，再采用Johansen协整检验来考察变量间的长期协整关系，在此基础上构建VEC模型来检验变量间Granger因果关系和短期动态关系，在VEC模型中进行均方误差分解。得出以下结论：

(1)从长期趋势看，建筑业投入、产出和经济增长存在长期的协整关系，建筑业投入和产出对经济增长的长期弹性分别约为0.102 5%和0.626 3%，即：建筑业投入每增长1%，经济增长0.102 5%；建筑业产出每增长1%，经济增长0.626 3%，具有同向性。

(2)通过VEC模型可知，建筑业投入和建筑业总产值对GDP增长的短期弹性分别为0.180 737和0.089 187，即建筑业投资和建筑业总产值每增长1%，短期内分别拉动GDP增长约0.18%和0.09%。由此可以看出，建筑业建设周期较长，从建筑业产出角度看，短期内对经济的拉动作用没有长期内明显，而建筑业投入涉及房地产市场的开发、营销和售后服务，房地产属于第三产业，前期的项目可行性研究、房屋的预售、开发前后的融资和利益分摊等都极大地促进了资本的流动，所以短期内建筑业投入对经济增长的拉动作用比长期内更明显。

(3)Granger因果关系检验表明，建筑业投入与经济增长存在双向的Granger因果关系，并且建筑业投入是建筑业产出的单向Granger原因。这说明，建筑业投入能有效促进国家经济增加，同时经济增长对建筑业投入具有反向拉动作用。经济增长促进了收入的增加，进而也直接增加了建筑业投入，使建筑业得以发展。同时，建筑业投入的增长也促进了建筑业产出的增长，因为随着投入的增加，更多的生产要素参与到建筑业的生产中，建筑业规模效应日益体现。但鉴于我国建筑业整体的高投入、高消耗和低效益的发展现状，建筑业产出构不成建筑业投入的Granger原因。

(4)利用方差分解图从方差贡献率的角度可以看出，建筑业投入对经济增长的贡献率要远大于经济增长对建筑业投入的贡献率，而建筑业产出对经济增长的贡献率却要远小于经济增长对建筑业产出的贡献率。总体来看，经济增长和建筑业投入自身方差贡献占主导，而建筑业产出的方差贡献率的主要变量是经济发展。