解析几何问题的创新解法从哪里来
王成杰 刘新春
(1.江苏省扬中高级中学 212200;2.扬中市教师发展中心 212200)
我们常常惊叹于各种数学杂志资料上介绍的数学问题的精妙解法,我们也偶尔对自己灵光闪现发现的优美解法洋洋得意,我们更为教学中学生创造的层出不穷的奇妙解法所吸引,感叹数学解题方法真是没有最好只有更好.冷静下来,我们不禁要问:创新解法你从哪里来?构建充满联系的知识结构,探究问题背后的本质规律,掌握解决问题的基本策略,反思解题方法的缺陷不足,坚持策略方法的不断改进,捕捉奇思妙想的灵感闪现,创新解法往往会不期而遇.以下以解析几何问题的求解为例,探究如何发现创新解法.
1 显现隐含条件
在许多解题实践中,我们常常被多种题设条件的表面含义所遮蔽,而发现不了这些条件背后的隐含条件,更发现不了隐含条件背后的最核心的原理,只能就事论事.“直译”条件造成解法繁琐,运算复杂.甚至无法求解.破译隐含条件,打通条件与结论的最简通道,则优美解法就会水到渠成.
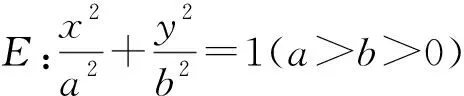
(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
分析本题主要考察直线方程,直线与直线的位置关系,椭圆方程,椭圆的几何性质等基础知识,考察分析问题、解决问题能力和运算求解能力.常规解法如下:
解析1(1)设椭圆的半焦距为c,
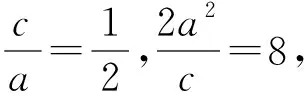
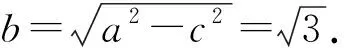
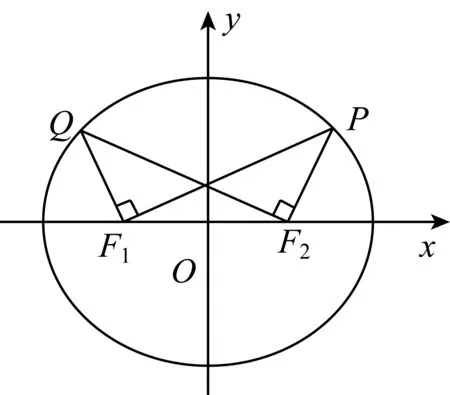
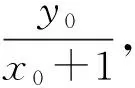
①
直线l2的方程:
②
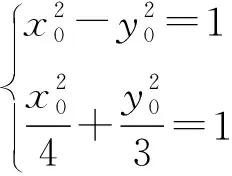
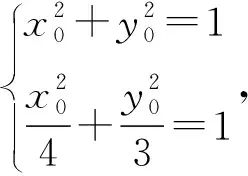
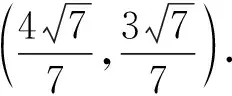
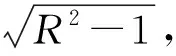

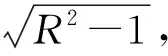
从这一分析过程可知,本题中发现优美解法的关键隐含条件就是P,Q是经过椭圆焦点的圆与椭圆的交点,且是圆M的直径端点,发现了这一隐含条件,简捷解法跃然纸上.
2 优化图形结构
解析几何的源泉是几何,图形是直观表现形式,是问题的起点和归宿,而代数方法仅仅是工具,看穿图形的整体结构和本质特征就能大道至简,“一招封喉”,化繁为简,发现隐含图形之中的简单方法.
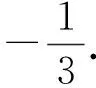
(1)求动点P的轨迹方程;
(2)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
分析(1)动点P的轨迹方程易得x2+3y2=4,(x≠±1),解题过程略.
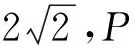
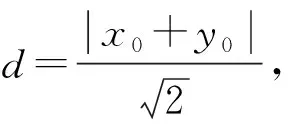
=x0+y0,
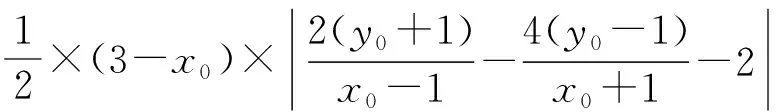
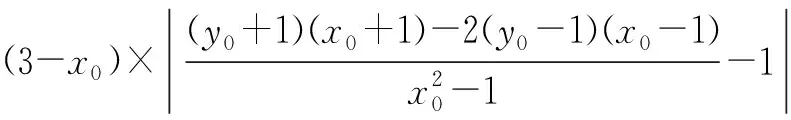
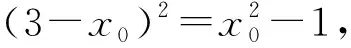
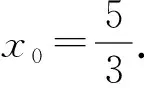
以上解法着眼于从两个三角形的边与高的数量关系出发,表示两个三角形的面积.如若抓住两个三角形的一对对顶角,则可另辟蹊径表示三角形面积,获得解法2.
解法2由S△ABP=S△PMN,可得S△APB=
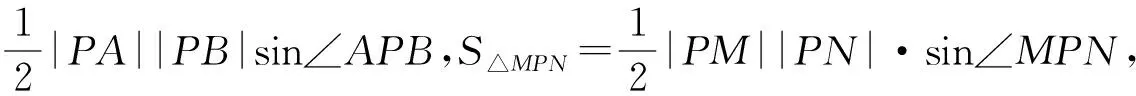
(xP-xA)(xP-xB)=(xN-xP)(xM-xP),
即(xP+1)(xP-1)=(3-xP)(3-xP),
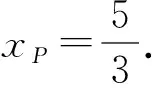
上述两种解法瞄准了几何图形的局部和细节(边或角)获得解法.如能跳出细节,着眼于从几何图形的整体结构出发,通过等积变换,发现几何图形更进一步的几何特征——点P是△ADN的重心,由于点A,D,N的横坐标已知,因而能便捷地求出P点的坐标.
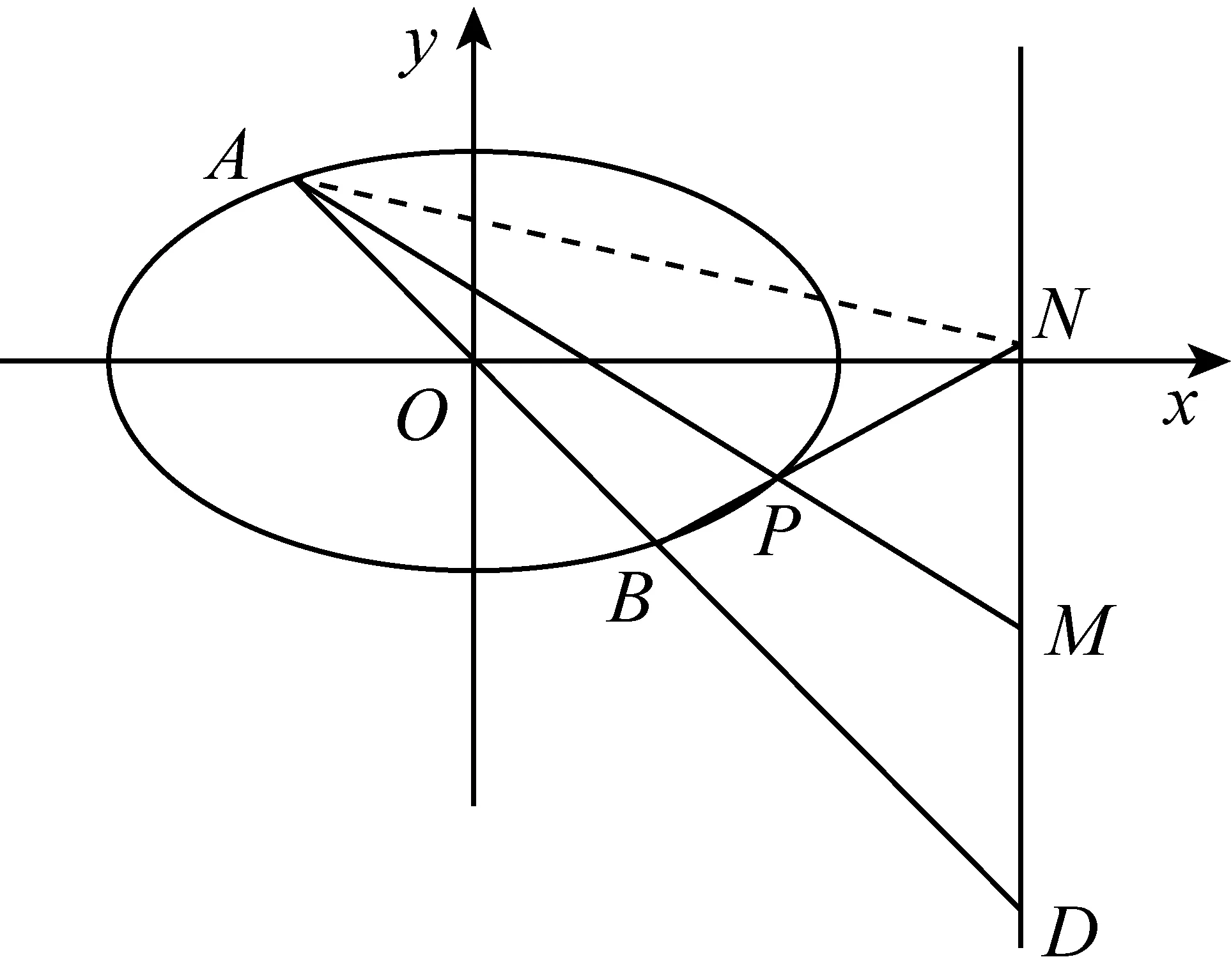
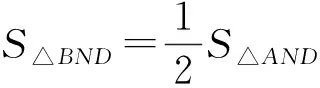
在上述解法3中,我们从图形的整体结构出发,在△ADN中,从△PAB与△PMN的面积相等、B为AD中点、M为ND中点,结合分析得到P是△ADN的重心,获得运算量很小的解题方法.
3 妙用曲线性质
解析几何的两大任务就是建立曲线的方程和运用曲线方程研究曲线性质. 如若借助已经获得的曲线性质探究解题思路,则往往会发现意料之外的惊喜.

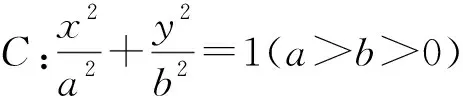
(1)求椭圆C的标准方程;
(2)设直线PA的斜率为k1,直线MA的斜率为k2,求k1·k2的取值范围.
分析破解本题的关键是表示出两直线PA,MA斜率的乘积k1·k2,首先确定选哪个参数作为变量,一般可选择点的坐标作为参数,或者斜率作为参数,以下方法一就是以点P的坐标作为变量,从而分别得出直线PA,MA的斜率,进而表示出k1·k2.
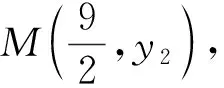
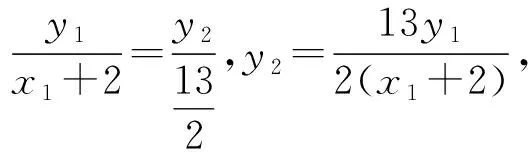
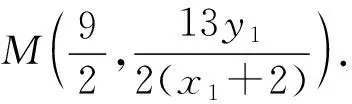
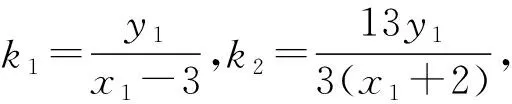
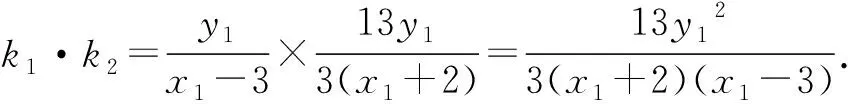
因为点P在椭圆C上,
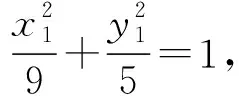
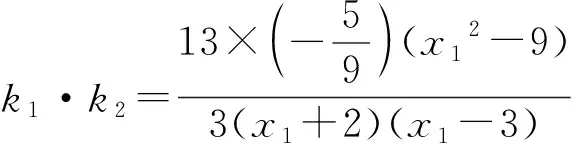
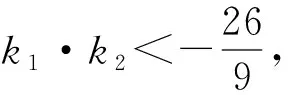
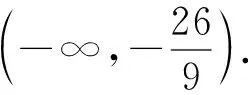
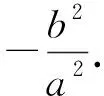
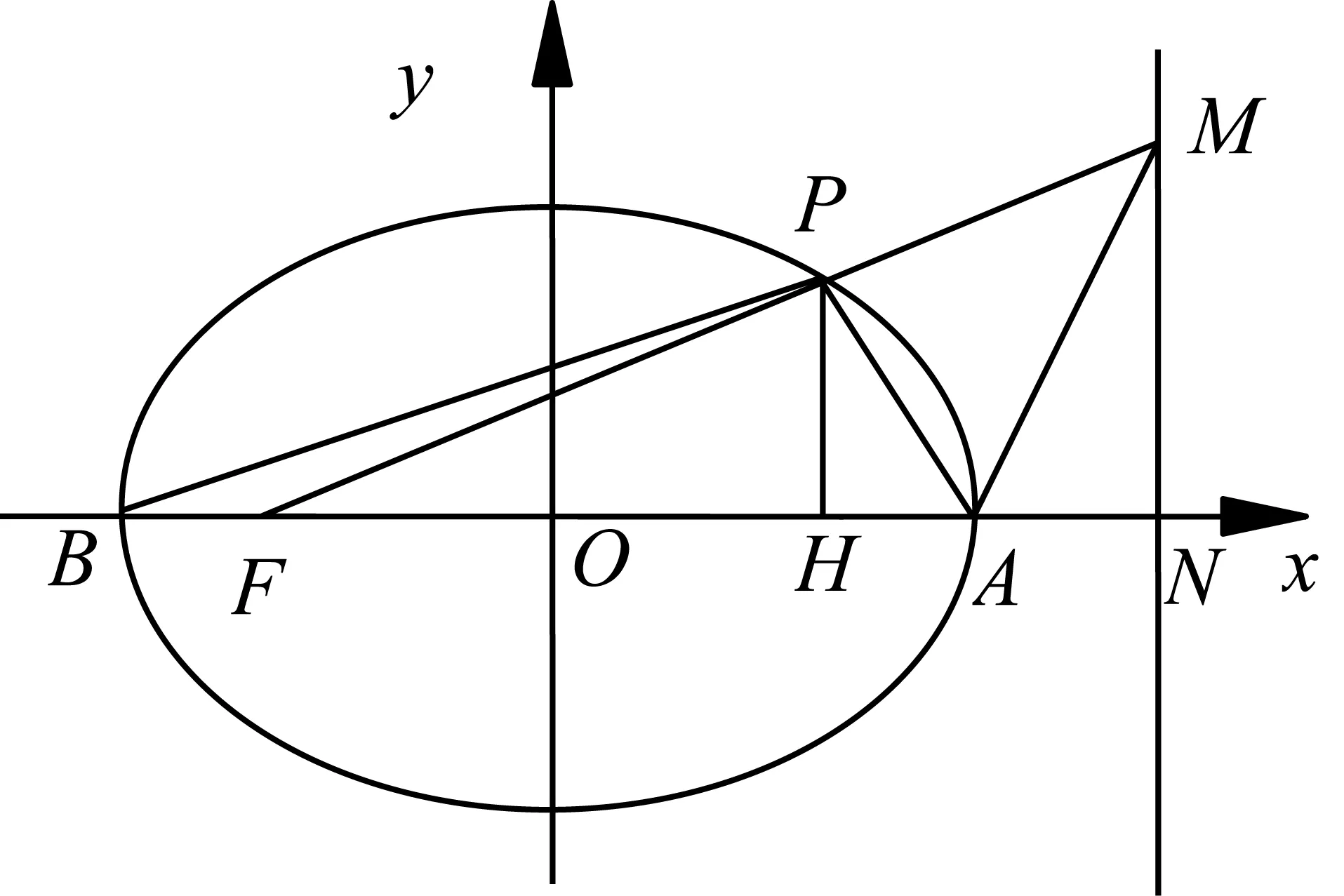
解法2记椭圆的左顶点为B,过点P作x轴的垂线,垂足为H,连接PB,PH.设P点的横坐标为x0,则-2 将①,②,③的左右两边分别相乘即得 比较上述两种解法可知,正确运用椭圆的性质,既能迅速发现解题思路,又能简化解题步骤,减少运算量. 在同一个问题中往往会出现多个条件,而同一个条件又可以有多种表征方式,用不同的表征方式表达条件往往影响解题思路的发现,决定解题方法的优劣,一个条件的不同表征方式与其它条件连结时,连结方式往往不同,难易繁简差异也很大,如果一个问题中的各个条件能用恰当的表征方式优化组合,就能获得更佳解法. (1)求椭圆C的方程; 对比两式相差2x1y2x2y1,故将前式变形为 (x1x2+2y1y2)2+2(x1y2-x2y1)2=4,把三角形的面值代入即有x1x2+2y1y2=±1, 整理得t2(x1x2+2y1y2)=4-2t2,意外的惊喜出现了. 因为A,B点在椭圆上, 两式相乘得 配方变形得 (x1x2+2y1y2)2+2(x1y2-x2y1)2=4, x1x2+2y1y2=±1, 又因为点E是A,B的中点, 由x1x2+2y1y2=-1,得t2=4,t=2, (1)求椭圆C的标准方程; (2)如图,过点C(0,1)且斜率大于1的直线l与椭圆交于M,N两点,记直线AM的斜率为k1,直线BN的斜率为k2,若k1=2k2,求直线l斜率的值. 分析第(1)问略,对于第(2)小问,一种基本思路是:先设出直线AM的方程,与椭圆方程联立,由于两交点中点A已知,根据韦达定理得出点M的坐标,同理得出点N的坐标,由于直线MN经过定点C(0,1),由三点共线可求出k1,k2之间的一个等量关系式,再与条件k1=2k2联立方程组,可解出k1(或k2)的值,从而求出直线MN的斜率. 消去y可得: 点评这一思路的获得很自然,但其过程运算量非常大,容易出错.能否不求M,N点的坐标,减少一些复杂的运算?由于直线AM和BN与椭圆的交点也是直线MN和x轴与椭圆的交点,因此可以直接由直线AM和BN的方程与椭圆方程联立得到直线MN的方程,从而减少运算量. 解法2由题意得:AM直线方程为y=k1(x+2),即k1(x+2)-y=0①, BN直线方程为y=k2(x-2), 即k2(x-2)-y=0②. 将①与②左右两边分别相乘有k1k2(x2-4)-y[(k1+k2)x+2(k1-k2)]+y2=0③, 由于直线MN经过定点C(0,1), 1.从以上几例可以发现,如果我们对数学问题的条件进行横向、纵向、递进式、螺旋式、多角度的转化,就像剥竹笋一样,层层剥去外壳,就会越来越接近问题的内核——本质规律和最简单明了的结论,从而快速发现简捷的方法. 2.图形直观是发现优美解法的又一法宝,因为图形具有整体性、对称性、简约性和美感等特点,能够快速激活人的直觉思维、简缩思维、形象思维和联想思维,从整体上迅速连接题目中的各个条件并加以优化,更容易选择优化的解题思路,甚至获得创新解法. 3.“扬长补短,消灭短腿”.在教学实践中发现成绩差的学生经常也会提出创新的解法,分析原因是因为这些学生往往在某一方面的知识方法思维比其他学生强,当题目的条件结论与他们的强项结合时就容易产生优美的解法.因此在实际教学中,我们既要不断地对学生进行“补短”教育,更要进行“扬长”教育,只有扬长才能激活创造潜能.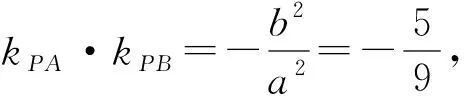

4 多元表征条件
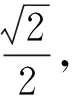
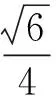
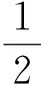
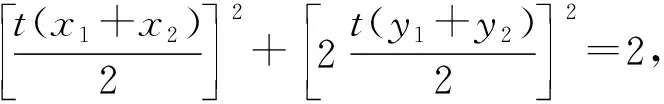
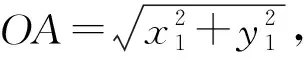
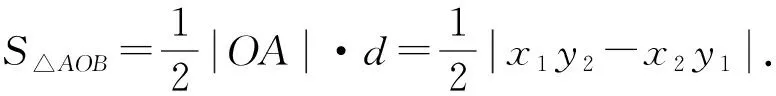
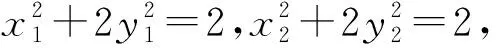
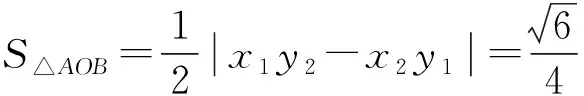
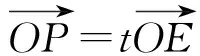
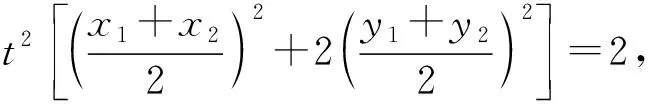
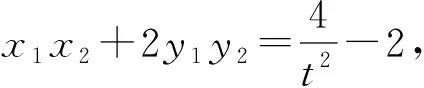
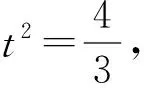
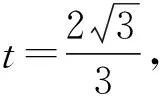

5 妙用逆向代换
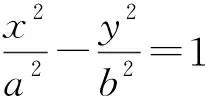
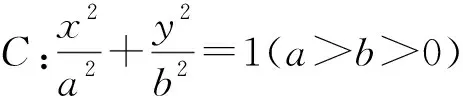

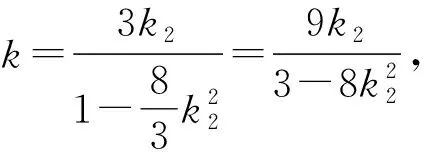
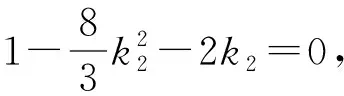

几点启示

