解题反思：实现学生自我提升的有效路径

蒋 凯

(苏州胥江实验中学 215004)

我们知道，问题是数学的心脏．如何切实提升学生解决问题的能力，从而让学生轻负高效地进行数学学习，则需要培养学生养成良好的解题反思习惯．但是在解题之后具体反思什么，如何进行反思，教师往往缺乏系统的思考，学生往往只是停留在低层次的错题整理上．笔者认为，在指导学生解题反思之时，教师有必要从以下几个角度引导学生学会反思，进而促成学生自我提升与发展，帮助学生找到实现自我提升的有效路径.

1 反思解题所用的基础知识、数学思想方法

在问题讲解过程中，引导学生围绕基础知识进行回顾总结，可以使学生对知识理解更加深刻．而对初中学生进行必要的数学思想方法的渗透，可以在解题实践中切实引导学生体验思想方法对解题的指导作用.

例1二次函数y=ax2+bx+c(a≠0)的图像如图1所示，请根据图像解答下列问题：

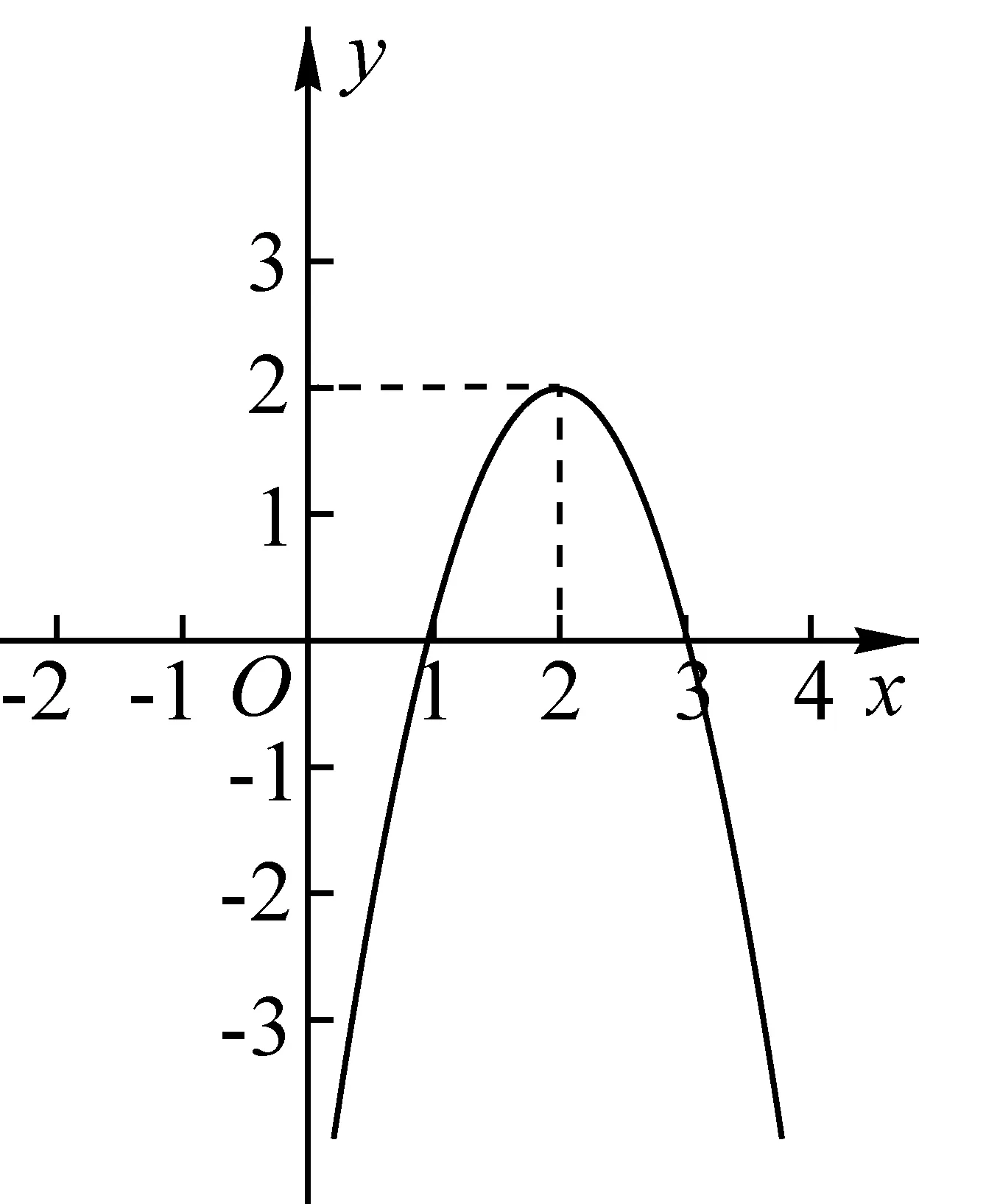
图1

(1)写出方程ax2+bx+c=0的两个根.

(2)写出不等式ax2+bx+c>0的解集.

(3)若方程ax2+bx+c=k有两个不相等的实数根，求k的取值范围.

反思求方程ax2+bx+c=0(a≠0)的两根，即为求二次函数y=ax2+bx+c的图像与x轴的交点的横坐标；求不等式ax2+bx+c>0(a≠0)的解集，即为求二次函数y=ax2+bx+c的图像在x轴上方时自变量x的取值范围；研究方程ax2+bx+c=k(a≠0)的根的情况，则等价于研究过点(0，k)且平行于x轴的直线y=k与二次函数y=ax2+bx+c的图像的公共点情况．诸如此类的反思与总结，无论是对问题解决的策略概括与提升，还是对学生数学思想方法(数形结合)渗透意识的形成，都将大有裨益．

2 反思解题所用的基本技能、特殊解题技巧

在教学实践中，我们经常发现，不少学生对问题的分析很到位，解题思路和方法也正确，但由于技能相对薄弱，或者缺少必要的解题技巧，最终导致解题失败．由此可见，反思解题过程中所用的技能、技巧也很有必要.

例2(苏州中考题) 设抛物线y=ax2+bx-2与x轴交于两个不同的点A(一1，0)、B(m，0)，与y轴交于点C，且∠ACB=90°.

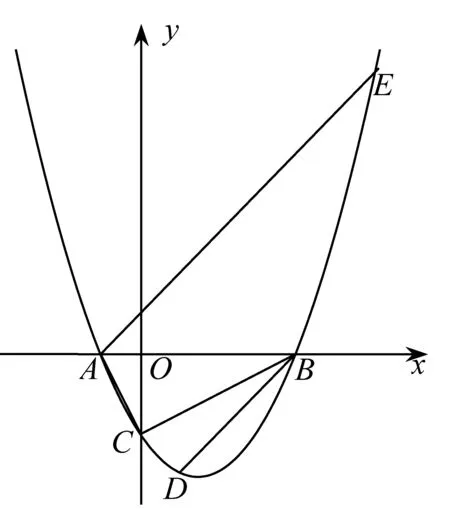
图2

(1)求m的值和抛物线的解析式；

(2)已知点D(1，n)在抛物线上，过点A的直线y=x+1交抛物线于另一点E．若点P在x轴上，以点P、B、D为顶点的三角形与△AEB相似，求点P的坐标.

(3)在(2)的条件下，△BDP的外接圆半径等于______.

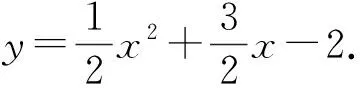
由“y=ax2+bx-2”得到C(0，-2)，这样的技能应成为一种自动化反应；由“∠ACB=90°、OC⊥AB”想到△ABC、△COB、△ACO这三个三角形两两相似，这样的想法应成为一种思维习惯；由“△ABC为直角三角形”想到分类讨论(尽管符合题意的只有一种情形)，应该成为学生的一种基本素养．当技能成为自动化反应，一定条件的组合能够唤醒学生的知识储藏，一定的条件特征能够得到一定的思维呼应，那么基本技能也就固化成内在的数学品质，特殊的解题技巧也就应时而生了．

3 反思解题经历的探究过程，从感性解题思维进入理性阶段

先秦寓言《列子·汤问》告诉我们：学习，不仅要知其然，而且还要知其所以然．因此，我们要善于观察和认知事物，并掌握其规律，从而知道事物是怎么样的，为什么是这个样子的．也就是说，看待事物更要看到本质．在解题教学中，我们要引导学生反思“为什么要这么想”即“从题目中的何种信息引导我们这么想”，从而使学生对一道难题的感性认识上升到解题策略提升的理性思维阶段.

例3有一个二次函数的图像，三位学生分别说出了它的一些特点：

甲：对称轴是直线x=4；

乙：与x轴两个交点的横坐标都是整数；

丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3.

请你写出满足上述全部特点的一个二次函数解析式：________.

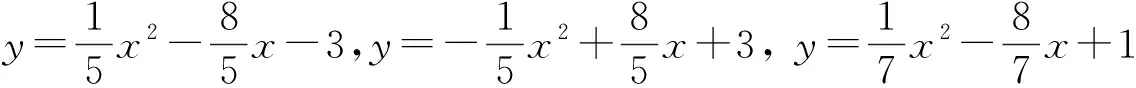
4 反思解题过程中的易错点，在突破思维定势中对审题重要性的认识

在解题过程中，不少学生由于对基础知识理解不够深刻，或者审题不够仔细，从而造成解题错误．因此反思解题过程中的易错点，突破固有的思维定势，其实也是给自己提供一个对基础知识重新理解的机会.

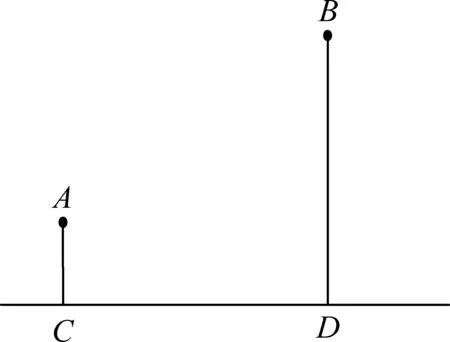
图3

例4如图3，A、B两个村子在河边CD的同侧，A、B两村到河边的距离分别是AC=1千米，BD=3千米，且CD=3千米．现要在河边CD建一水厂向A、B两村供应自来水，已知铺设水管的工程费用为每千米2万元．请你在CD上选择水厂位置，使铺设水管的费用最省，并求出铺设水管的总费用.

错解如图4，作点A关于CD的对称点F，连接FB交CD于点E．则E点处即为所建水厂位置．过点F作FG⊥BD交BD的延长线于点G，易解得：FG=3千米，BG=4千米，在Rt△BFG中，求得FB=5 千米．故所铺设水管的总费用至少为2×5=10 万元.

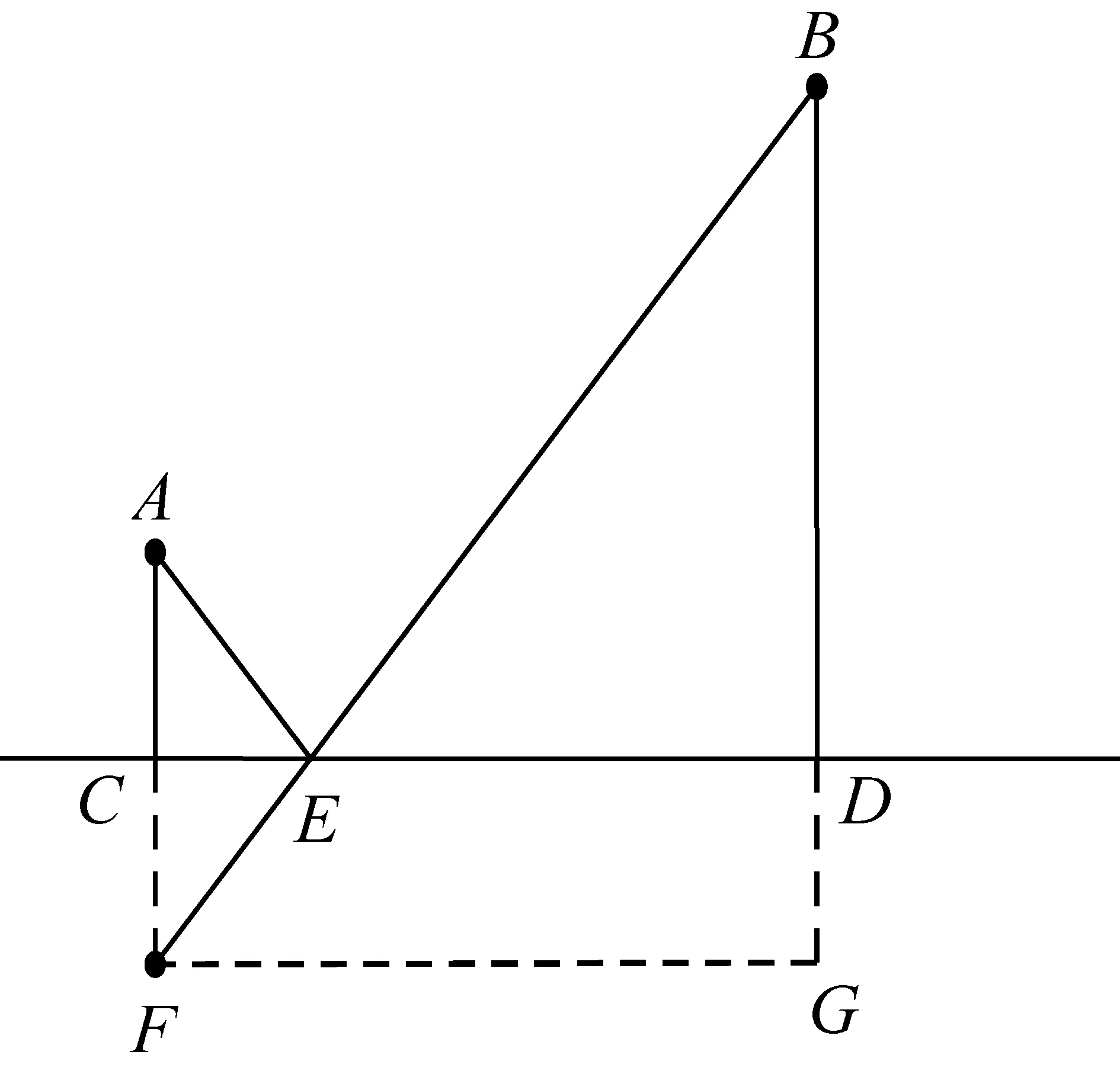
图4

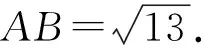
元．该方案显然比如图4所示的方案来得更为合理．从本例中可以看出，由于“思维定势”而造成的盲目“生搬硬套”，往往就是学生解题的易错点所在．从某种意义上讲，本题对促进教师自我反省以改进教学方法也是一个很好的案例．

图5

结语数学教学离不开解题，解题反思能够更好地加深学生对问题的理解，提升对所学知识的综合运用能力．当然，除了上述的几个反思角度之外，我们还可引导学生去反思某类问题的解题一般规律、问题的拓展延伸方向等等．因此，在每一次解题教学之后，教师若能恰当地引导学生对相关问题进行反思，久而久之，将会促成学生的反思意识从被动到主动，带来的是学生的解题思维从感性到理性，从模仿到自立与创新，学生的解题能力必将得到提高，从而实现陶行知先生所倡导的“处处是创造之地，天天是创造之时，人人是创造之人”之境界．