基于参数空间的伪攻角姿态驾驶仪设计*
王帅为,马清华,郑建强,杨姝君,程鹏飞,梁益铭
(西安现代控制技术研究所,西安 710065)
0 引言
从控制的角度来看,导弹制导控制系统主要包含两个大回路,即制导回路和控制回路。制导回路的任务是如何由弹目信息生成拦截目标的策略,而控制回路则是如何操纵执行机构精确,鲁棒的实现这种策略,因此内回路又称自动驾驶仪[1]。
自动驾驶仪一般分为过载自动驾驶仪和姿态驾驶仪。弹体追踪法作为一种经典的导引方法,实现简单,只需在飞行过程中使弹轴对准目标即可。但在弹道末端法向过载过大,会造成大的脱靶量,因此追踪法一般应用在交接班之前。由于其直接给出的是俯仰角指令,故与其相匹配的驾驶仪为姿态驾驶仪。
1 弹体线性模型
由系数冻结法得到弹体的线性模型如下[2]:
(1)
得到系统的传递函数:
(2)
式中:km为弹体开环增益;ξm为弹体开环阻尼;t1为攻角滞后时间常数;tm为弹体开环时间常数。flag为标志位,弹体静稳定时,标志位取1,静不稳时,标志位取-1,静中立时,标志位取0。
2 典型姿态自动驾驶仪
典型姿态自动驾驶仪如图1所示。
由图1可知,姿态驾驶仪一般由阻尼反馈和姿态角主反馈组成。驾驶仪的输入信号为俯仰角信号,由文献[3-4]可知,驾驶仪的闭环极点为一组大的共轭复根和一个小的实极点,且高频根的时间常数大于弹体的开环时间常数tm,低频根的时间常数小于弹体的开环慢时间常数t1。故该慢根成为闭环系统的主导极点,将会对制导大回路产生很大的影响。
当弹体静不稳时,为了保证内回路的稳定性,需要大的阻尼反馈,但阻尼反馈过大会带来一系列不利的影响[5-7]。
2.1 截止频率的限制
由于舵机处开环截止频率wc≫1/tm,故:
(3)
截止频率受到舵资源等硬件条件的限制,不可能过大,故kw也不可能过大。
2.2 传感器噪声的影响
角速率信号一般由速率陀螺测量得到,测量信号里包含了测量噪声和弹性振动的分量,如果反馈增益过大,噪声信号和弹性分量也会增大,将会对弹体产生不利的影响。
2.3 角速率响应的影响
角速率回路的闭环传递函数为:
(4)
其姿态角速率稳态值为:

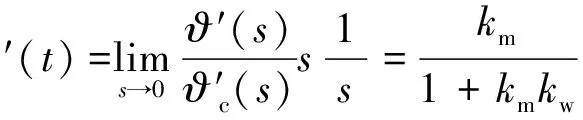
(5)
3 伪攻角自动驾驶仪
将弹体模型写成包含姿态角的增广形式:
(6)
则根据状态反馈理论,指令可写成:
δz=-kwϑ′-kαα-kp(ϑc-ϑ)
(7)
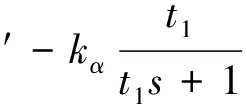
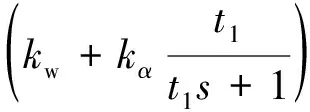
(8)
系统的框图如图2所示。
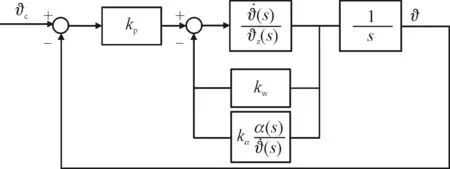
图2 伪攻角姿态驾驶仪
将式(8)代入式(1)可知:
ϑ″=a22ϑ′+a24α+a25(-kwϑ′-kαα-
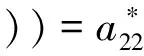
(9)
式中:
(10)
3.1 kw的影响

3.2 kα的影响
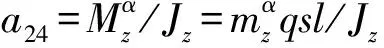
采用伪攻角方案时,姿态角速率反馈信号为:
(11)
将角速率信号先滤波,可以减小测量噪声和弹性分量的影响。
3.3 kp的影响
导弹的阻尼回路和增稳回路将弹体改善为性能良好的新弹体,外回路通过俯仰角主反馈,采用比例控制,使弹体快速,稳定的跟踪指令。为了抑制干扰,消除稳态误差,也可将比例控制改为比例积分控制。
4 参数空间设计法
考虑某单输入单输出系统:
X′=A(θ)X+B(θ)U
(12)
式中:θ为不确定对象的参数向量。则状态对输入的传递函数矩阵为:
(13)
引入状态反馈:U=-kX-uc。
则闭环系统对参考输入的传递函数矩阵为:
(14)
故单输入单输出系统的闭环方程为:
dc(s)=d(s)+kg(s)
(15)
极点配置一般是给定一组期望的闭环极点s1,s2,…,sn来计算控制增益。要求设计者准确的给出一组合适的极点并不容易,但通常对极点应该位于哪个区域比较清楚。与极点配置相比,区域极点配置有更大的自由度。
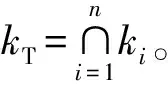
对于k的选择,可从以下几点考虑[8-9]:
1)为了减小控制量|U|,应选‖k‖较小。
2)考虑到实现时的不确定性,应选k在kT的中心。
3)对传感器失效故障具有鲁棒性。
4)增益下降所需要的裕度。
5 舵机处开环幅频特性
导弹线性模型的传递函数为:
(16)
给定三阶系统的期望闭环极点:
(17)
则由对应系数相等可得:
(18)
由式(18)可以得到控制参数的解析解,但上述结果是在忽略舵机、角速率陀螺等硬件的动态特性下得到的理论值。在低频区,其造成的相位滞后可忽略,而在高频区,根据文献[9]的思想,可以用一个等效舵机来代替弹上的硬件高频项,其影响不能忽略,因此必须保证舵机处有足够的相角裕度。
舵机处开环传递函数为:
H·G=ϑ′(kw+kαt1/(t1s+1)+kp/s)=
(19)
由于舵机处开环截止频率为wc≫1/tm,故:
(20)
代入式(18)得到:
wc+2ξm/tm=a+2ξwn
(21)
又ξm/tm≈0,故:
wc≈a+2ξwn
(22)
由于弹体阻尼非常小,忽略与ξmtm有关项,故:
(23)
定义k=a/wn,故wc=a+2ξwn=(k+2ξ)wn代入式(23),得到:
(24)
由于极点配置一般将阻尼比配置在0.5~1之间,则得到相位裕度与k的关系如图3所示。

图3 舵机处开环相位裕度
由图3可知,当阻尼比较小时,相位裕度随k的增大而增大,当阻尼比大于0.7时,裕度随k先减小后增大;对于任意的k>0,只要阻尼比大于0.5,均可保证舵机处裕度大于45°;且当k足够大时,系统的相位裕度收敛到85°左右。
考虑到闭环参考输入到舵机的传递函数为:
(25)
舵偏角的增益:
(26)
由上式可知,实极点也不宜选的过大,否则舵偏角增益kp会过大,很容易造成舵机满偏。
6 极点的选择准则
1)为了抵消分子零点的影响,将分母实根配置在分子零点附近,使其成为偶极子。取:
a∈(0.9/t1,1.1/t1)
(27)
2)最小阻尼ξmin可由规定的最大超调量来确定,近似的有:

(28)
3)为了使响应足够快,取最大阻尼ξmax≤1。
而角频率的选择很难直接提出合理的约束条件。相比之下,对舵机处的截止频率提要求更具有实际的工程意义。考虑到式(23),可直接对截止频率提要求。
4)最小截止频率wcmin:wc决定了系统的响应速度,一般选取wc至少为弹体自振频率的2~3倍。
5)最大截止频率wcmax:为了减小舵机等硬件在舵机处的相位滞后,一般选取wcmax为舵机频率的1/5~1/3。
7 姿态控制系统数字仿真
将式(24)代入式(19),得到:
(29)
把系统参数不确定性作为特征参数,在特征点处,控制系统可以看作是一多模系统。对伪攻角自动驾驶仪采用参数空间方法。舵机的带宽一般能达到150~220 rad/s。选取wc∈(15 rad/s,30 rad/s),ξ∈(0.5,1),a∈(0.9/t1,1.1/t1)。选取静不稳特征点如表1所示,并进行极限拉偏,拉偏条件为±20%,参数如表1所示。

表1 静不稳动力系数
将wc、ξ、a离散化,代入式(29),即可求出对应的参数。根据前面提到的参数选取准则,鲁棒的参数值应该选在公共区域的中心。为了便于观察,将三维区域向三个坐标平面投影,结果如图4~图5所示。
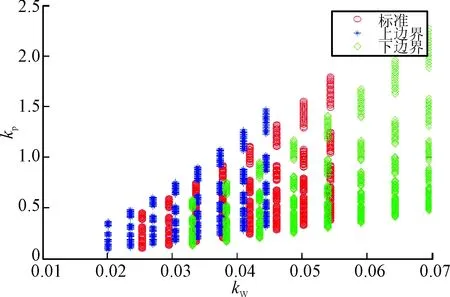
图4 静不稳特征点参数空间kw和kp设计结果
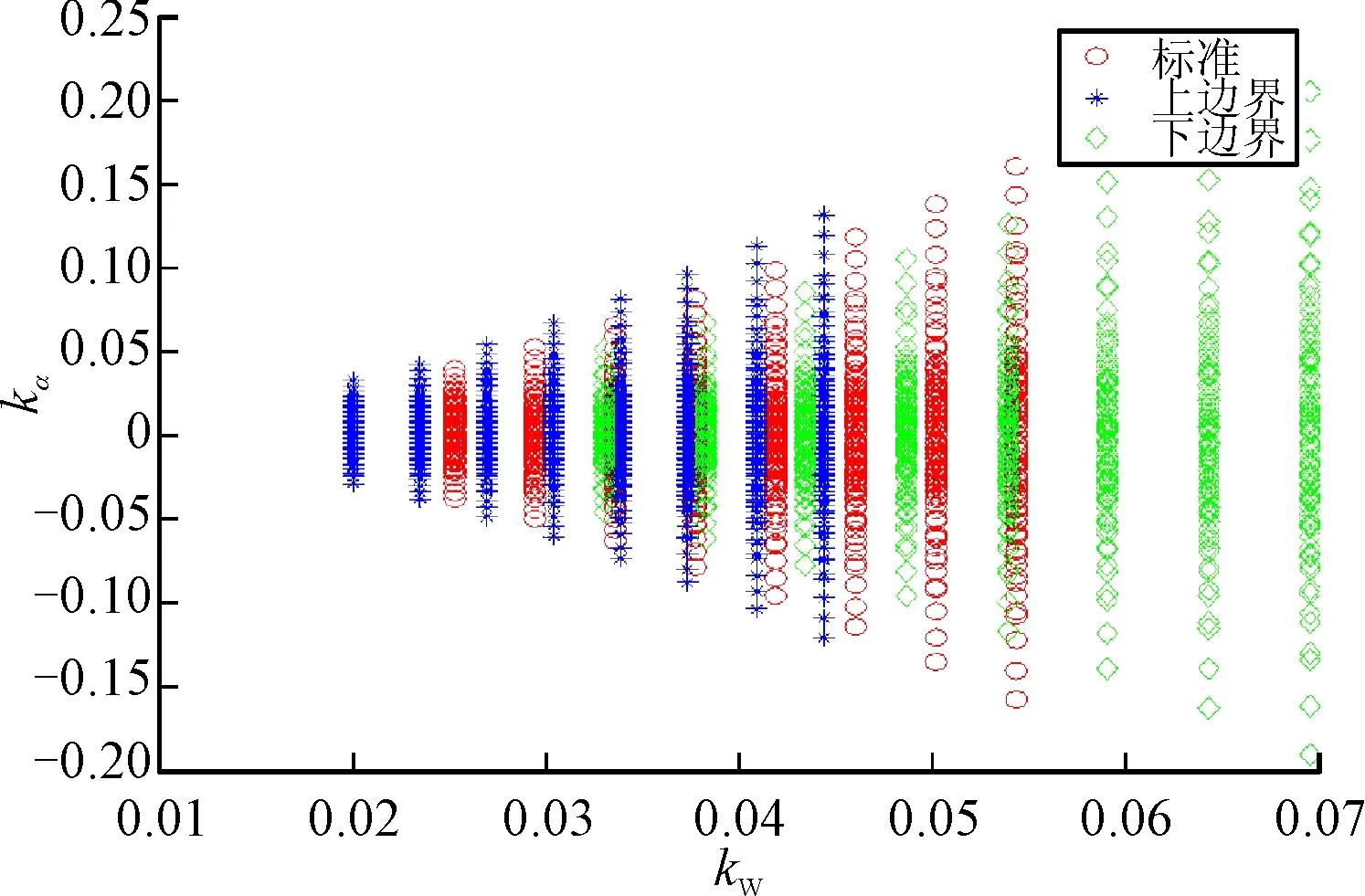
图5 静不稳特征点参数空间kw和kα设计结果
可取:kw=0.032,kα=0.079,kp=0.4。由于上述参数是在忽略舵机模型条件下求得的理想值,参数是否可行需加入舵机进行验证。考虑加入舵机环节:
(30)
式中:舵机的wn取25 Hz;τ取10 ms;ξ取0.707。阶跃响应如图6所示。
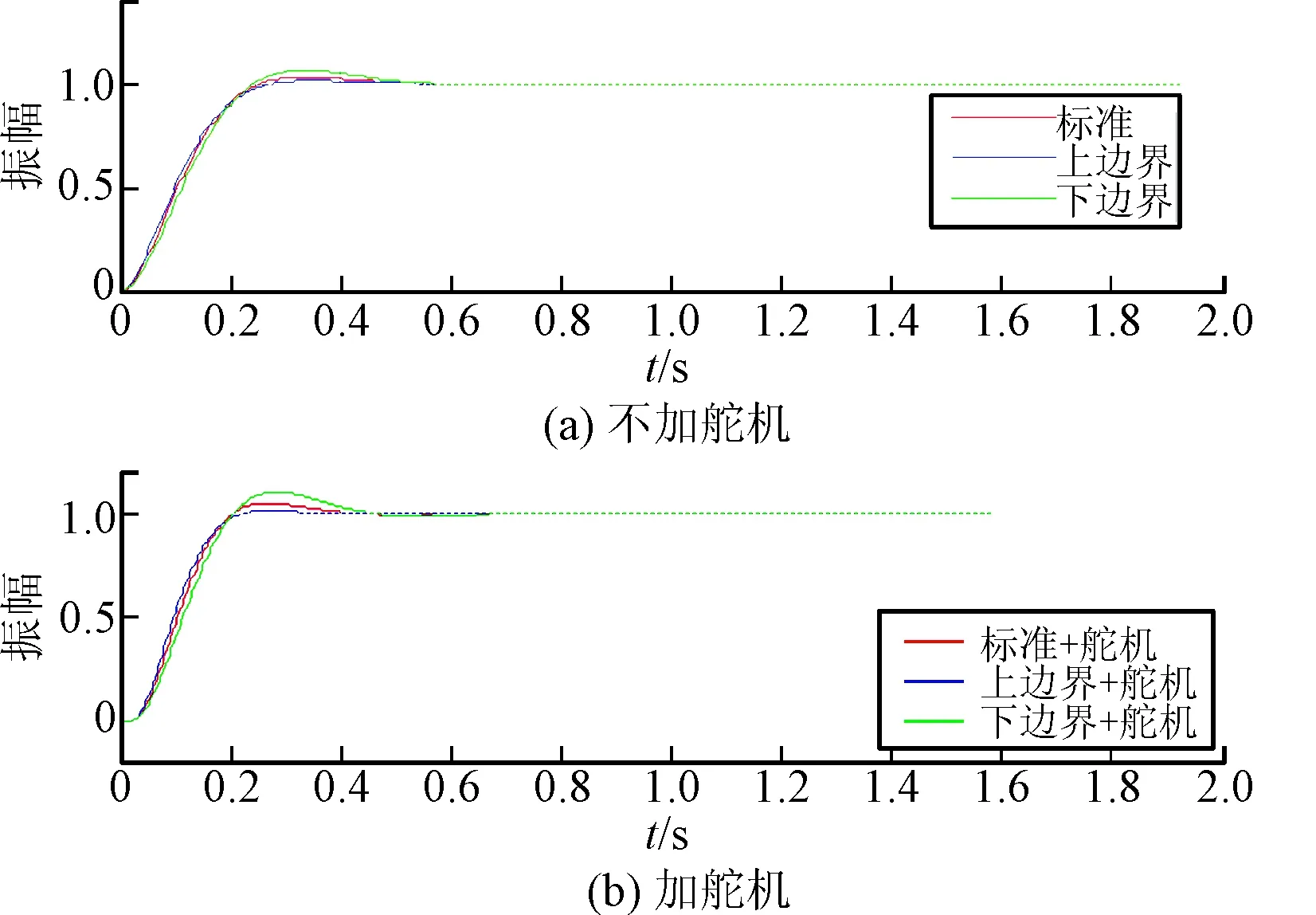
图6 静不稳定特征点加舵机与不加舵机阶跃响应
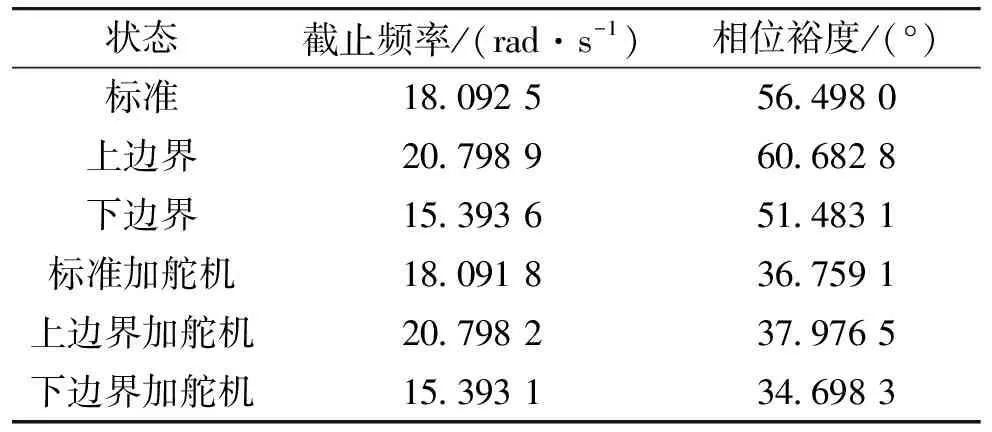
状态截止频率/(rad·s-1)相位裕度/(°)标准18.092 556.498 0上边界20.798 960.682 8下边界15.393 651.483 1标准加舵机18.091 836.759 1上边界加舵机20.798 237.976 5下边界加舵机15.393 134.698 3
由图6和表2可知,采用参数空间法设计的伪攻角姿态驾驶仪可以稳定静不稳弹体,加入舵机后仍可保证系统有足够的相位裕度,且在参数拉偏的情况下具有很好的鲁棒性。
8 结论
文中针对静不稳定导弹的姿态控制问题,采用参数空间法对伪攻角姿态驾驶仪进行了设计,得到以下几点结论:
1)通过合理的选择伪攻角驾驶仪参数,可以增大等效弹体的阻尼,改善弹体的自然频率,使弹体快速,稳定的跟踪指令。
2)当系统的闭环极点的阻尼比大于0.5,且实极点小于0时,可保证系统在舵机处有45°以上的相位裕度。
3)当弹体参数不确定时,通过给定期望的极点
域,采用参数空间法设计的驾驶仪可以达到设计要求,具有很好的鲁棒性。
4)采用参数空间法设计驾驶仪的算法简便易行,便于工程应用。

