多尺度形态学的局部对比度增强优化算法*

刘 莉,刘 珊,钱雪飞

(1 北华航天工业学院电子与控制工程学院,河北廊坊 065000;2 北华航天工业学院机电工程学院,河北廊坊 065000; 3 中国石油管道局工程有限公司,河北廊坊 065000)

0 引言

图像增强是数字图像处理的一个重要分支,它能改善人的视觉效果,比如突出图像中目标物体的某些特点、提取目标的特征参数等,这些都有利于对图像中目标的识别、跟踪和理解[1]。图像在形成过程中最常见的一种图像问题是对比度降低,因此,需要对图像进行增强处理,即突出图像中感兴趣的部分,减弱或去除不需要的信息,增加图像的对比度,从而加强有用信息,得到一种更加实用的图像或者便于进行分析处理的图像。

为了提高图像对比度,学者们提出了很多基于图像对比度的增强算法,如全局对比度拉伸算法、直方图均衡化等[2-3],这样的算法可以使图像灰度级的全部动态范围得到充分的利用,但是并不能有效增强某一目标区域的对比度。为此,又有许多专家提出局部对比度增强算法,例如小波理论[4]、局部对比度拉伸[5]、数学形态学[6]等。小波算法可以提取不同尺度上有用的图像特征,但一些图像细节并不能得到有效的增强效果,而且结果图像并不是很清晰;局部对比度拉伸能够改变某个区域的像素灰度值,但这种变换仅仅能够改变局部灰度值的统计数据,而不能区分一块区域上灰度值的连续变化和在一块区域中由于某个特征(明亮或暗淡)存在引起的灰度变化两者之间的区别,使得图像在两类情况下都均衡地拉伸对比度,导致不需要的对比度增强结果;数学形态学,是实现对比度增强的一类重要算子。它利用结构元素收集图像的信息,考察图像各个部分之间的相互关系,从而了解图像的结构特征,进而进行某一区域的对比度增强。仅运用一个结构元素的形态学对比度算子将仅仅能增强对应于所用结构元素尺寸的尺度上的图像特征,并不能使各个尺度大小的区域得到有效增强。为了使目标图像局部区域的对比度增强效果更好,更容易进行目标识别,图像更清晰,文中提出了一种基于多尺度形态学的局部对比度增强优化算法。

1 传统局部对比度增强算法

传统局部对比度增强算法一般采用局部对比度拉伸算法[7],利用局部统计数据,通过在一个预先确定的包围某一像素的邻域上扩大灰度值和灰度均值间的不同,进而改变图像的灰度值,如式(1)所示:

fEn(x,y)=meanl(x,y)+k[f(x,y)-meanl(x,y)]

(1)

(2)

式中λ是一个用户自定义变量。

上面的变换仅利用局部灰度值统计数据对图像中某一区域进行均衡的对比度拉伸,不能区分区域上灰度值的连续变化和区域中由于明亮或暗淡特征存在引起的灰度变化两者之间的区别,使得在期望的平滑区域内产生不需要的对比度强化,以致需要更进一步的抑制图像对比度增强的处理。数学形态学不仅可以增强图像的局部对比度,而且能够处理空间特征存在的局部对比度问题,因此,可采用数学形态学算子来改进式(1)。

2 多尺度形态学的局部对比度增强算法

2.1 算法的提出

2.1.1 多尺度数学形态学算子

文中研究的基础是灰度数学形态学[8-10],其基本算子主要包括四种:腐蚀、膨胀、开运算和闭运算,基本算子如式(3)～式(6)所示。

设f是输入图像,B为结构元素,Df和DB分别是f和B的定义域,则:

1)灰度膨胀

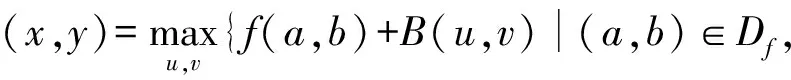
(3)

2)灰度腐蚀

(4)

(3)灰度开运算

(f∘B)(x,y)=(fΘB)⨁B

(5)

(4)灰度闭运算

(f·B)(x,y)=(f⨁B)ΘB

(6)

式中:a=x-u,b=y-v,c=x+u,d=y+v。

在上述基本算子的基础上,Meyer提出了高帽变换算子,包括白高帽变换(WTH)和黑高帽变换(BTH),WTH用来提取明亮图像区域,BTH用来提取暗淡图像区域。定义如式(7)和式(8)所示。

5)白高帽变换

WTH(x,y)=f(x,y)-(f∘B)(x,y)

(7)

6)黑高帽变换

BTH(x,y)=(f·B)(x,y)-f(x,y)

(8)

(9)

(10)

(f∘Bi)(x,y)=(fΘBi)⨁Bi

(11)

(f·Bi)(x,y)=(f⨁Bi)ΘBi

(12)

WTHi(x,y)=f(x,y)-(f∘Bi)(x,y)

(13)

BTHi(x,y)=(f·Bi)(x,y)-f(x,y)

(14)

2.1.2 利用多尺度形态学算子的局部对比度增强

设一幅灰度图像为f(x,y),用灰值形态学算子可表示为:

(15)

式中:(f∘B)(x,y)是灰度图像f(x,y)被灰度值结构元素B(x,y)的开运算。结合式(1)和式(15)可以得到下面的局部对比度拉伸变换:

fEn(x,y)=(f∘B)(x,y)+k[f(x,y)-(f∘B)(x,y)]

(16)

这里k(k>1)依然是一个全局扩大因子,该变换使明亮特征变得更亮,进而提高了局部对比度。现在设k=2。式(16)变为:

fEn(x,y)=f(x,y)+[f(x,y)-(f∘B)(x,y)]

(17)

(18)

(19)

(20)

同理,在多尺度黑高帽变换的基础上以类似的方式处理可以得到暗淡特征的局部对比度拉伸,如式(21)所示:

(21)

将两种特征的局部对比度拉伸公式进行结合,以获得改进图像,将式(20)和式(21)相加除以2得到局部对比度增强公式:

(22)

常系数0.5被用作将明亮和暗淡两种特征分配均等或许以公正的权重。为了推广到更一般的情况,将式(22)改写为:

(23)

这里所有特征,不论暗淡还是明亮,比尺度n小的都假定为图像中的噪声。

2.2 算法的实现

1)形态学塔形的建立

在式(23)的执行中,描述了基于局部对比度增强的特征涉及许多形态学塔形的建立,待增强图像运用高阶相似的圆盘型结构元素进行一连串的灰值形态学开运算操作。图像的结果序列被存入一个塔形中,塔形称作开运算塔形。同理,闭运算塔形是由输入图像的灰度闭运算的一系列结果构成。因此在开运算(闭运算)塔形的第i个条目包含图像被结构元素iB开运算(闭运算)的结果。

2)差别塔形的建立

开运算后图像的像素灰度值小于或者等于原始图像的灰度值,将其分别保存在形态学塔形的相应条目里,将原始图像灰度值与开运算塔形的每个条目分别做差,得出在特定结构元素尺度上的明亮图像特征,并保存在另一塔形的相应条目里,这个塔形叫做差别塔形。同理,另一个差别塔型由闭运算塔形及其相应的暗淡图像特征构成。因此,在对应于开运算(闭运算)的差别塔形的第i个条目包含了小于或者等于iB的明亮(暗淡)特征。

3)重建图像

为了重建最终图像,所需步骤如下:

①将对应于开运算操作的差别塔形的所有条目相加,得到多尺度下的明亮特征组成的结果图像。

(24)

②同理,将对应于闭运算操作的差别塔形的所有条目相加,得到多尺度下的暗淡特征组成的结果图像。

(25)

③将原始图像、多尺度下的明亮特征组成的结果图像和暗淡特征组成的结果图像相结合,得到最终的局部增强图像。

fEn(x,y)=f(x,y)+0.5So(x,y)-0.5Sc(x,y)

(26)

“+”和“-”操作被用于三幅不同图像的对应像素之间。但在一些情况下,用式(26)计算的fEn(x,y)值可能会超过允许的像素灰度级范围。在这种情况下,权值0.5可以替换成μ,从而使少于总像素数1%的点的灰度值被截断,其中,μ的值利用二值搜索技术可以在0到0.5之间选择。

具体算法执行框图如图1所示。

图1 算法执行框图

3 实验结果及分析

3.1 实验结果

为了显示提出算法的效力,选用Walkbridge图像,对其进行增强处理,并用直方图均衡化、基于局部数据的对比度拉伸以及常系数对比度拉伸等不同的方法与之作比较。在实验中,局部窗口被固定成13×13,选用的尺度数为n=6,结构元素B尺寸大小为3×3,常系数局部直方图拉伸算法中扩大因子被固定为5,在利用局部统计数据的局部对比度增强中,扩大因子为0.8。试验在Matlab7.1上运行[11],实验结果如图2所示。

图2中,基于局部数据的对比度拉伸算法一定程度上增强了对比度,但是也产生了一定数量的噪声;而局部直方图均衡化算法的结果有严重的噪声,完全影响了图像的应用;常系数局部对比度拉伸算法增强了图像,噪声较少,但是与提出算法相比,噪声和失真仍然存在,尤其在明亮图像区域上,存在过度增强的情况;而提出的算法可以有效增强图像,生成最少噪声,与原始图像的对比度相比,效果更好。

3.2 实验结果分析

文中选用图像峰值信噪比对实验中的算法作一个定量比较。峰值信噪比是一种评价图像的客观标准,广泛用来检测图像质量,其表示为PSNR,定义如式(27)所示:

(27)

式中:(x,y)是图像像素的坐标,f和fEn分别表示原始图像和增强后的图像。PSNR值越大,表明图像增强算法的性能越好,产生的噪声越少。

通过计算几种局部算法和提出算法的PSNR值,将每种算法的PSNR平均值作比较,如表1所示。从表1中可以看出,提出算法的PSNR值最大,这表明提出算法的图像对比度增强的性能最好,可将其运用在不同的应用中。

图2 Walkbridge图像增强结果

局部数据对比度拉伸局部直方图均衡化常系数局部对比度拉伸提出算法24.40423.73725.59726.732

4 结论

文中提出了多尺度形态学的局部对比度增强优化算法,该方法利用多尺度形态学理论,对传统的局部对比度增强算法进行了改进,通过建立形态学塔形和差别塔型,最后对局部图像进行重建,进而实现图像对比度增强。实验结果表明,同其他局部增强算法相比,提出的算法对图像的局部对比度增强效果最好,产生的噪声最少。通过计算几种算法的峰值信噪比,对几种局部增强算法的效果进行定量比较得知,提出算法对图像局部增强的性能最好。因此,可根据需要,将其应用在不同图像的局部小目标增强和识别中,应用前景广泛。