人工神经网络在导引头去耦中的运用*

李相平,陆志毅

(海军航空工程学院电子信息工程系,山东烟台 264001)

0 引言

导引头是决定导弹命中率的重要部分,主要是对目标的动态信息进行测量,通过机械装置产生制导律从而使天线跟踪目标。在导弹制导的过程中,噪声、天线罩误差以及干扰力矩等因素都会影响导弹的命中率。尤其是干扰力矩,可以说是回路中由于弹体质心不稳以及天线电轴与内部各零件摩擦带来的最复杂的非线性影响因素,并且在导引头跟踪过程中对于干扰力矩十分敏感。所以为了能够提升导弹的性能,对导引头跟踪回路中干扰力矩进行在线补偿,隔离因为干扰力矩带来的弹体扰动与导引头耦合问题是当前需要解决的关键技术问题。文献[1]提出一种前馈补偿的算法对干扰力矩进行补偿,但是只能用于处理简单线性的回路系统,并且需要建立精确的模型,要求较高;文献[2-3]从传递函数的角度上分析了线性化干扰力矩对导引头视线角速率提取的影响,没有给出具体的解决方案;文献[4-5]论述了简化后的弹簧力矩和阻尼力矩对导引头性能的影响;文献[6-7]研究了在存在雷达信号噪声的情况下导引头干扰力矩引起的隔离度问题,表明有噪声时会增大隔离度对导弹脱靶量的影响。因此,由于干扰力矩存在带来的隔离度问题不仅对导引头输出视线角速率的精度产生影响,还会恶化整个控制跟踪回路的稳定性,降低导弹的命中精度。文中提出了一种基于神经网络的前馈补偿算法,通过对干扰力矩进行实时监督,进行自适应前馈控制,有效地解决保证输出的信号误差最小,较好地提升了导弹的性能。

1 干扰力矩模型的建立

1.1 质量不平衡引起的干扰力矩

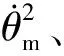
mr0cos(θl-θh-θm-θ0)am

(1)

式中:m是导引头的质量;θh是天线电轴与弹体中心线的偏离角;θm是弹体角;θl是导弹攻角;r1是弹体重心和天线电轴之间的距离;am是导弹横向加速度。

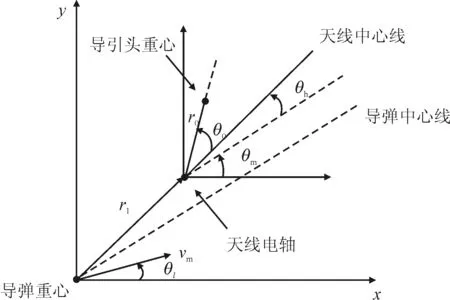
图1 导弹的几何构型图

补偿距离r0对导弹的性能影响很显著,尤其是对导弹脱靶量。图2表示导弹脱靶量的均方根与r0的变化曲线。可以看到,即使很小的r0也会造成很大的脱靶量。

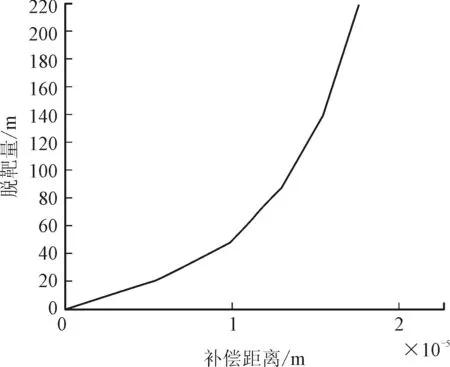
图2 质量不平衡对导弹脱靶量的影响

1.2 天线电轴摩擦引起的干扰力矩

由于导引头构造复杂,其内部零件众多,因此带来的摩擦是非线性的,这里主要讨论天线电轴摩擦引起的干扰力矩,其表达式为:

(2)

其对应的变化曲线如图3所示。

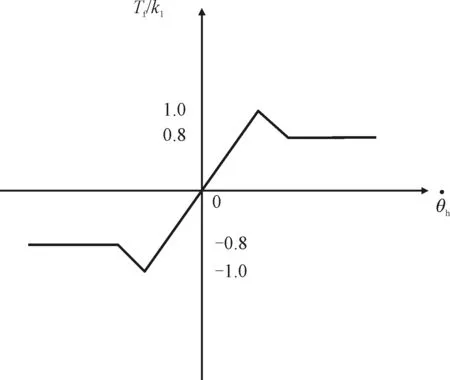
图3 摩擦力矩表达式示意图

为了表示摩擦引起的干扰力矩对导弹性能的影响,将导弹脱靶量随摩擦系数k1变化的曲线图引入,如图4所示。

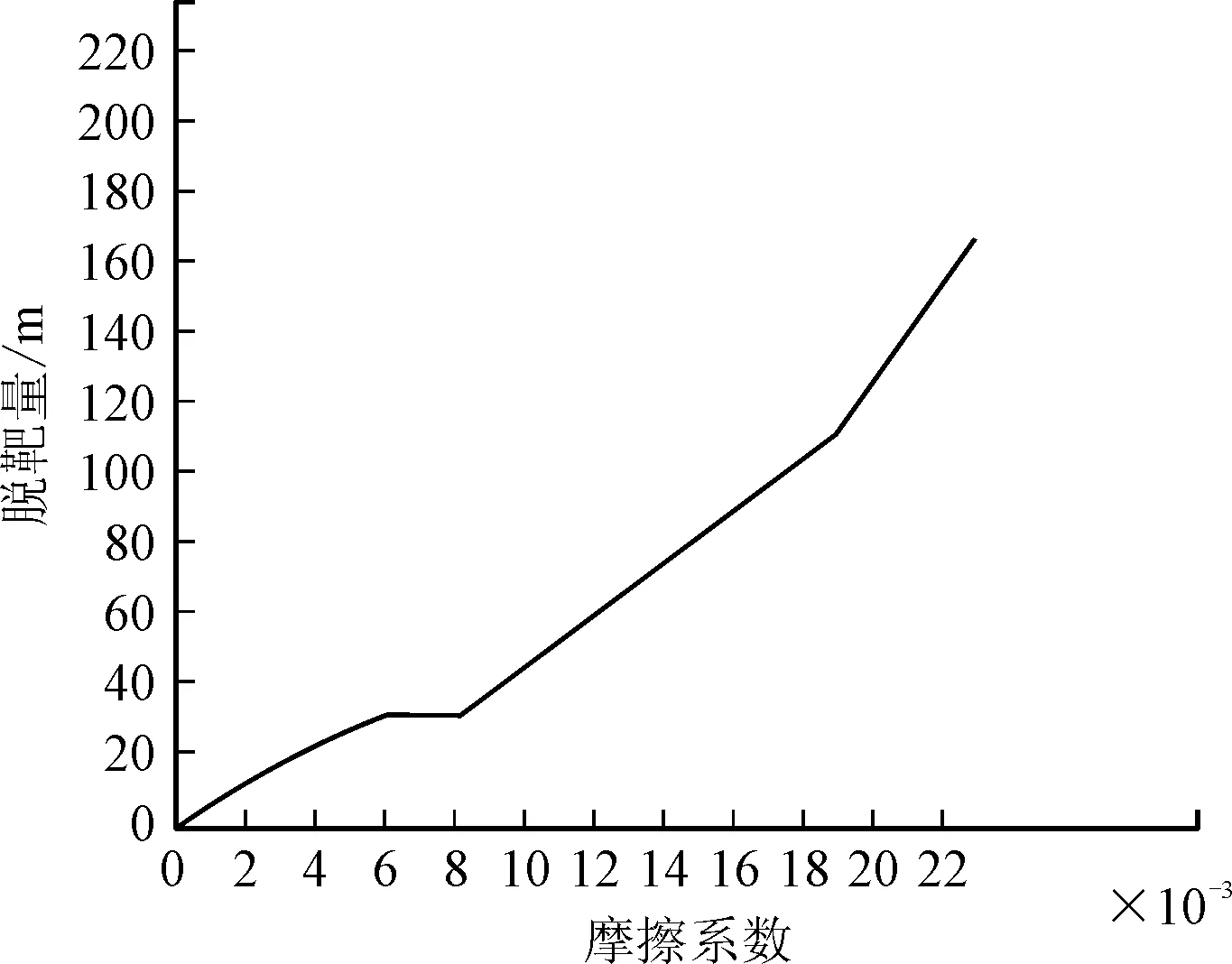
图4 摩擦系数对脱靶量的影响曲线图

那么对于整个导引头跟踪控制回路来说,其因为导弹质量不平衡和天线电轴摩擦带来的系统干扰力矩为Td=Tm+Tf,为了隔离系统干扰力矩对导弹性能的影响,必须要对干扰力矩进行在线补偿。

2 神经网络补偿的原理

为了解决导引头干扰力矩引起的隔离度问题,可以采用多层感知器神经网络进行力矩补偿。多层感知器网络有较强的分类能力,能够处理非线性的问题,主要包括输入层、隐含层和输出层,其中隐含层可以是一层或多层,可以完成较复杂的任务。对于多层感知器中的每个神经元来说,激活函数通常取可微的函数,比如sigmoid函数:

(3)

式中:ui是第i个神经元的输入信号;vi表示第i个神经元的输出信号。

2.1 生物神经元的结构

人工神经网络实际上是从生物神经网络发展而来的,对于一个人而言,在大脑皮层大约有100亿个神经元,60万亿个神经突触以及它们的连接体[9]。人的大脑在学习的过程就是神经元之间连接强弱程度变化的过程,最终对信息的处理也是综合神经元细胞的整体状态来确定的。

具体的,每个神经元是由细胞体、树突、轴突以及突触组成。细胞体是神经元的主体部分,是给神经元提供能量的重要场所;树突则是由细胞体向外界延伸的神经纤维,这些神经纤维有许多突起,可以通过它们来接收来自其他神经元的信息;轴突则是向外延伸最长的神经纤维分支,相当于输入端口,主要是传出神经冲动[10];突触是神经元之间进行通信的接口。经过现代的生理学研究表明,大脑的活动并不是通过多个生物神经功能简单叠加完成的,而是许多神经单元非线性的动态处理。所以,由此转化而来的人工神经网络可以较好地处理一些非线性问题,可以用于导引头干扰力矩的补偿和去耦。

2.2 神经网络的学习算法

针对影响干扰力矩的因素,可以通过多感知器的神经网络不断进行学习和训练,最终使得干扰力矩得到补偿,保证输出的信号误差最小,其算法原理框图如图5所示。

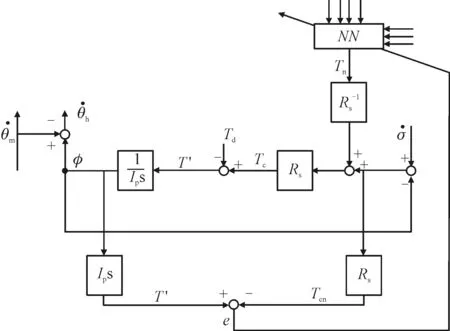
图5 导引头神经网络补偿算法原理框图

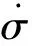
在该模型中误差函数为:

(4)

对于神经网络的输入和输出,可以用下式表示两者之间的关系:

netj=Wjzj-1

zj=fj(netj),j=1,2,3,…,N

(5)

式中：fj(·),j=1,2,3,…,N是选取的激活函数,这里取sigmoid函数；zj-1和zj分别是神经元的输入和输出信号；Wj是每个神经元的连接权重。

对于感知器各层之间的权重,可以用BP算法进行学习,其详细的学习过程如下:

1)隐含层第二层和输出层之间权重U的学习为:

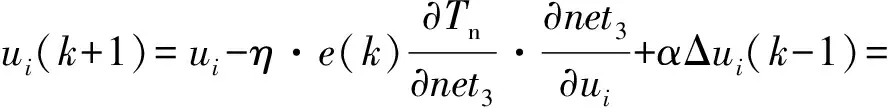
(6)

式中:

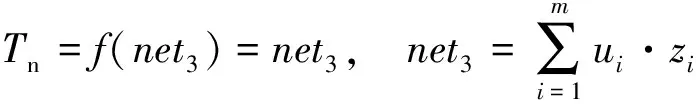
式中：关于net2i的定义在式(7)中有说明。

2)隐含层之间的权重V的学习为:

vij(k+1)=vij(k)-η·e(k)·ui(k)·f′(net2i)·

yj(k)+αΔvij(k-1)

(7)

式中:

yj=f(net1j),i=1,2,3,…,m;j=1,2,3,…,n

3)输入层和隐含层第一层之间权重W的学习为:

f′(net1i)·aj+αΔωij(k-1)

(8)

式中:

i=1,2,3,…,n;j=1,2,3,…,7;l=1,2,3,…,m

3 仿真结果与性能分析

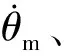
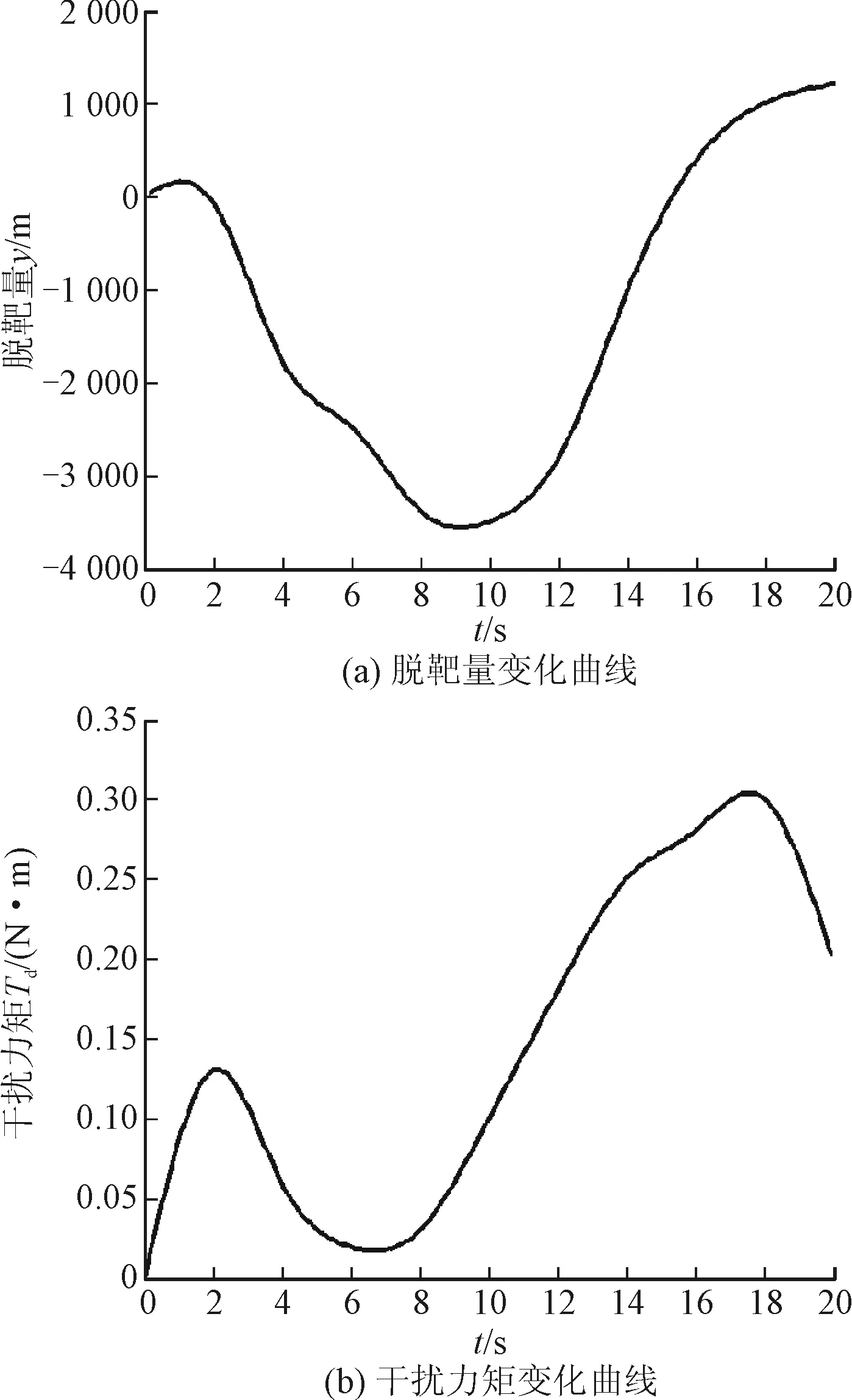
图6 未补偿系统的脱靶量和干扰力矩的曲线图

通过设计的感知器神经网络不断进行学习和训练,对补偿后的导弹脱靶量和干扰力矩进行仿真实验,其结果如图7所示。

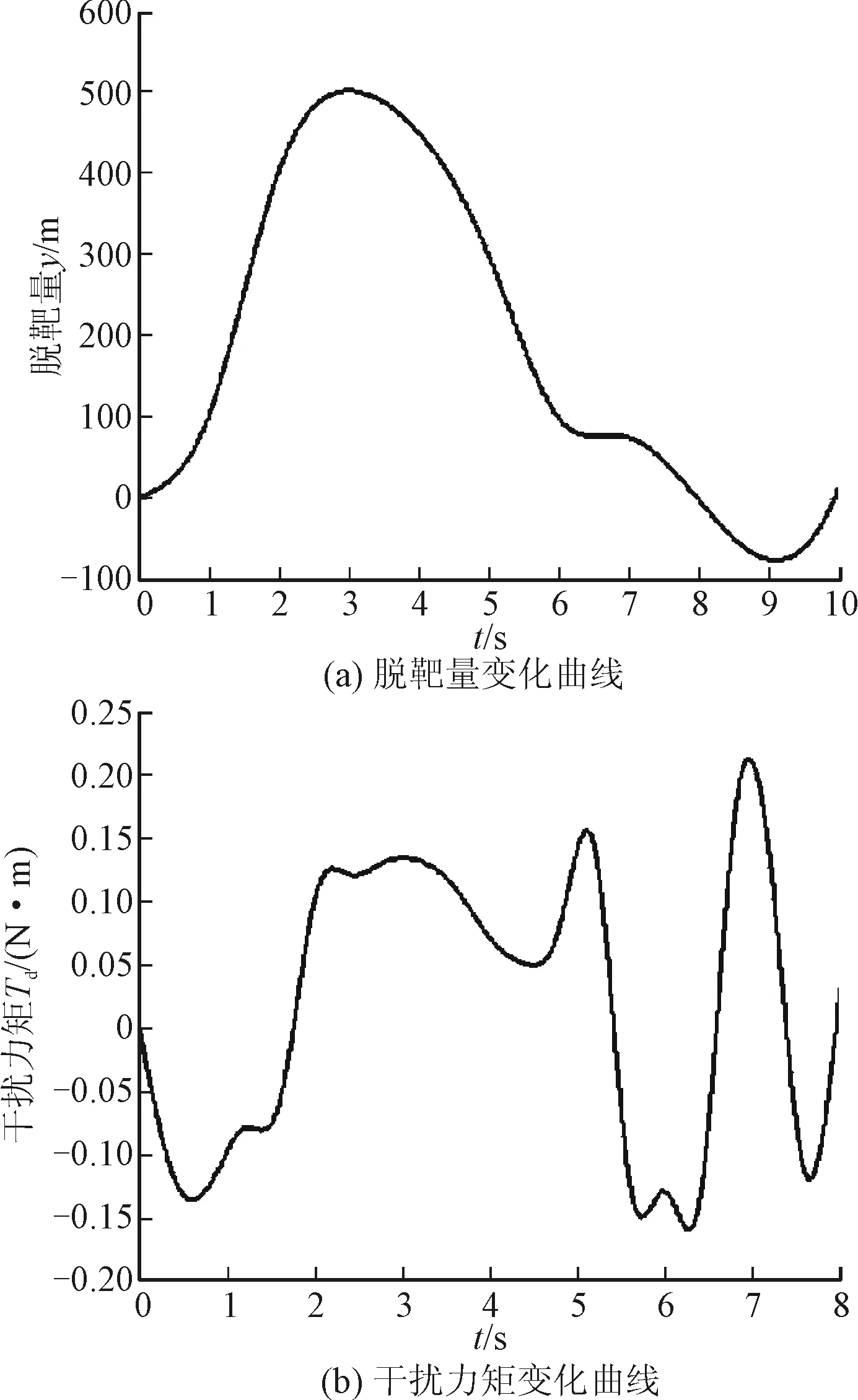
图7 补偿后系统的脱靶量和干扰力矩的曲线图

通过仿真结果发现,未进行补偿前导弹的脱靶量受干扰力矩的影响十分明显,并且脱靶量的范围很大,极大程度上降低了导弹的性能。通过文中设计的感知器神经网络进行干扰力矩的前馈补偿后,脱靶量有了很大程度的改善,表明应用多感知器神经网络算法减小了系统干扰力矩的影响,一定程度上降低了因为干扰力矩带来的耦合问题,提高了导弹的命中精度。

4 结论

由于多感知器神经网络对非线性问题有很好的适应性,可以很好地模拟各个因素之间的变化情况,也不需要很多先验知识和精确的模型,使问题处理起来更方便。同时在感知器输入层、隐含层和输出层之间权重的不断训练的过程中,参数得到改善,使得输出的误差减小。

通过设计多感知器的神经网络模型处理导引头干扰力矩问题,对导引头产生干扰力矩的因素反复进行学习和训练,产生与系统干扰力矩相近的力矩进行补偿,达到了较好的效果,也表明神经网络在导引头去耦问题上的有效性和可行性。