空地导弹数据链干扰效能仿真与优化研究*

龚 燕,刘雅奇,李 健

(国防科技大学电子对抗学院,合肥 230037)

0 引言

导弹数据链是指安装在导弹及飞机、卫星、等平台上,实现导弹状态、战场态势、控制指令等信息双向传递的数据通信系统[1]。以数据链技术为支撑,现代战术导弹能够完成“目标选择与重瞄”、“战场杀伤效果评估”等多重任务[2]。而采用通信对抗手段对敌导弹数据链进行干扰,破坏其各类作战信息的传输,将能够有效降低敌导弹的命中精度,削弱其作战效能。

目前,已有不少文献对数据链的对抗技术进行了研究,例如:针对通用数据链,文献[3]讨论了跳频干扰和直接序列扩频干扰两种对抗技术;针对Link16数据链,文献[4]提出了对其消息同步段实施干扰对抗;针对Link11数据链,文献[5]研究了同步音干扰等干扰的效能,等。而对战术导弹数据链对抗的研究却十分少见,仅文献[6]针对某型空地导弹数据链设想了一种侦干一体对抗设备的技术方案,并对其战术使用方式做了简要讨论。在此基础上,文中尝试对典型空地导弹数据链的干扰过程进行建模仿真,进而对其作战使用做简要讨论。

1 机动模型

目前,公开文献中常见的导弹数据链主要有AN/AXQ-14、AN/AWW-13、Link-16等[7-9]。从通信技术上来看,导弹数据链与其他数据链相比,导弹的高速机动造成的通信环境快速变化是导弹数据链的本质特征。因此,对导弹及战斗机的运动建模是空地导弹数据链干扰仿真的基础内容。

六自由度建模方法[10]能够对导弹和战斗机的质心移动和转动做出详细的刻画,但它需要以大量如空气动力系数、导弹或战斗机气动外形等不易获得的模型参数为支撑,因此文中决定通过对战斗机和导弹机动过程的分析,给出一种简化的机动建模方法。

1.1 战斗机机动模型

根据文献[11],战斗机在空战中常用7种常规机动方式:最大加速平飞;最大减速平飞;最大过载爬升;最大过载俯冲;最大过载左转;最大过载右转;稳定飞行。因此,对战斗机机动过程可通过指定战斗机的机动性能和各阶段的机动参数进行模拟。表1详细列举了这些模型参数:

表1 战斗机机动模型参数

表1中:

1)最大加速度包括:加速平飞加速度a1、减速平飞加速度a2、爬升转向加速度a3、俯冲转向加速度a4和水平转弯加速度a5。

2)速度极值包括:最大和最小平飞速度v1、v2。

3)机动方式参数应取值于前述7种常见机动方式,其中,当选择最大过载爬升或最大过载俯冲方式时,还应指定爬升或俯冲的角度φ1、φ2。

4)机动阶段的结束可有时间、速度、高度和角度四种触发条件。其中,时间条件是指阶段在指定时间Tend结束;速度条件是指平飞速度达到指定值Vend时阶段结束;高度条件是指战斗机的位置达到指定高度Hend时,爬升或俯冲结束;角度条件是指战斗机的速度方向达到指定角度θend时,转弯机动结束。

匀加速直线飞行(包括最大加速平飞、最大减速平飞和稳定飞行)的机动轨迹按下式计算:

(1)

最大过载爬升/俯冲的机动过程分为三个阶段,一是改变速度倾角的匀速圆周运动,其运动轨迹按式(2)计算;二是定倾角的爬升或俯冲运动,其轨迹按式(1)计算;三是恢复平飞状态,该过程是第一阶段的逆过程,其运动轨迹仍按式(2)计算。

(2)

最大过载转弯的机动轨迹按式(3)计算:

(3)

式中：S和v分别为战斗机的位置矢量和速度矢量;φ表示瞬时俯仰角;θ表示瞬时水平方向角,按式(4)计算;带有上标“′”的变量表示这些变量在下一仿真步长的取值;a表示平飞、爬升或俯冲、转弯的过载加速度;ΔT表示仿真步长。

(4)

1.2 导弹机动模型

根据文献[12],空地导弹的飞行轨迹可分为抛撒段、下滑段、平飞段和俯冲段四个阶段。表2列出了空地导弹的机动模型参数。

表2 空地导弹机动模型参数

抛撒段的运动轨迹按式(5)计算,其中g表示重力加速度:

(5)

下滑段的运动轨迹与战斗机俯冲的过程类似,也可将其分成3个阶段,分别用式(2)、式(1)、式(2)计算。平飞段可分为向目标转向、匀加速直线运动和匀速直线运动三个阶段,分别可用式(3)和式(1)计算。俯冲段可分为两个俯冲转向和加速直线俯冲两个阶段,其中俯冲转向段的机动轨迹可按式(2)计算;加速直线俯冲段按式(1)计算。

2 数据链干扰模型

文献[12-13]列举了数据链通信在若干种常见干扰样式下的误码率计算公式,例如在正态白噪声干扰,相干解调的条件下,2ASK、2FSK、2PSK的误码率分别为:

(6)

(7)

(8)

可见,对多数通信样式来说,信噪比SNR对误码率Pe都起到了重要的决定作用,且一般SNR越大,Pe越小。基于以上考虑,文中不再具体讨论某一种通信样式或干扰样式,而仅对机动条件下数据链接收端的信噪比进行分析。

设战斗机和导弹上搭载的数据链终端的发射功率和天线主瓣增益分别为Pa、Pm和Ga、Gm,干扰机的发射功率和天线主瓣增益分别为PJ和GJ,考虑自由空间传播的简化情况,则机载数据链的通信信号接收功率为:

(9)

式中:Ram表示导弹和战斗机之间的距离,可通过第2节的导弹机动轨道模型求出;λ表示信号波长。对应的干扰信号接收功率为:

(10)

式中:RaJ表示干扰机与战斗机之间的距离;ηJ表示对机载和弹载数据链的干扰损耗率;Ga(θa)表示机载数据链天线在干扰机方向的天线增益;θa表示干扰机方向相对机载数据链天线主瓣方向的夹角。

则机载的接收信噪比为:

(11)

同理,可得弹载数据链的接收信干比为:

(12)

式中：KTΔfF表示数据链接收设备的内部噪声,它可看作是仅与电子设备技术性能有关的常数。

根据文献[9],现代导弹数据链广泛采用天线波束控制和自适应调零技术,它能够将天线波束汇聚成很窄的针状,并根据战斗机或导弹的飞行状态,实时将波束对准通信目标。对此,我们将天线增益简化为式(13)所示模型:

(13)

而干扰机方向与机载或弹载数据链天线主瓣方向的夹角可按下式计算:

(14)

(15)

3 仿真实例

3.1 机动仿真

令战斗机的初始位置为(0,0,5 000 m),初速度为(800 km/h,0,0),地面目标的位置为(50 km,50 km,0)。0 s时,战斗机发射一枚空地导弹,其机动模型参数如下:抛撒段持续10 s;俯冲倾角为-30°,俯冲结束高度为1 000 m,俯冲转向加速度为100 m/s2,爬升转向加速度为50 m/s2,水平转弯加速度为2 m/s2,水平直线加速度为30 m/s2,俯冲攻击距离为5 km。战斗机的机动过程为:导弹发射后,继续稳定平飞30 s;然后向目标方向转弯;再向目标方向稳定平飞10 s;接着,以-20°倾角俯冲下降到4 000 m高度;再向目标方向稳定平飞15 s;然后,左转弯到与初速相反的方向,即-90°;最后沿该方向稳定平飞至仿真结束。战斗机的性能参数如下:俯冲转向加速度为10 m/s2,爬升转向加速度为5 m/s2,水平转弯加速度为10 m/s2。则战斗机与导弹的机动仿真结果如图1所示。

3.2 数据链干扰仿真

图1 空地导弹与战斗机的机动轨迹仿真

假设使干扰有效的信噪比门限为SNRmin=10 dB,则由图可见,在第198 s干扰机对机载数据链达成有效干扰,而对弹载数据链,则需在第225 s后才能干扰有效,虽然机载终端发射功率相较弹载终端更大,但也距地面更远,在自由空间波传播损耗下,机载终端的信噪比始终小于弹载终端。图2(a)中,信噪比在197 s时有个跳变,这主要是因为随着导弹逐渐接近目标,干扰信号开始进入机载数据链的天线主瓣;图2(b)中,200 s后信噪比以越来越大的斜率加速减小,这主要是因为随着导弹接近目标,弹载数据链接收到的干扰功率急剧增加。对比图2(a)、图2(b)可见,在本例情况下,为了尽早达成对导弹数据链的有效干扰,应以导弹发射平台战斗机为主要干扰目标。

3.3 配置位置优化

图3给出了一个直观形象的空地导弹数据链干扰示意图。由图可见,通过合理选择干扰机的配置位置,可使干扰波束进入数据链天线主瓣波束的时间提前。显然,有效干扰的总时间越长,对其空地攻击的破坏效果也就越大。

图3 空地导弹数据链干扰原理示意图

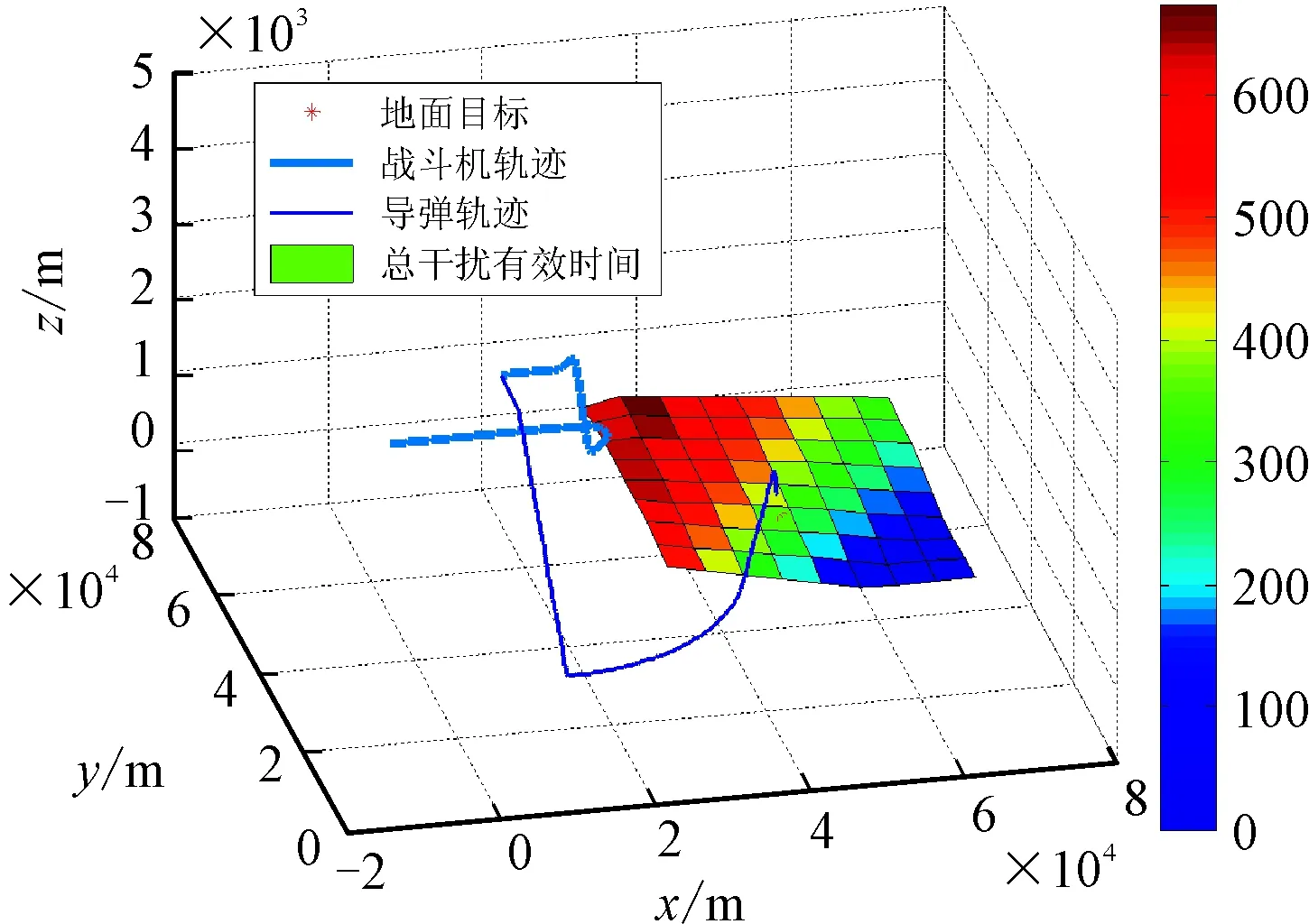
图4 总有效干扰时间与干扰机配置位置的关系

对此,我们以总有效干扰时间T为效能指标,对保卫目标周边40 km×40 km的区域以5 km为步长做均匀采样仿真,结果如图4所示。

由此可见,将干扰机配置在(35 km,65 km,0)位置处能够取得最大的总有效干扰时间;而从总体上看,将干扰机配置在保卫目标的西北方位能够取得更好的干扰效果。

4 结论

导弹的高速机动造成的通信环境急剧变化是导弹数据链与卫星、舰船等其他平台数据链的主要区别。对此,文中将导弹机动和数据链干扰的仿真结合了起来,仿真结果能够直观显示干扰效果在整个作战过程中的动态变化。通过仿真实例可以看出,相比弹载终端,对机载终端的干扰往往能够取得更大的总有效干扰时间。

文中的研究重点主要在于将机动仿真与干扰仿真结合起来,但所建立的模型都是理想化的简化模型。当考虑更细致的实体运动姿态以及干扰信号样式特征时,则需对这些仿真模型做进一步的深入细化,这将在下一步研究中继续展开。