对《一个有趣的数学猜想及证明》一文的补充

蒋金团

（云南省保山市施甸县第一完全中学，云南 保山）

笔者曾发表过《一个有趣的数学猜想及证明》文章，某读者看过后，觉得文中“用反证法证明猜想”这一段抽象难懂，所以很有必要对该文章进行完善和补充。如下面表格所示，将自然数分成十行，每一行都是公差为10的等差数列，第一行的通项公式为10k1+1（k1=0、1、2、3…），第九行的通项公式为 10k9+9（k9=0、1、2、3…），第十行的通项公式为 10k10+10（k10=0、1、2、3…）

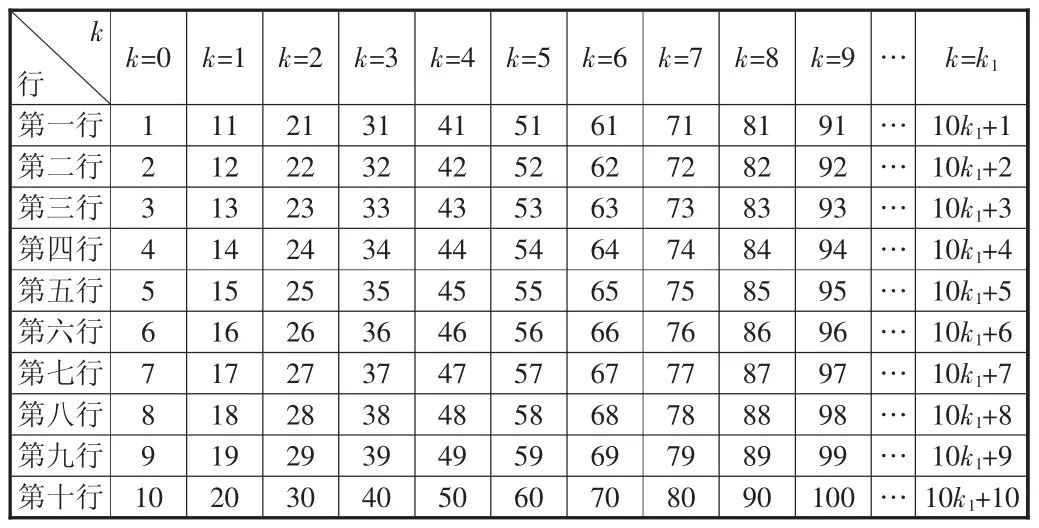
一、讨论变换特点

根据变换规则，对奇数实行“乘3加1”变换之后将变为偶数，具体如下，第1行奇数将演变为第4行偶数，第3行奇数将演变为第10行偶数，第5行奇数将演变为第6行偶数，第7行奇数将演变为第2行偶数，第9行奇数将演变为第8行偶数。

根据变换规则，对偶数实行“除以2变换”变换，相应的约束关系讨论如下。

1.第2行偶数的变换特点

对第2行偶数实行“除以2”变换之后，有一半偶数转变为第1行奇数，另一半偶数转变为第6行偶数，相应的约束条件如下：

（1）第 2行（10k2+2）除以 2转变为第 1行（10k1+1）时，有=10k1+1，即约束条件为，为保证k为整数，k只能12取偶数，即 k1=0、2、4、6、8、10…，对应的 k1值为 k2=0、1、2、3、4、5…

上述讨论结果可用如下流程图表示：

（2）第2行（10k2+2）转变为第6行（10k6+6）

上述讨论结果可用如下流程图表示：

同理可讨论其他行偶数除以2之后的变换特点和上述流程类似，最后可把各行变换组成如下网状结构。

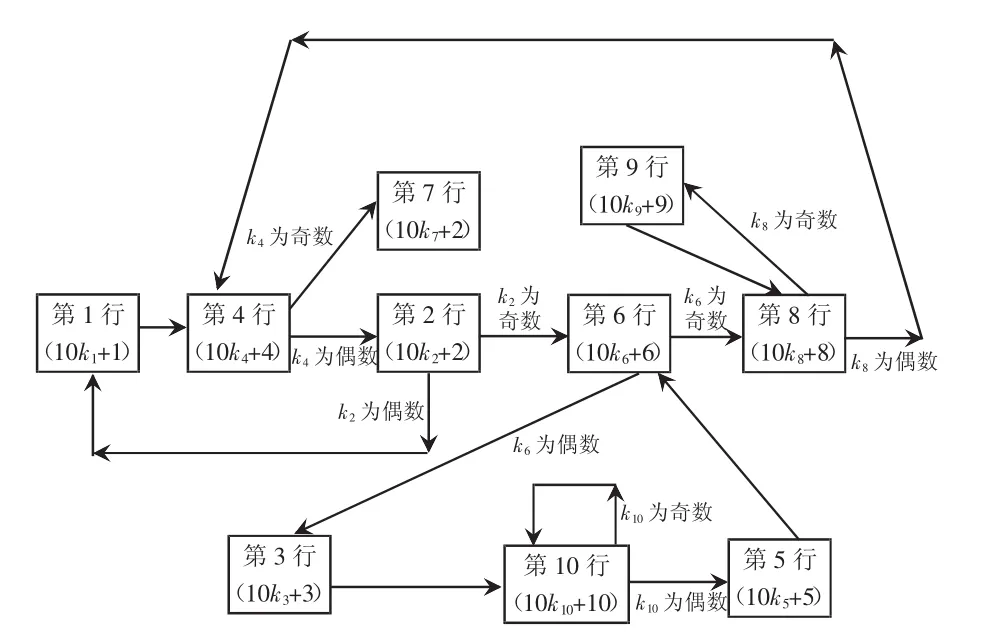
通过以上的网状图可以得出一个重要结论：当自然数从某行演变为另外一行时，每碰到“除以2”变换一次，符合条件的值都会在原来的基础之上减半，因为碰到“除以2”变换时，值将会分成奇偶两支。

2.为了通俗理解，我们可以举个例子，假设第6行数值按如下流程变换：

（1）设第6行数值的通项公式为10k6+6，此时的k6取一切自然数，k6=0、1、2、3、4、5、6…

（2）第6行的数值，有哪些能转化为第3行（10k3+3）的数值？

（3）第3行的数值，有哪些能为第5行（10k5+5）的数值？

二、用反证法证明猜想

假设某个自然数按规则变换后没有要落入“4-2-1-4”循环，则该数将无限度地变换下去，因为除1、2、4外的自然数都不可能回到自身，这样一来，将会遇到无穷次“除以2”变换，无论该数从哪一行开始，每碰到“除以2”变换一次，符合条件的k值都会在原来的基础之上减半，k值最终只能取一个值，即变换最终在同一列之间进行，根据网状图可知，没有落入“4-2-1-4”循环的数将会多次经过第6行，因为最终只剩一列k值了，这说明第6行的某个数值将会回到自身，这与文献1的结论是矛盾的，所以假设是错误的，猜想是正确的。