基于似然比统计量的超高维特征筛选研究

来 鹏，孙 鑫，高羽飞，赵英序

（南京信息工程大学 数学与统计学院，南京 210044）

0 引言

随着网络与通信技术的飞速发展，人们常会遇到各种超高维复杂数据问题，如证券市场的交易数据、X射线断层摄影数据、生物基因表达数据、文档词频数据等。在分析超高维数据问题时，最大的难点是随着维数的膨胀，分析和处理数据的复杂度、成本以及所需的空间样本数都将呈指数级增长。传统的多元统计方法在处理超高维数据问题时会遇到如计算效率无法满足、计算存储空间需求变高、传统统计指标不再适用、方法的假设条件不再满足等困难，所以构建适用于超高维数据的新统计方法是很有必要的。

特征筛选是目前最常见的处理超高维数据问题的手段之一，一般遵循“两步走”的筛选过程：第一步在稀疏性假设下对超高维数据进行大规模粗略的变量筛选，将超高维数据降到一个小得多的低维空间中；第二步再用传统的统计方法进行建模分析。由此可见，初步特征筛选的准确降维直接影响到后续建模。Fan和Lv[1]、Fan等[2]、Fan和Song[3]、Fan等[4]、Liu等[5]在参数或半参数模型下提出了多种特征筛选方法。然而在超高维数据分析过程中，想要找到合适的模型是很困难的，因此，Li等[6]、He等[7]、Mai和Zou[8]提出了无模型下基于多种统计度量指标的特征筛选方法。

在超高维数据分析中，有一类特殊的超高维数据类型，其响应变量和协变量都为分类变量。对于该类问题，Huang等[9]提出了超高维分类数据的特征筛选方法Pearson卡方检验算法（PC-SIS），对超高维数据，利用χ2统计量检验协变量与响应变量是否具有显著的相关关系，即对指标进行排序。

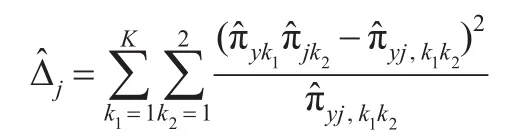
尽管PC-SIS方法拥有很多优点，但其不足也显而易见：Pearson卡方检验要求样本量大于40，样本量越大，得到的效果越好。然而实际情况中这些条件可能无法确保满足，为了对其改进，本文提出了似然比统计筛选方法（LR-SIS）。与PC-SIS相比，似然比统计量是反映灵敏度和特异度的复合指标，不仅非常稳定，而且可用于有20%以上的单元格的期望频数小于5或者最小为1的样本数据。此外，LR-SIS也是一种无模型算法，通过适当分组变换可应用于连续型变量的分组筛选问题。下文将给出LR-SIS特征筛选过程和渐近理论性质，并通过蒙特卡罗数值模拟和实例分析进行有限样本研究。

1 似然比特征筛选（LR-SIS）

超高维数据中，变量维数p远大于样本量n，通常只有少数的协变量与Y有关，满足稀疏性假设。令Y∈{1，2，…，R} 表 示 具 有R类 的 离 散 分 类 变 量 ，X=(X1，X2，…，Xp)T∈Rp表示p维离散协变量，其中Xi可取值为{1，2，…，K}，i=1，…，p。超高维特征筛选关键在于通过分析协变量与响应变量之间的边际相关性，来筛选出可能的重要协变量进行快速降维。为此，令F(y|X)为Y关于X的条件分布函数，定义重要变量集合与不重要变量集合分别为：

其中φy为Y的取值范围。则变量筛选的目的，就是找到一个估计̂使得D⊆̂且||尽可能小，其中||表示集合̂中的元素个数。

为了改进Huang等[9]所提出PC-SIS方法，本文提出了更稳健的似然比统计量作为特征筛选指标。定义，则似然比统计量可定义为：

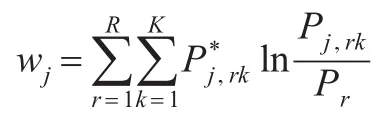
若Xj与Y独立，则P(Y=r|Xj=k)=P(Y=r)，那么ln(Pj，rk/Pr)=0，即wj=0。若响应变量Y与协变量Xj不独立，则存在某些r∈{1，2，…，R}使P(Y=r|Xj=k)≠P(Y=r)，即 ln(Pj，rk/Pr)≠0 ，从而wj≠0 。所以|wj|越大说明Xj与Y相关性越强，因此可以利用|wj|的值评估Xj的重要性。

利用随机样本{Yi，Xi=(Xi1，Xi2，…，Xip)T}，i=1，2，…，n，可求出wj的估计为：

接下来探讨所提出特征筛选方法的理论性质。为方便后续的证明，给出以下条件：

（C1）存在两正数 0＜c1＜c2＜1，使的c1＜Pr，Pj，rk＜c2，1≤j≤p，1≤r≤R，1≤k≤K。

（C2）存在正数，使得 min∈Dj|wj|≥2cn-τ。

（C3）假设lnp≤na，0＜a＜1-2τ。

条件（C1）要求每个类别的响应变量和协变量取值的概率都是有界的，因此排除了那些可能具有特定分类概率过大或过小的取值情况。条件（C2）要求所有重要变量的指标最小值有下界，并随样本量趋向于无穷大时以n-τ的速度趋向于0，在Fan和Lv[1]的文章中也有相似的假设。条件（C3）允许特征维度p随样本量n呈指数级发散，表明了其超高维特性。

定理1（确定筛选性）：在条件（C1）至条件（C3）下，对于任意，有：

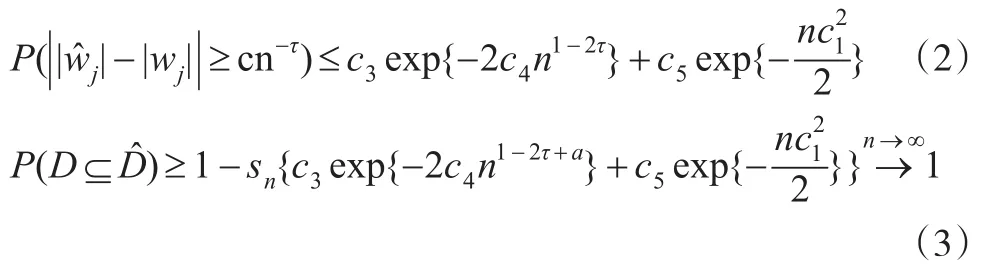
其中c3-c5为正数，sn为D的基数。

2 数值模拟

为了研究所提出似然比特征筛选方法LR-SIS的有限样本性质，本文将利用蒙特卡洛模拟，参考Ni和Fang[10]的例 1 对 LR-SIS 方法与 SIS[1]、PC-SIS[9]、IG[10]、KF[8]等方法进行比较。首先生成Yi∈{1，2，…，K}其中K=2，同时对于任意1≤k≤K，P(Yi=k)=1/k。同时生成二元协变量向量X={X1，X2，…，Xn} ，其中Xi={Xi1，Xi2，…，Xip}T，定义真实的重要变量集为D={1，…，10}，|D|=d0。在Yi的条件下，生成Xij满足P(Xij=1|Yi=k)=θkj，1≤k≤K且j∈D，详细数值见表1。其次，对于1≤k≤K且j∉D，本文定义θkj=0.5。设协变量的维度p=2000，样本量n=160，240，320。

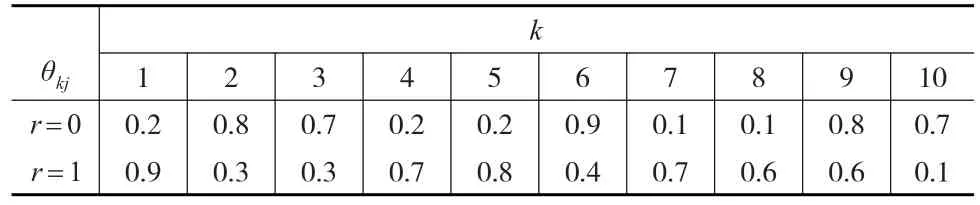
表1 模拟所用参数规格

为了便于比较，仿照Ni和Fang[10]，定义下列结果评估标准：MMS，包含所有重要变量的最小模型尺寸；P，在给定模型尺寸为[n/logn]的情况下是否包含所有重要变量的指标；MS，模型尺寸d，由Ni和Fang[10]中所提出的d值算法所得的筛选变量个数，其中dmin=1，dmax=n；dc表示被正确挑选出的重要变量的数量；di=d-dc表示被挑选出的不重要变量的数量；CZ，在所有p-d0个不重要变量中，没有被挑选出的不重要变量所占的比例；IZ，在所有d0个重要变量中，没有被正确筛选出的重要变量所占的比例；CP1，表明所选出的模型包含所有的重要变量的比率；CP2=dcd0，表示所筛选出的重要变量占所有重要变量的比率。

表2记录了500次模拟中MMS的5%、25%、50%、75%和95%的分位数值以及其他评价指标的平均值。从表2中可以看到当样本量和维数相同时，LR-SIS方法的效果最好，MMS中每个指标都接近10，说明LR-SIS能够更有效地筛选出所有重要的协变量；IG方法仅次于LR-SIS，与其他方法相比，其优越性主要体现在筛选重要协变量的错误率更低，PC-SIS与SIS效果近似，他们的优势在于具有较好的MMS指标；KF方法的MMS结果比较差，但其筛选重要协变量的正确率更高。随着样本量n的不断增大，LR-SIS方法在各指标的收敛速度最快，与其他方法相比更加稳定，计算效率较高。因此可见LR-SIS方法具有较显著的优越性。

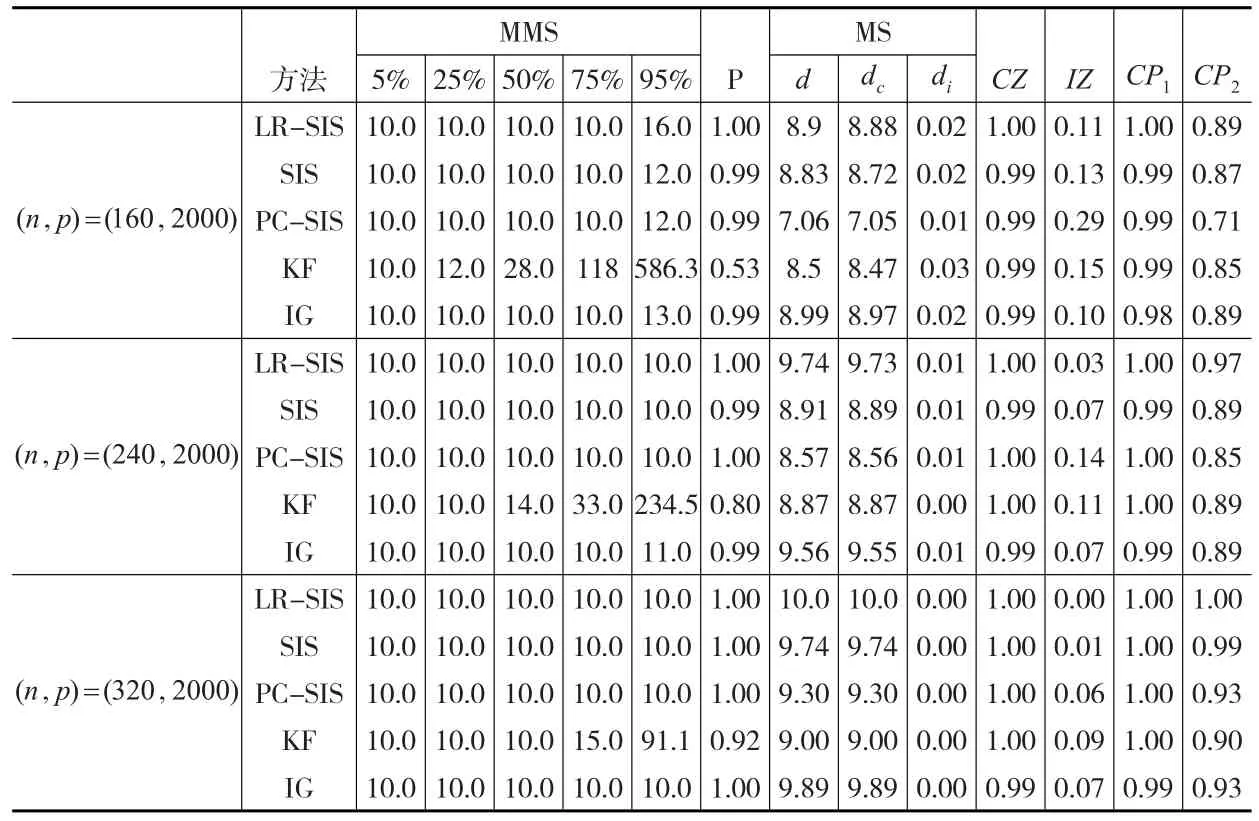
表2 模拟结果

3 实例分析

在研究文本分类问题的过程当中，特征筛选是最重要的环节之一，能够降低特征向量空间维数，简化计算。本文从UCI机器学习库收集到亚马逊网站关于电影的大量评论（http://archive.ics.uci.edu/ml/datasets/Sentiment+Labelled+Sentences#）。该评论集中包含正面评论(Y=1)和负面评论(Y=0)（部分评价如表3所示）。则所要研究的问题为利用评论中出现来源于词库的关键词X=(X1，…，Xp)T，来预测评论的类别Y，这是一个超高维文本分类问题。

表3 亚马逊电影评论文本

经过数据整理，利用LR-SIS方法对此评论集进行关键词筛选。表4根据ωj值对影响评价分类的关键词进行了排序。从这些排名靠前的关键词可以看出，评论者主要从电影本身、演员、演技以及音乐等方面对电影进行评价，重点关注这些方面的质量、好坏、趣味性等，来对电影做出正面或负面的评价。

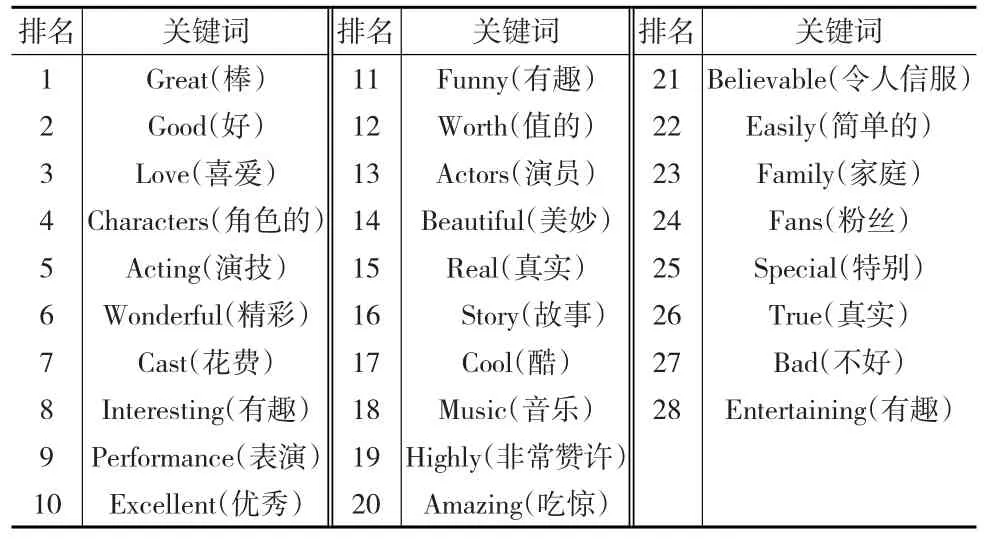
表4 电影评价分类与关键词筛选结果

通过LR-SIS方法进行特征筛选后，利用决策树模型进行判别分类，对整个数据集270条负面评论、240条正面评论进行判别的分类结果见表5。可以发现总共510条评论，LR-SIS结合决策树的错判率为0.126。错判率比较低，说明LR-SIS方法的筛选效果不错，利用LR-SIS方法来进行降维和判断评论的正负性是合理可行的。

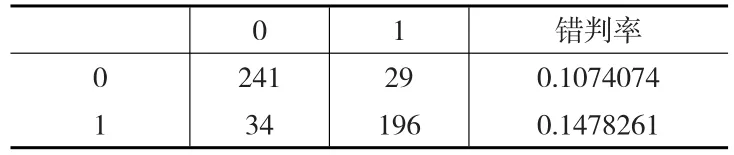
表5 LR-SIS方法预测结果

4 定理证明

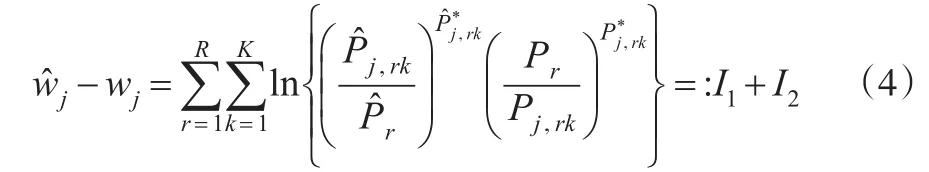
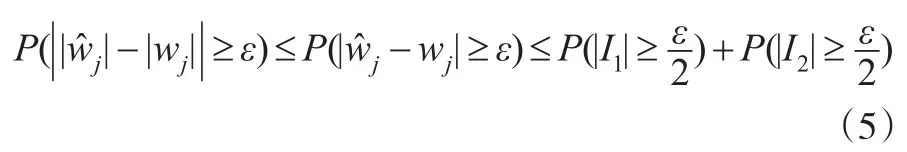
因此有：I1与I2拥有相同的结构，下面只处理

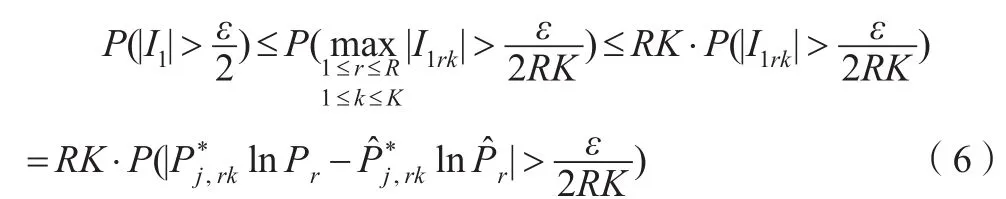
由Hoeffding不等式：

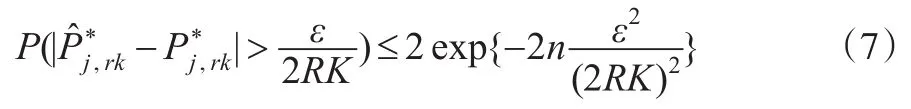
通过积分中值定理，知在Pr与间存在使得。 当时，有，又因为 Pr≥c1，所以，且当时，有。故由Bernstein不等式：

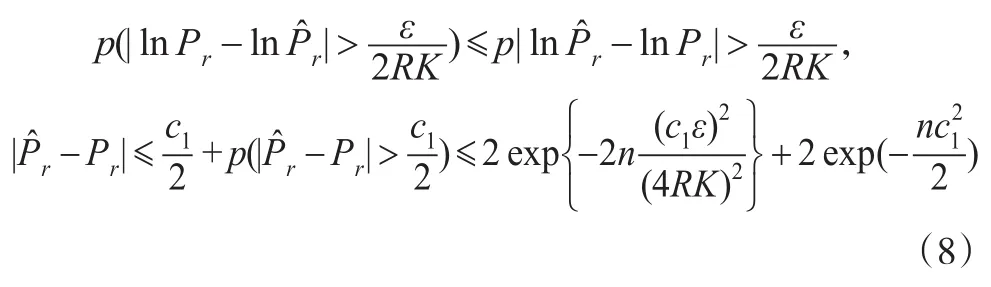
类似Liu等[5]引理4的证明，可得存在正数c3和c4，有：

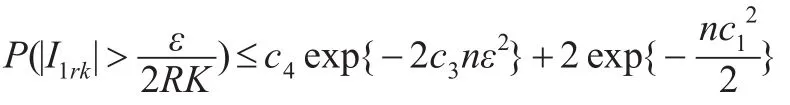
因此存在正常数满足：

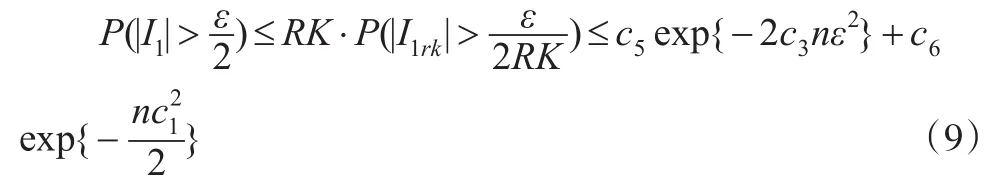
同理可得：

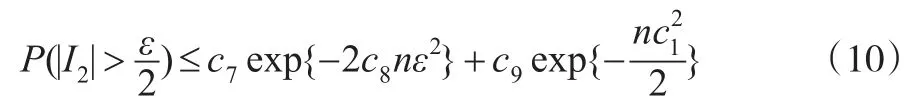
其中c3-c9都为正数。最终，由式（5）、式（9）、式（10）得到：

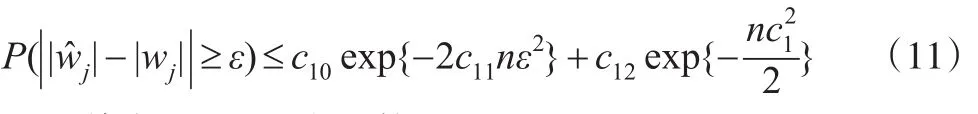
其中c10-c12为正数。

下面证明公式（3）。由条件（C2）可得对于某些j∈D，，若 D∉，则必存在某些 j∈D 使得＜cn-τ，即。所以：

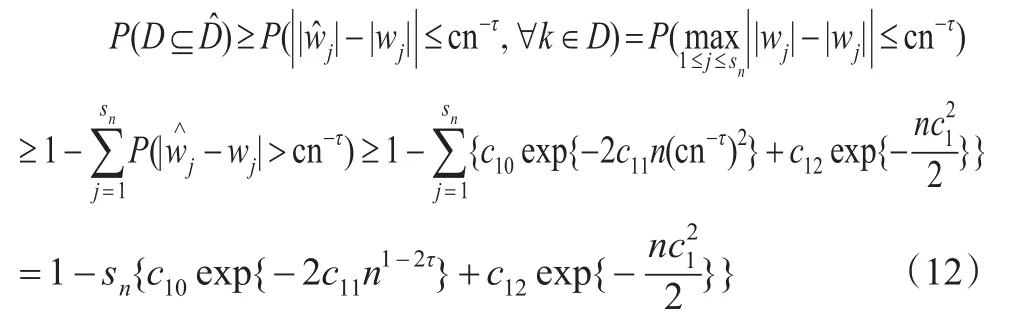
其中sn为D的基数。所以P(D⊆)→1。

5 结论

针对传统统计分析方法在超高维数据特征筛选方面的不足之处，本文在卡方检验特征筛选方法（PC-SIS）的基础上，提出了基于似然比检验的特征筛选方法（LR-SIS），LR-SIS具有无模型假设、计算简便、稳健性高的特点，允许响应变量与协变量之间存在任意回归关系，避免了筛选初期寻找准确回归模型的困难。在样本量较大时，LR-SIS的准确程度与PC-SIS方法相当，而在小样本情况下效果要优于PC-SIS。从数值模拟以及实例数据的分析结果表明，此方法对于高维数据特征筛选工作是合理有效的。