非参数下贝叶斯判别与聚类分析的信用指标筛选模型

刘雨萌，李战江，尹 伟,2

（1.内蒙古农业大学 经济管理学院；2.内蒙古银监局，呼和浩特 010010）

0 引言

微型企业由于自身财务制度不规范、财务信息不健全或者无力提供抵押担保等原因，面临着融资难的问题。构建一套科学、完整的能够判别微型企业违约状态的指标体系，可以为银行对微型企业进行科学评估和信用评价提供参考依据。

目前关于企业信用评价指标体系的研究：国际经典的“5C”原则从品质(character)、资本(capital)、能力(capacity)、担保(collateral)、经营环境(condition of business)五个方面对企业信用状况进行评价[1]。标准普尔（S&P）主要根据经营指标和财务指标这两类指标对企业进行信用评级[2]。美国穆迪（Moody）对企业的资本结构、销售增长等方面进行评价[3]。中国工商银行从股东情况、经济条件、发展前景、偿债能力等方面对企业进行信用评价[4]。中国建设银行的小企业信用评价指标体系，主要由财务风险、账户行为、经营环境、经营状况、发展潜力、实际控制人实力与资信等指标构成[4]。5C原则、标准普尔和穆迪的评价指标体系的共同特点是适用于评价大中型企业，不适用于微型企业。

而关于企业信用评价指标筛选方法研究，李战江（2017）通过Brown-Mood中位数检验、Moses方差检验以及Kendall秩相关检验筛选出了包含22个指标的微型企业信用评价指标体系[6]。赵志冲等（2017）通过似然比检验筛选出对违约状态有显著影响的指标，通过计算同一准则层内任意两个指标的相关系数删除对违约状态区分程度小的指标[7]。侯雨欣和王冲（2016）采用德尔菲法与因子分析相结合的方法进行信用评价指标筛选[8]。迟国泰等（2016）通过偏相关性分析进行了第一次筛选，基于Probit回归进行了第二次筛选，得到了由速动比率、总资产增长率等23个指标构成的指标评价体系[9]。迟国泰和陈洪海（2016）依据信息敏感性指标筛选标准确定累计信息含量，通过累计信息含量的大小遴选指标[10]。夏立明和迟媛（2015）运用信息沉淀法得到初步指标，应用因子分析降维，提取公因子，最终形成了由偿债能力、创新能力等六个因子组成的中小企业信用评价指标体系[11]。Li等（2013）利用投影追踪方法对信用评价指标进行筛选[12]。Hammer等（2012）通过逻辑回归方程的方法对评价指标进行筛选[13]。Sohn和Jeon（2010）运用Weibull模型进行指标筛选建立信用评价模型[14]。顾雪松等（2010）运用因子分析和聚类分析相结合的方法进行信用评价指标筛选[15]。

综观现有研究：一是现有文献都集中讨论参数下的指标筛选问题，少有使用非参数方法构建信用评价指标的筛选研究。二是现有文献在信息重复指标筛选时，大多使用参数聚类方法筛选信息重复指标，少有使用非参数方法筛选信息重复指标的研究。而现实是大多数评价指标不服从正态分布且分布未知，因此使用非参数方法筛选指标更加有效。基于此，本文将非参数贝叶斯判别与非参数聚类分析相结合，对信用评价指标进行双重组合筛选，最终构建了非参数下贝叶斯判别与聚类分析的信用指标筛选模型并进行了应用分析。

1 评价指标体系构建方法

1.1 指标数据的标准化方法

指标数据标准化的目的：将指标数值转化为[0,1]之间的数，消除指标和量纲的不一致，为微型企业信用评价指标筛选奠定基础。指标可以分为正向指标、负向指标、区间型指标和定性指标四类。

1.1.1 正向指标的标准化

正向指标是指数值越大，微型企业信用状况越好的指标，例如“营业利润率”。设xij是第i个指标第j个企业标准化后的值；vij是第i个指标第j个企业的原始值；n是企业总数。根据正向指标的标准化公式，则有[16]：

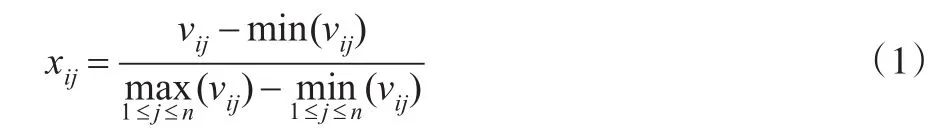
1.1.2 负向指标的标准化

负向指标是指数值越小，微型企业信用状况越好的指标，例如“未偿还贷款总额占资产总额比”。根据负向指标的标准化公式，则有[16]：

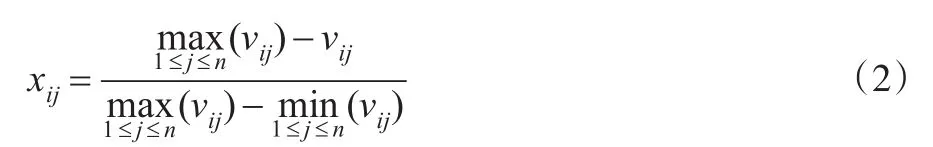
1.1.3 区间型指标的标准化

区间型指标是指数值越接近某一特定区间，微型企业信用越好，并且在这个特定区间内，信用状况最好的指标。本文中出现的两个区间型指标为居民消费价格指数和年龄，居民消费价格指数的理想区间为[101,105]，在该区间内表示既不通货膨胀也不通货紧缩。年龄的理想区间是[31,45]，企业法人处于这个年龄段表明他的还款能力和还款意愿最强。设q1是最佳区间左边界；q2最佳区间右边界。最佳区间指标的打分公式为[16]：

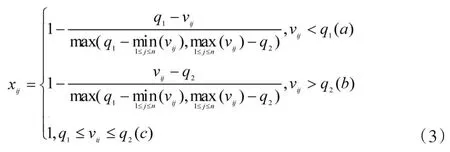
1.1.4 定性指标的标准化

对所有定性指标制定出适合微型企业的打分标准，将指标转化为[0,1]区间的数。所有23个定性指标的打分标准如表1所示。

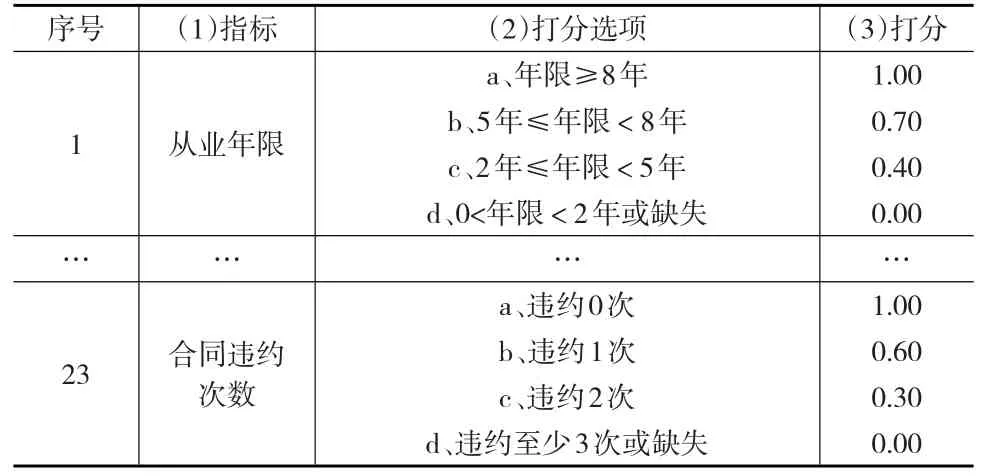
表1 定性指标打分标准

1.2 指标数据的正态性检验

由于指标的分布情况未知，首先应该对指标数据进行正态性检验，确定指标是否服从正态分布。本文选用K-S检验对指标数据进行正态性检验。

设Di第i个评价指标的K-S正态检验统计量值；Fi(x)是第i个评价指标的经验分布函数；μi是第i个评价指标的平均值；σi是第i个评价指标的标准差；m是评价指标的数目。则有[17]：

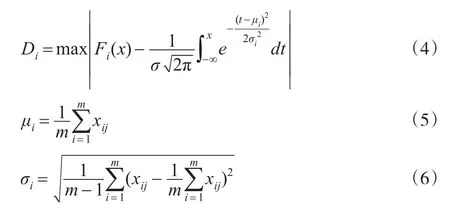
检验标准：在0.01的显著性水平下，比较评价指标的概率P值与0.01的大小。若第i个评价指标的概率P值小于0.01，则第i个评价指标不服从正态分布；若第i个评价指标的概率P值大于等于0.01，则第i个评价指标服从正态分布。

1.3 基于非参数Bayes判别的第一轮筛选方法

对全部指标进行非参数核密度Bayes判别，可以得到一个判别精度，去掉特定指标后，对剩余指标再进行非参数核密度Bayes判别，可以得到另一个判别精度。根据所得到的两个判别精度之间的差值，决定该特定指标保留或删除。

1.3.1 Bayes判别函数的建立

设P是样本来自第i个总体的后验概率；G1是违约企业总体；G2是非违约企业总体；x是待判样本；p̂i是样本来自第i个总体的先验概率；fi(x)是第i个总体的核密度函数；Bayes判别函数如下[18]：

式（7）的含义：样本来自第i个总体的后验概率等于样本来自第i个总体的先验概率与第i个总体核密度函数的乘积与样本来自各总体的先验概率与各总体核密度函数乘积之和的比值。

1.3.2 先验概率的计算

设ni是第i个总体的样本数，则样本来自第i个总体的先验概率为[19]：

式（8）的含义：样本来自第i个总体的先验概率等于第i个总体的样本数与全部样本数的比值。

1.3.3 核密度函数的确定

设hn是窗宽；K(x)是总体的核函数；Xij是第i个总

体中的第

i

个样本，则第

i

个总体的核密度函数为

[20]

：

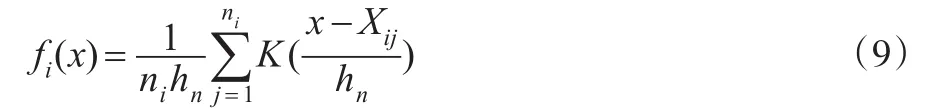
式（9）的含义：根据已知样本的数据和选定的核函数及窗宽，可以估计出总体的分布密度函数。

1.3.4 窗宽的选择

在选择最优窗宽hn时选用交叉验证法直接从现有的数据得到合理的窗宽，不需要对估计密度函数做任何假设。此方法选择窗宽hn使积分均方误差（IMSE）达到最小。则有[19]：

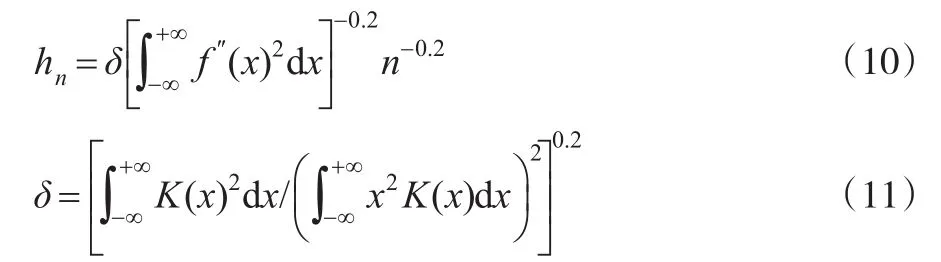
式（10）和式（11）的含义：窗宽的选择取决于密度函数的曲率，常数δ依赖于核函数。

1.3.5 核函数的选择

对于不用的核函数分别使用相应的最优窗宽，积分均方误差的差别不大，即最优窗宽的选择远比核函数的选择更重要，使用不同核函数得到的密度估计一般非常接近。本文中的核函数选用高斯核函数，则有[21]：

式（12）的含义：在高斯核函数中，离原点越近，核函数的取值越大，并在原点处取得最大值。

1.3.6 Bayes判别规则的确定

将由式（8）至式（12）计算得到的结果代入式（7），可以得到待判样本来自不同总体的后验概率，判断样本来自哪一总体的判别规则为[22]：

式（13）的经济学含义：若P(G1|x)＞P(G2|x)，说明样本来自G1总体的概率大于来自G2总体的概率，则待判样本属于违约样本；若P(G1|x)＜P(G2|x)，说明样本来自G1总体的概率小于来自G2总体的概率，则待判样本属于非违约样本。

1.3.7 判别精度的测算

设Ma是违约样本的判别精度；D是Bayes判别的违约样本数；n1是实际违约样本数，则有[23]：

式（14）的含义：D是由式（13）得到的违约样本数，违约样本的判别精度越大，说明判别的违约样本数与实际违约样本数越接近，指标体系的判别效果越好。

设Mb是非违约样本的判别精度；U是Bayes判别的非违约样本数；n2是实际非违约样本数，则有[23]：

式（15）的含义：U是由式（13）得到的非违约样本数，非违约样本的判别精度越大，说明判别的非违约样本数与实际非违约样本数越接近，指标体系的判别效果越好。

设M是全部样本的判别精度，则有[23]：

式（16）的含义：全部样本的判别精度等于违约样本的判别精度和非违约样本的判别精度的算术平均数，全部样本的判别精度越大，说明指标体系的判别效果越好。

1.3.8 基于Bayes判别指标筛选的具体步骤

步骤1:将所有样本n个指标标准化后的数据代入式（7）至式（16），可以得到n个指标的判别精度M0。

步骤2:剔除n个指标中的第1个指标，将剩余的n-1个指标代入式（7）至式（16），可以得到n-1个指标的判别精度M1。

步骤3:以此剔除n个指标中的第2,3,…,n个指标，将剩余的n-1个指标代入式（7）至式（16），可以得到n-1个指标的判别精度Mi。

步骤4:设Ci是第i个指标对判别精度的影响程度，则有：

式（17）的含义：第i个指标对判别精度的影响程度为去掉第i个指标后的判别精度与全部指标判别精度的差值，反映了第i个指标对指标体系判别精度的重要程度。

步骤5:测算所有指标对应的Ci值，根据Ci值与0的关系，决定指标的保留或删除。若删除第i个指标后的判别精度大于全部指标的判别精度，即Ci大于0，说明删除该指标后，指标体系的判别精度提高了，应该删除该指标；若删除第i个指标后的判别精度等于全部指标的判别精度，即Ci等于0，说明删除该指标对指标体系的判别精度没有影响，应该删除该指标；若删除第i个指标后的判别精度小于全部指标的判别精度，Ci小于0，说明删除该指标后，指标体系的判别精度降低了，应该保留该指标。

步骤6:设Yi是第i个指标对判别精度影响程度所占比重；|Ci|是第i个指标对判别精度影响程度的绝对值；k是Ci小于0的指标数；Y(k)是前k个指标对判别精度影响程度的累计比重。则有：

式（18）和式（19）的含义：根据对判别精度影响程度累计比重Y(k)≥95%的标准筛选指标[24]。将Yi按从大到小的顺序依次累加，当Y(k)≥95%时停止累加，保留累加的Yi对应的指标。

1.4 基于非参数聚类的第二轮筛选

对经过第一次筛选后保留的指标在同一准则层内进行非参数聚类，在聚成一类的指标中，删除非参数聚类中类是由概率密度函数的众数定义的，聚类过程中采用球均匀核密度估计的方法。设xt是第t个指标；n是指标数；nt是在xt的邻域内的指标数；vt是xt的近邻的体积，其中，把以指标xt为中心的球称为xt的邻域，在xt邻域内的指标称为xt的相邻指标。则有[25]：

式（20）的含义：概率密度的估计值为以该点为中心的球内的所含指标数除以指标总数和球的体积的乘积。

非参数聚类的具体步骤：

步骤1:首先将每个指标当作一个单独的类。

步骤2:对每一个指标，找到估计密度较大的最近的相邻指标，将它们所属的两个类合并。

步骤3:对于剩余的指标，找到其估计密度等于某些相邻指标的估计密度但不小于任何相邻指标的估计密度，合并含有这样指标的类。

步骤4:将聚成一类的指标中对判别精度影响程度较小的指标删除，即删除上文中计算出的Y值较小的指标，保留判别精度影响程度所占比重最大的信用指标。

2 应用

2.1 指标数据的标准化

根据标普、穆迪等国外金融机构以及中国工商银行、中国建设银行等国内金融机构构建的企业信用评价指标体系，最终建立了包含企业内部财务因素、企业内部非财务因素等6个二级准则层，相关行业从业年限等68个指标的海选体系。海选指标体系见表2第（b）列和第（c）列。

使用860个企业信贷数据为模型应用样本，将第（d）列中标有“正向”的指标所对应的信贷数据代入式（1），标准化后的数值放入表2第1～860列的相应行；将第（d）列中标有“负向”的指标所对应的信贷数据代入式（2），标准化后的数值放入表2第1～860列的相应行；将第（d）列中标有“区间”的指标所对应的信贷数据代入式（3），标准化后的数值放入表2第1～860列的相应行；对第（d）列中标有“定性”的指标根据表1进行打分，结果放入表2第1～860列的相应行；同时将860个样本分为违约和非违约两部分，30个违约样本列入表2第1～30列，830个非违约样本列入表2第31～860列，指标数据标准化的最终结果见表2。

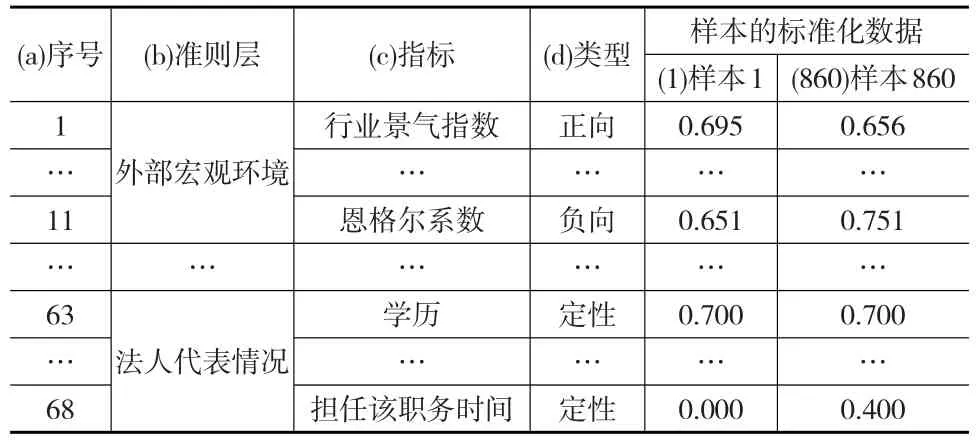
表2 标准化数据

2.2 指标数据的正态性检验

将表2中第1～860列的数据按行代入式（4）至式（6），得到所有指标的K-S检验的P值，由于计算量较大，应用SAS程序来完成对指标的正态性检验。结果显示68个指标的检验概率P值都小于0.01，可以证明所有指标都不服从正态分布。因此应该选择非参数方法对这68个评价指标进行筛选。

2.3 基于非参数Bayes判别的第一轮筛选

以三级准则层“法人代表基本情况”为例，说明非参数Bayes判别筛选指标的具体过程，三级准则层“偿债能力”包含的11个指标见表3第1列。

表3 非参数Bayes判别结果 （单位：%）

2.3.1 用11个指标进行非参数Bayes判别得到违约判别精度

将标准化后的数据依次代入式（4）至式（13），可以得到用11个指标进行非参数Bayes判别的结果，上述过程可以通过SAS程序来实现。再将判别结果依次代入式（14）至式（16），得到的违约样本判别精度Ma0、非违约样本判别精度Mb0以及全部样本判别精度M0。在30个违约样本中，有19个样本通过非参数Bayes判别被判定为违约样本，根据式（14），可以得到违约样本的判别精度Ma0并将结果列入表3第2列第1行。

在830个非违约样本中，有824个样本通过非参数Bayes判别被判定为非违约样本，根据式（15），可以得到非违约样本的判别精度Mb0并将结果列入表3第2列第2行。

将违约样本的判别精度Ma和非违约样本判别精度Mb代入式（16），可以得到全部样本的判别精度M0并将结果列入表3第2列第3行。

2.3.2 删除第i个指标后，用其余10个指标进行非参数Bayes判别得到违约判别精度

删除表3第1列第1行的指标“学历”，用其余的10个指标重复上文的步骤，可以得到删除“学历”指标后的其余10个指标的违约样本判别精度Ma=43.33%，非违约样本判别精度Mb=98.92%，全部样本判别精度M0=71.13%，分别列入表3第1行第3～5列。

同理，依次删除表3第1列中的第2,3,…,11个指标，用其余的10个指标重复上文的步骤，可以得到删除该指标后的违约样本判别精度Ma、非违约样本判别精度Mb、全部样本判别精度M0，分别列入表3第2～11行第3～5列。将表3第5列中删除特定指标后得到的全部样本判别精度Mi和第2列中全部指标的判别精度M0代入式（16），可以得到该指标对判别精度的影响程度Ci列入表3第6列的相应行。

2.3.3 根据指标对判别精度的影响程度进行指标筛选

根据表3第6列可知，“公司法人代表本地居住年限”和“性别”这两个指标的Ci值大于0，将这两个指标的Ci值列入下页表4第2列第1～2行，其余的9个指标按照Ci绝对值从大到小的顺序依次列入表4第2列第3～11行。

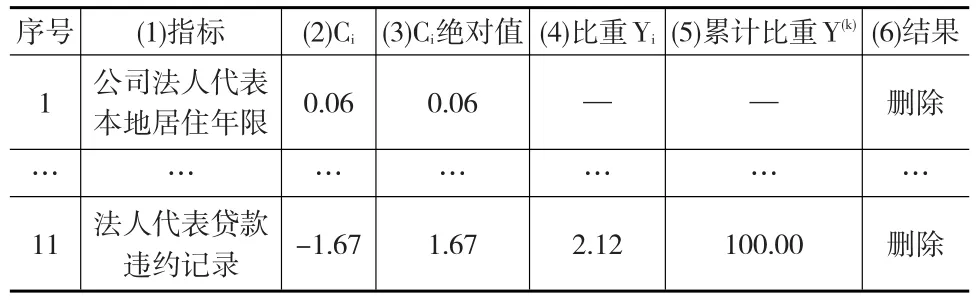
表4 非参数Bayes判别指标筛选结果 （单位：%）

根据上文中的筛选标准，表4第1列中前两个指标的Ci值大于0，说明删除指标可以提高指标体系的判别精度，因此应该将这两个指标删除。

将表4第3列第3～11行的数值代入式（18）可以得到每个指标对判别精度影响程度所占的比重，分别列入表4第4列第3～11行，将表4第4列第3～11行的数值代入式（18）可以得到前k个指判别精度影响程度的累计比重，列入表4第5列第3～11行，保留累计比重达到95%前所对应的指标，即保留表4中第3～10行所对应的指标，删除表4第11行所对应的指标。

根据以上筛选的过程，在三级准则层“法人代表基本情况”的11个指标中，有8个指标被保留，3个指标被删除，筛选结果列入表4第6列。

同理，对每一准则层重复上述筛选过程，可以得到全部指标的筛选结果，68个指标通过非参数Bayes判别的第一轮筛选，共有34个指标被删除，34个指标被保留。

2.4 基于非参数聚类的第二轮筛选

对第一次筛选后保留的34个指标在各自的准则层内进行非参数聚类。将标准化后的数据代入式（20）可以得到每个指标的估计密度，首先把每个指标当作一个单独的类；对每一个指标，找到估计密度较大的最近的相邻指标，将它们所属的两个类合并；对于剩余的指标，找到其估计密度等于某些相邻指标的估计密度但不小于任何相邻指标的估计密度，合并含有这样指标的类。由于此计算过程比较复杂，可以通过SAS程序来实现，非参数聚类的结果见表5。

表5 非参数聚类指标筛选结果 （单位：%）

表5显示：34个指标通过非参数聚类的第二轮筛选，共有14个指标被删除，20个指标被保留。

经过非参数Bayes判别的第一轮筛选和非参数聚类的第二轮筛选，68个指标中共有48个指标被删除，20个指标被保留，最终建立的信用评价指标体系见表6第2列。

2.5 指标体系合理性分析

2.5.1 指标体系与5C的对应分析

从表6可知，指标体系涵盖了5C原则包括的五个方面：品质、资本、能力、担保、经营环境。超速动比率等5个指标反映了5C原则的资本原则。年龄等11个指标反映了5C原则的能力原则。企业法律纠纷情况指标反映了5C原则的品质原则。GDP增长率等2个指标反映了5C原则的环境原则。抵质押得分指标反映了5C原则的担保原则。

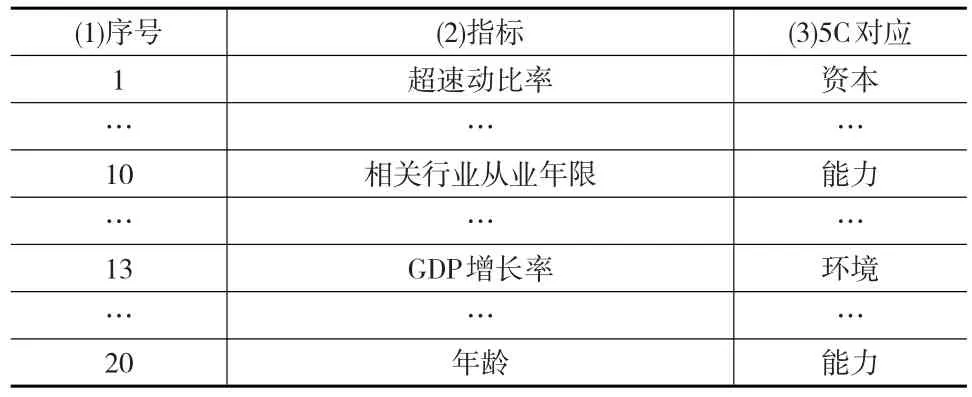
表6 最终构建的信用评价体系

2.5.2 海选指标体系与筛选后指标体系判别精度的对比

通过表7可以看出，经过两轮筛选后指标体系对于违约样本的判别精度由46.67%提高到了53.33%，对全部样本的判别精度由73.04%提高到了76.37%，说明由表6中20个信用指标构成的信用评价指标体系对于判别样本的违约状态具有更好的效果。

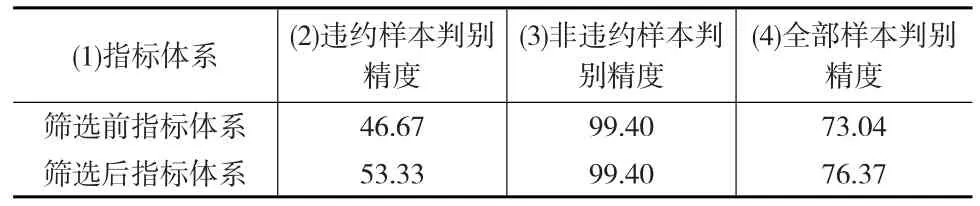
表7 筛选前后指标体系判别精度对比 （单位：%）

3 结束语

（1）通过非参数贝叶斯判别的第一轮信用指标筛选和非参数聚类的第二轮信用指标筛选，本文最终构建了非参数下贝叶斯判别与聚类分析的信用指标筛选模型并进行了应用分析。最终构建的20个信用指标涵盖了国际经典的5C原则所包含的五个方面。

（2）实证结果表明，海选指标体系的判别精度为73.04%，本文最终构建的指标体系的判别精度为76.37%，筛选后相比筛选前提高了3个百分点。

（3）通过非参数核密度方法估计出指标的分布函数并构建违约客户与非违约客户的二分类贝叶斯判别模型，删除判别精度影响度大于等于0的信用指标，保留判别精度影响度小于0的信用指标，确保保留的指标具有显著判别企业违约状态的能力。

（4）通过非参数聚类将第一轮筛选所保留的指标聚为19类，在聚为一类的指标中保留判别精度影响度比重最大的信用指标，避免了在删除冗余指标时，误删对判别违约状态影响大的指标。