混合序列完全矩收敛
费丹丹,付宗魁,王改霞,张 聪
(信阳学院 数学与信息学院,河南 信阳 464000)

对k≥0 令,有限子集S,T⊂N,且 dist(S,T)≥k},若存在kϵN,使得则称{Xn,n≥1}为混合序列。
混合序列是一类应用广泛的相依混合序列,许多学者对其进行了研究。文献[1-2]讨论了混合序列的完全收敛性和强收敛性;文献[3-4]研究了混合随机变量序列的几乎处处收敛性;文献[5]得到了混合序列的弱收敛性;文献[6]得到了不同分布混合随机变量序列的强收敛性。
1988年,Chow首先研究了独立同分布随机变量序列的完全矩收敛,得到了如下的结论:
定理1[6]设为独立同分布的随机变量序列,EX=0对任意的常数1≤p<2和r≥1使得,则有

随后,文献[7-8]讨论了ρ-混合序列的完全矩收敛。但是,对于混合列的完全矩收敛的研究很少。本文利用混合序列的矩不等式,得到了混合列的完全矩收敛。
引理1[9]设{Xn,n≥}1是随机变量序列,若存在一非负常数C,对 ∀x≥0及n≥1使得成立,对∀a>0,b>0,则有。
引理2[9]设是混合序列,,则存在一个仅依赖于的常数C,则有

引理3[10]设{Yi,i≥1}与{Zi,i≥1}是随机变量序列,对任意的t>1,ε>0,a>0,则有

在本文中,“<<”表示“O”,C在不同的位置表示不同的常数。
1 主要结果
定理2设{Xn,n≥1}是混合序列,存在一非负常数C,对∀x≥0及n≥1,使得成立,若

则有

定理3设{Xn,n≥1}是混合序列,存在一非负常数C对∀x≥0及n≥1使得成立,若,,对∀a>0,则有

2 定理的证明

定理2的证明由引理3知

对I由Markov不等式及引理2,由q≥2知



当,取q=2,由引理1得
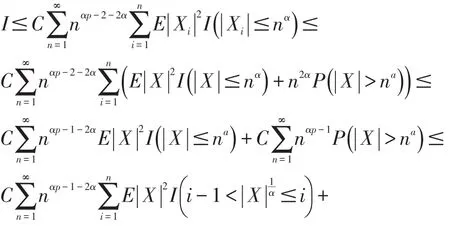

对II,由引理1得

因此,由(4)~(7)知定理 2得证。
定理3的证明在引理2中取s=2,则有

对III,由引理2知


对IIII类似(8)的证明,则有

因此,由(8)和(9)知定理 3得证。
3 小结
本文首先给出了混合序列的定义,随后介绍了独立同分布随机变量序列的完全矩收敛,并且讨论了混合序列的矩不等式。在此基础上,详细论述了混合序列的完全矩收敛。结果表明改变矩条件可以得到与独立同分布随机变量序列完全矩收敛类似的结论。

