基于Logistic回归的大学生助学金合理评定问题研究
杨朝越,唐 剑,丁 潇,汪云辰
(阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
近年来,我国高等教育阶段形成了以国家助学金、助学贷款、学费补偿、贷款代偿、勤工助学、困难补助、伙食补贴、学费减免等多种方式相结合的资助政策体系[1]。但每到高校助学金评定的时期,在学生中总会有不公平、不透明的议论,网上更是出现了高校助学金认定的“比穷演讲”,某生因用助学金购买名牌球鞋而被取消资助资格等案例。因此高校助学金评定问题还存在进一步完善的空间。随着大数据时代的来临,利用大数据挖掘技术与数学建模理论知识相结合的资助评判方式有助于提高学生资助工作的合理性和公平性,对加强学生资助管理具有重要意义。
国内学者的研究成果大致分为以下两种。一种是依据学生家庭经济状况,通过建立来指标评分体系法进行研究,另一种是利用层次分析、模糊综合评价等数学模型的方法来确定大学生助学金评价体系[2]。夏阳等人将指标定为操行等第、学习成绩、家庭情况、消费水平四类,并运用模糊层次分析法来评定助学金[3]。王明露等人将指标定为收入、助岗、交际花费、年级、民族五类,并运用泊松回归来研究[4]。唐业喜采用家庭、个人、学校、社会和特殊情况的“五维”高校贫困生精准认定指标体系,并运用层次分析法(AHP)和比较法(CM)相结合的模型进行研究[5]。张彦坤将指标定为生源地指标、家庭基础指标、学生在校支出指标、学生综合素质指标并以此来确定评分体系[6]。
国外对高校贫困生认定的方法较为客观,因其拥有较为完善的收入和税收统计系统,故大都基于客观数据来认定。如美国通过学生的教育成本和家庭能够分担的成本来确定学生的家庭经济状况;英国通过上年剩余收入及上年总收入减去购房分期付款及其他费用再核对家庭为学生负担的其他费用进行综合判定[7];德国通过学生父母上缴的个人所得税采用支付税单法;日本通过居民的资产指标、收入与各种分类采用权重指标相结合法等[5]。
参考国内外的研究成果,在高校助学金的评定中国内学者采用的层次分析法、模糊综合评价法较为主观,不能克服助学金评定问题中存在的人情因素和主观臆断,而国外的一些客观评定方法由于国情不同在中国难以广泛实施。综合考虑国内外的研究现状,通过客观的数据采集和客观数学模型的建立能够更好的解决助学金评定问题,基于此,本文将采用Logistic回归模型[8-9]对大学生助学金的合理评定问题进行深入研究。
1 助学金评定因素确定及分析
家庭经济困难的学生即学生家庭总收入无法承担起其在学校的生活和消费支出的学生。家庭经济状况能较为直接的反映其生活水平。影响其家庭经济状况的因素随着生活质量的不同而存在较大差异。如农村人口多以农业为主,故收入高低受气候、自然灾害等影响;如家中有慢性病(残疾)患者需长期治疗,则家庭经济状况受医疗支出影响。影响可以分为两类:直接影响与间接影响。学生家庭经济状况的直接影响实际上就是家庭收入与家庭支出,学生家庭经济状况的间接影响并非是通过收入与支出去直接影响,而是由于意外或突发状况等因素间接影响收入与支出,从而对家庭经济水平造成损失。通过参考已有的国内外研究成果中关于影响因素的确定和《高等学校学生及家庭情况调查表》以及《教育部财政部关于认真做好高等学校家庭经济困难学生认定工作的指导意见》等相关政策,最终将直接影响因素确定为学生月消费,家庭年收入;间接影响因素确定为生源类别,家庭健康状况,意外或突发状况,失业情况,孤儿、单亲、烈士子女,如图1。

图1 大学生助学金影响因素
本研究的因变量为二分类变量:需要资助和不需要资助,对于家庭贫困的学生应当予以适当的资助,反之则不需要资助。通过问卷调查的形式调查阜阳师范学院在校学生的家庭经济状况。从发放的1 300份问卷中,回收得到有效问卷1 139份。为克服偶然性和极端问卷对调查的影响,通过筛选抽样最终得出1 000份有效调查问卷,组织相关专家、学生辅导员以及学生构成民主评定小组,判定样本学生属于贫困还是非贫困。
由于学生月消费和家庭年收入数据过于复杂,将其进行分类量化,其余变量均用0-1变量表示,符合为1,不符合为0,如表1。
2 模型的构建与检验
2.1 Logistic模型概述
传统的线性模型默认因变量为连续变量,当因变量为分类变量时,传统线性回归模型的拟合方法方法会出现问题,因此人们继续发展出了专门针对分类变量的回归模型。此类模型采用的基本方法是变量变换,使其符合传统回归模型的要求。根据变换的方法不同也就衍生出不同的回归模型,相比之下,Logistic是使用最为广泛的针对对分类变量的回归模型。设因变量Y是一个二分类变量,其取值为Y=0和Y=1。影响取值的自变量分别为Xi。在自变量作用下结果发生的条件概率为P=P(Y=1|Xi),i=1,2,...,7则Logistic回归模型[8]可表示为:

表1 大学生助学金影响因素量化
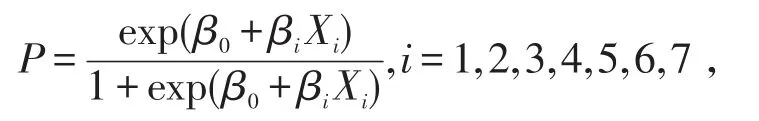
其中β0为常数项,βi为偏回归系数。经过Logit变换,Logistic回归模型可表示成如下线性形式:

当Z趋于+∞时,P值渐进于1;当Z趋于-∞时,P值渐进于0;并且随Z值的变化以点(0,0.5)为中心成对称形变化。
2.2 模型求解
2.2.1 合理性分析
模型的综合系数检验。由检验结果可知,P=0.0<0.05,说明模型变量中,至少有一个变量的值有统计学意义,即模型总体有意义。
拟合优度检验,P=0.981>>0.05,即样本数据中的信息已经被充分提取,模型拟合优度较高。
模型的综合系数检验和拟合优度检验结果说明模型的构建是合理的。
2.2.2 模型求解
Logistic回归模型的残差项服从二项分布而不是正态分布,因此不能使用最小二乘法进行参数估计,而是采用最大似然估计。
首先,建立模型,假设获取的样本为(xj1,xj2,…,xj7;Yj),其中j=1,…,1 000 ,则

Yj的概率密度可表示为:

其中,Yj=0,1。
Yj的极大似然函数为:
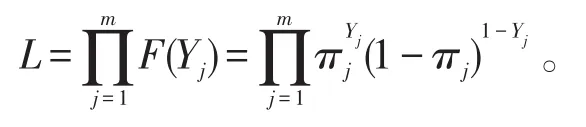
对数似然函数为:

设
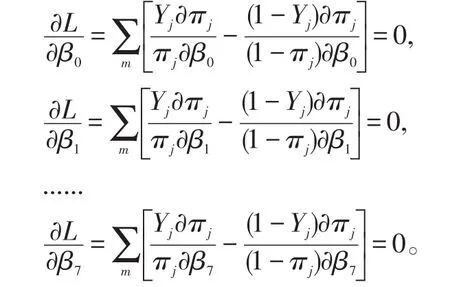
对下列各式进行检验

其次,求似然估计值,即对数似然函数最大时参数β0,β1,β2,…β7的估计值,利用 SPSS 软件[9]对1 000组数据进行分析得到估计结果,如表2。
最后,整理得出Logistic回归方程为

其中X1为学生月消费,X2为家庭年收入,X3为生源类别,X4为家庭健康状况,X5为意外或突发状况,X6为失业情况,X7为孤儿、单亲、烈士子女。
由模型可知当P∈[0.5,1],则需要资助,反之则不需要。该判别过程的流程图如图2所示。
2.3 模型检验
图3是预测概率的直方图,横轴为获取助学金的预测概率(0为不能获取,1为能获取),纵轴为观测的频数,符号“1”代表能够获取,“0”代表不能获取。若预测正确,所有的1均应在横轴(0.5,1)这个区间内,所有的0均应该在(0,0.5)这个区间内,由于样本数据较大,图中每个“0”、“1”均代表20个案例,所以总体上呈“U”型,两边数据多,中间数据少,能够较为直观的反映本模型对于助学金评定工作的预测较好。
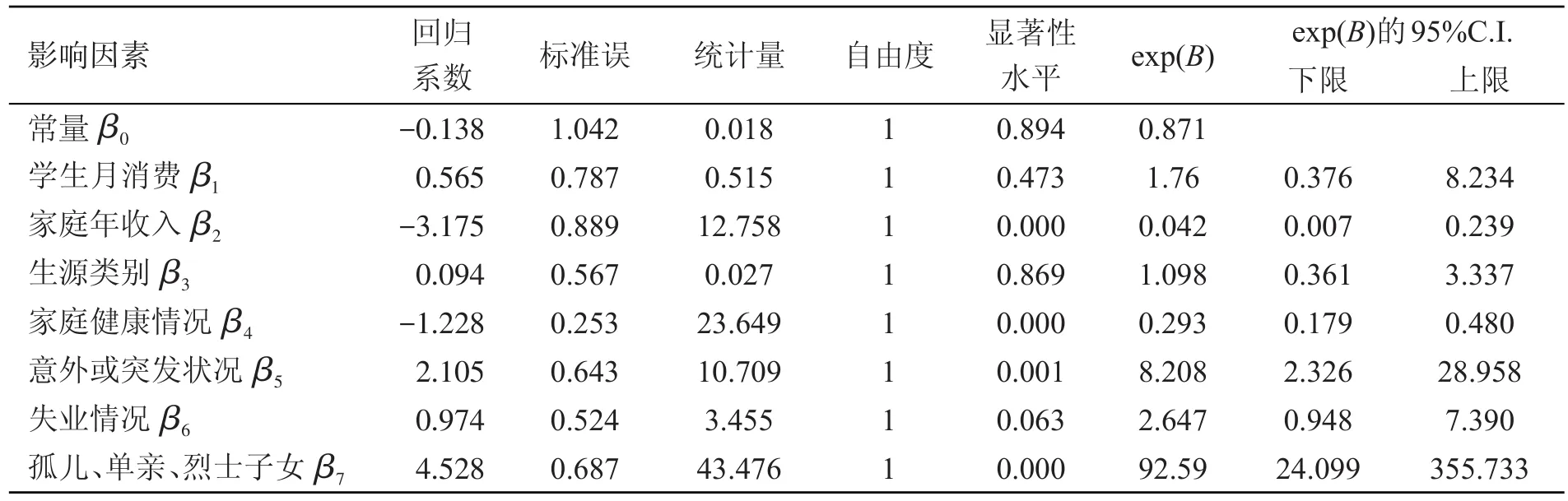
表2 模型系数的最大似然估计结果
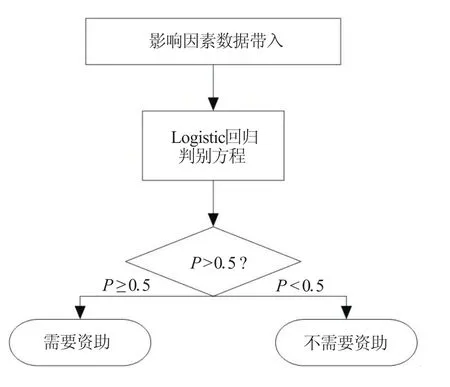
图2 判别流程图
为了进一步检验模型的真实性,随机选取100组样本带入检验。检验结果显示,Logistic回归模型预测的值与真实值基本一致。
综上所述,通过预测概率直方图代入样本数据检验,都可以说明Logistic回归模型能过很好的解决助学金评定问题。
3 小结
此项研究利用数学建模理论,采用大数据分析技术,通过建立Logistic回归模型,只要将确定的直接影响指标学生月消费,家庭年收入和间接影响指标生源类别,家庭健康状况,意外或突发状况,失业情况,孤儿、单亲、烈士子女的数据量化指标带入模型中通过对Logistic模型所得出的结果进行综合评估,当模型所得到的概率值时即可获取助学金,反之则不可获取助学金,这样的助学金的评价体系,可以帮助学校和政府资助工作者科学有效的去评定及发放助学金给困难学生和发现“隐性贫困”与疑似“虚假认定”学生,将有助于提高学生资助工作的精准度和公平性,是加强学生资助管理的新模式。本研究是以阜阳师范学院为调查地,由于不同学校所属的地区可能生活水平经济状况不同,模型的参数可能不同,但无论对什么学校,构建模型的过程和判别方法都适用。本文的结论是基于阜阳师范学院收集到的数据而言的,所以建立的模型具有一定的局限性和针对性。但从解决方法和模型构建上说,当样本容量较大、涉及面较为广泛时,本文的研究仍具有一定的参考和指导价值,随着资助区域不断发展和扩大,我们还可以将此模型运用到一个城市或者一个地区的资助工作中去,进一步提高资助工作的普及范围。

图3 预测概率直方图

