基于BP神经网络的锂离子电池SOC估计研究
雷 雨,李 锐,余佳玲,高 磊
(1.陆军工程大学通信士官学校,重庆 400035;2.山东省烟台市计量所,山东 烟台 264000)
关键字:锂离子电池;荷电状态(SOC);BP神经网络
由于近年来民用锂离子蓄电池动力电源行业特别是纯电动汽车的兴起,对于锂动力电池管理系统的研究也越来越多,而锂动力电池组的实时状态评估,包括容量估计和寿命估计是其中的一个研究重点。
锂离子蓄电池是个复杂的电化学系统,它在不同负载和环境条件下运行时,锂离子蓄电池实际可供释放的电量也不同。目前,国内外普遍采用荷电状态SOC来表示蓄电池的剩余容量,锂离子电池剩余容量的常用估计方法如下:1)开路电压法[1]。通过测量蓄电池的开路电压,推算蓄电池的剩余电量。开路电压与容量有较好的对应关系,但由于开路电压是电池无载时的稳态电压,因此只能在电池静置时(此时,不得不中断电池正在进行的工作)方可测量,不适合实时在线测量;2)安时积分法[2]。是将电池的充放电电流与充放电时间进行积分,得出的结果便是电池充放电容量,将此结果与电池的原始容量相加(放电时相减),便可预估剩余容量。这种方法应用简单而且计算量小,但要求标定SOC初始值,且存在着误差累积,在高温状态和电流波动剧烈的情况下误差较大,所以单独使用此方法预估精度很难得到保证;3)具有人工智能的新型算法。
1 人工神经元与BP神经网络
为了对锂离子电池状态估计与寿命预测方法进行探索研究,本人在实验室利用电池程控测试仪,对额定容量为1500mAh的磷酸铁锂电池进行充放电循环实验(实验步骤:300mA恒流充电至3.65V——3.65V恒压充电至电流小于10mA——静置1h——300mA恒流放电至2.5V)。随着实验的开展,笔者通过每天观察,对电池的荷电状态获得了某些“感性认识”:当电池的电压高于3200mV时,电池的剩余容量还比较充足;当电池的电压低于3000mV时,电池的容量已经不够。
可以利用人工神经网络,来模拟人脑对电池剩余容量的“感性判断”。人工神经网络的基本单元是人工神经元。
1.1 人工神经元
人工神经元[3],是人工神经网络的基本单元,它是一个多输入、单输出的非线性组件,如图1所示。
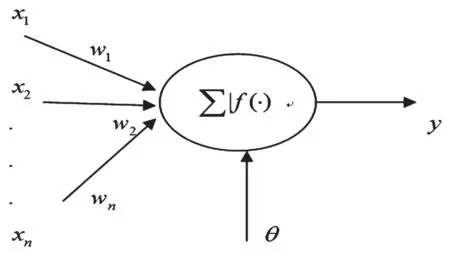
图1 人工神经元示意图
其输入与输出的关系为:
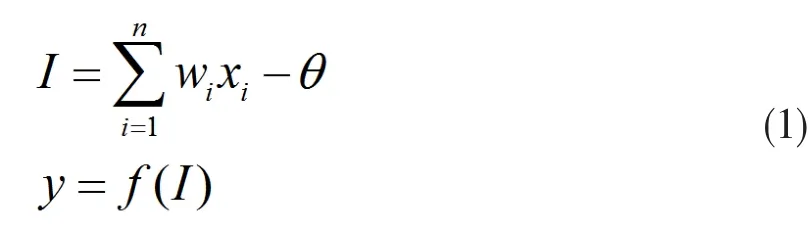
式(1)中, xi( i = 1,2,···,n )是从其它神经元传来的输入信号,或者是来自外部的信息;Wi表示从神经元i到本神经元的连接权值,也称加权系数,它表示神经元之间的连接强度,取值通常动态变化,由神经网络的学习过程确定;θ为神经元内部阈值;f(·)为激励函数,决定了神经元的输出。
1.2 BP神经网络
BP神经网络[4]是1985年提出,其网络典型结构如图2所示。
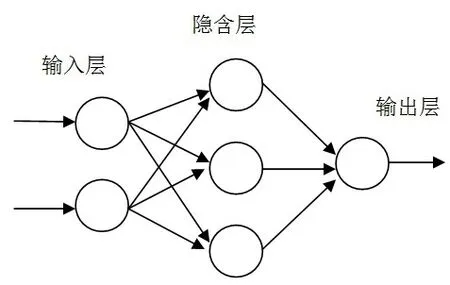
图2 BP神经网络典型结构
BP神经网络算法的学习规则[5]分为两个阶段,第一阶段为信号的正向传播过程。给定输入信息通过输入层经隐含层逐层计算,最后计算出每个单位的实际输出值;第二阶段为误差反向传播过程,若在输出层未能得到期望的输出值,则逐层递归地计算实际输出与期望输出之间的误差均方值,用于调节各层的加权系数,以期使输出的误差信号最小。
BP神经网络目前已成为应用最为广泛的一种人工神经网络模型,它的非线性数据结构和计算过程使得它适于处理非线性映射关系。
锂离子电池的端电压与SOC的关系就是一种非线性映射关系,以57#实验电池在第1次充放电循环的数据为例(300mA恒流放电),作图如图3所示。
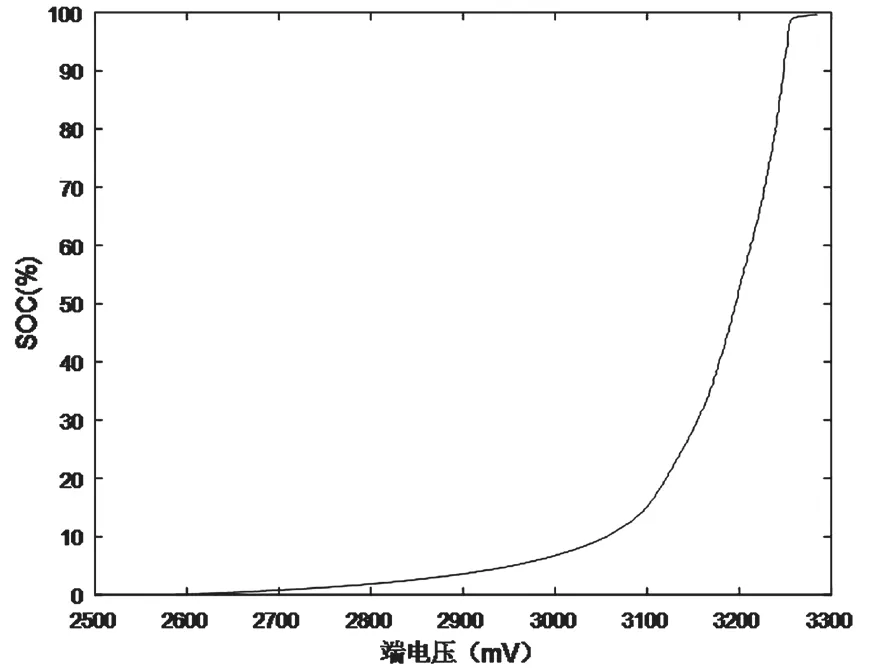
图3 锂离子电池端电压与SOC对应图
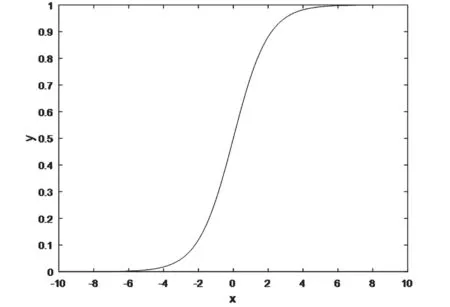
图4 Sigmoid函数曲线
由于Sigmoid函数 的图形与锂离子电池端电压、SOC对应图形相类似,因此,BP神经网络的激励函数可以采用Sigmoid函数。
1.3 最速下降法
在BP神经网络学习过程中,需要求目标函数(误差平方求和)的最小值。为了加快学习速度,增强时效性,采用最速下降法作为BP神经网络各层加权系数调整的算法。
由方向导数的概念,可得,负梯度方向为函数值下降最快的方向,最速下降法的基本步骤如下:
(1)选择初始点x(1),置k=1,设置最大迭代次数N;
当到达最大迭代次数时,算法终止。第(3)项为一维搜索,可以采取不同的搜索步长进行试探,取使目标函数值最小的步长的方式进行简化。
2 单神经元BP神经网络的SOC估计
学习样本为57#实验电池在第1-10次充放电循环时的数据,取特定SOC(90%、80%、70%、60%、50%、40%、30%、20%、10%) 时电池端电压的均值,并对放电电流、端电压数据进行标准化处理:
网络的结构图如图5所示。
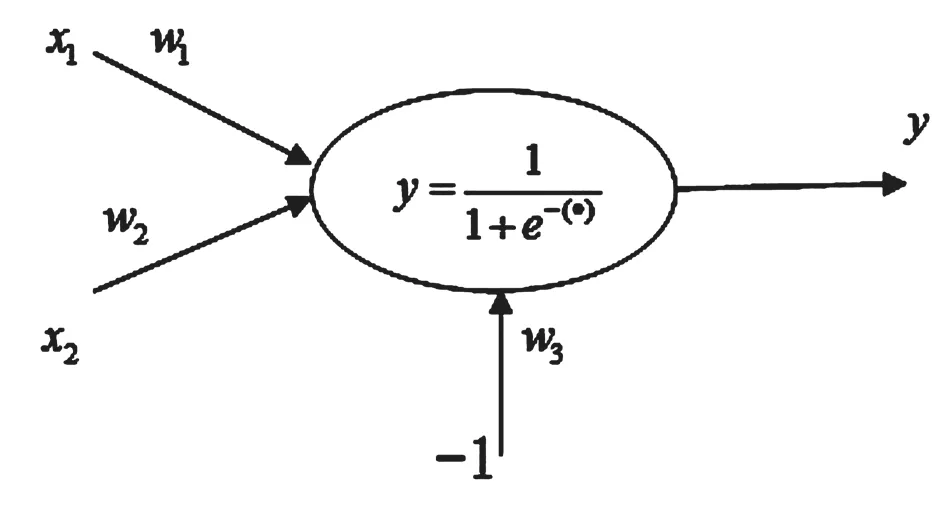
图5 单Sigmoid神经元网络
57#实验电池在第1-10次充放电循环恒流放电时,端电压均值与SOC值的对应关系如表1所示。
以表1数据为学习样本,使用Matlab进行仿真实验,单Sigmoid神经元网络学习结果如下:
其中,n代表学习样本数量,本例样本SOC值从10%到90%,共计9个学习样本,因此n=9;yi为第i个学习样本的输出值,为第i个样本的神经网络预测输出值,且有:
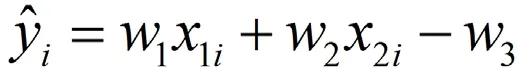
x1i、x2i为第i个学习样本的标准化输入值。
学习的均方误差为4.9582。
利用对第1-10次实验数据学习得到的模型,预测第11次充放电循环的SOC,结果如表2所示。
57#电池单神经元BP神经网络SOC估计误差图(取绝对值)如图7所示。
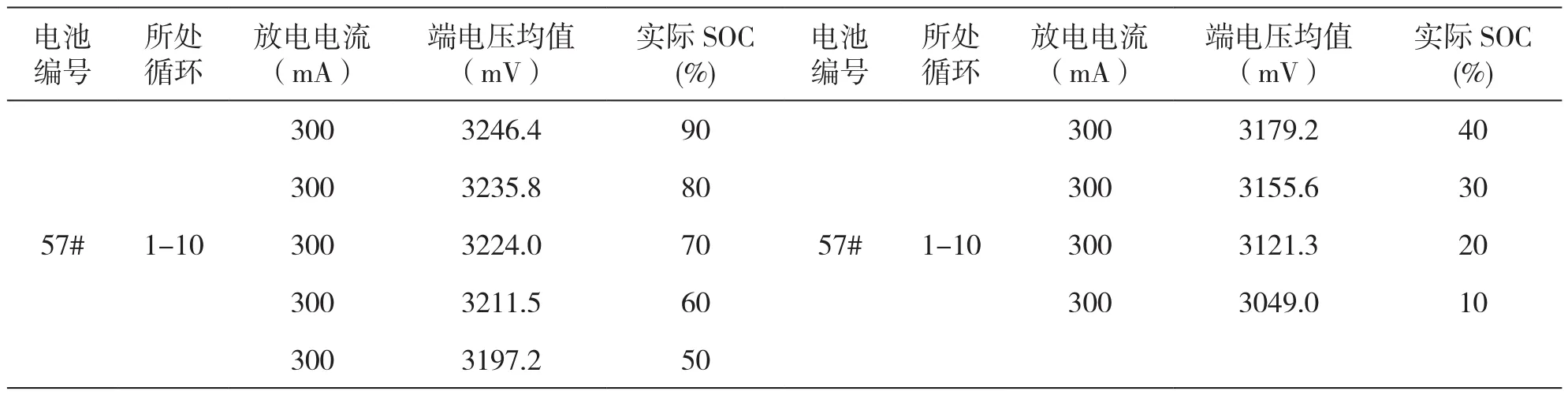
表1 57#实验电池1-10次循环恒流放电平均数据
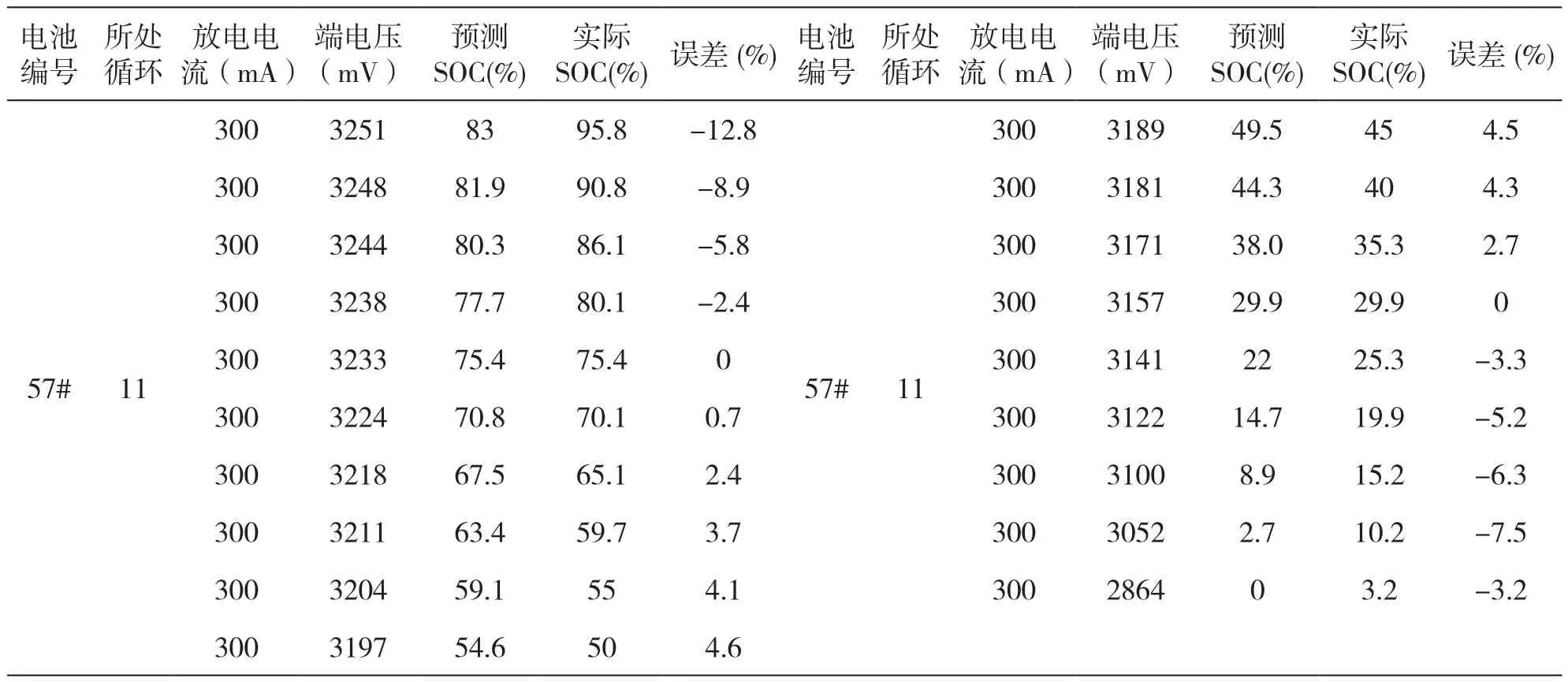
表2 单Sigmoid神经元网络预测结果
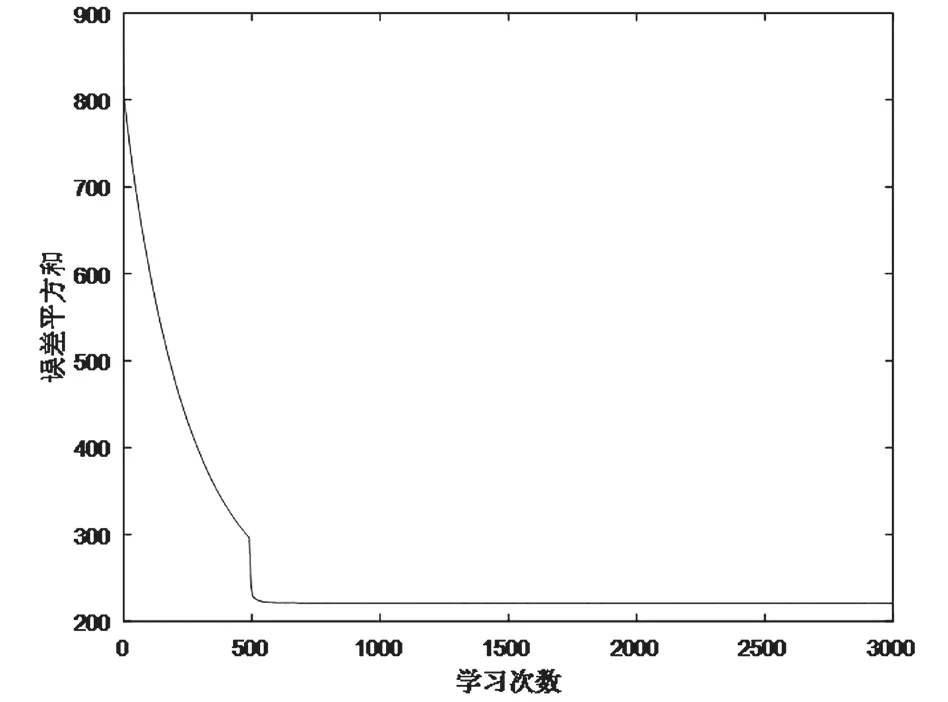
图6 57#实验电池单Sigmoid神经元网络学习误差(误差平方和)收敛曲线
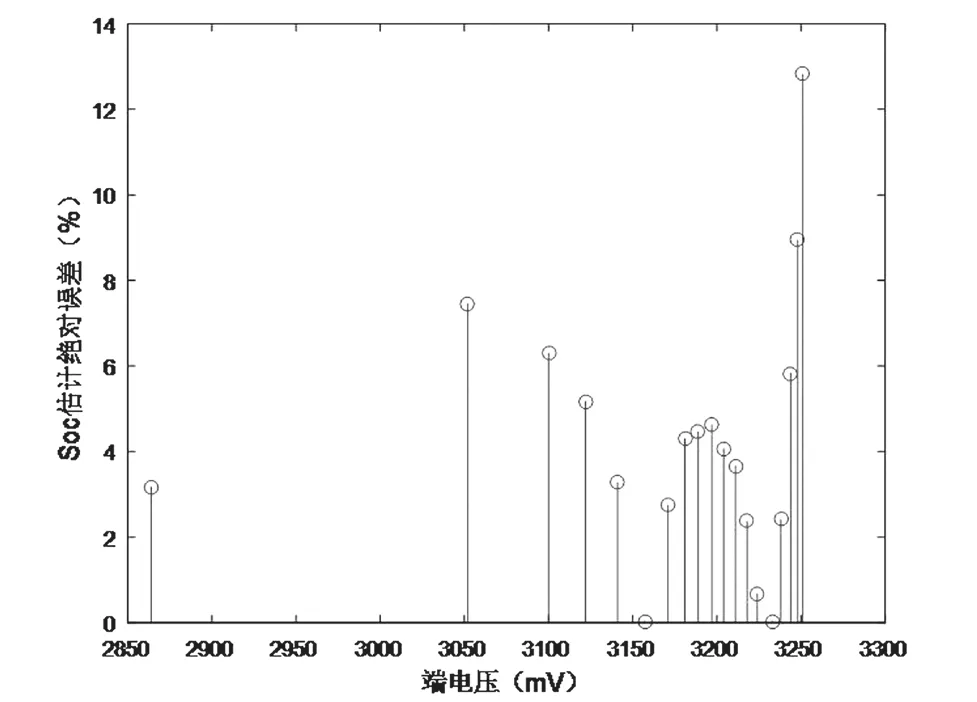
图7 单Sigmoid神经元网络SOC估计误差图
可以看出,放电初始阶段(SOC:90%—100%)时误差较大,其余阶段绝对误差一般小于8%。为了修正放电初始阶段的误差,可以增加一个激发函数为Sigmoid函数的神经元,作为误差修正神经元。
3 双Sigmoid神经元BP神经网络的SOC估计
学习样本仍然采用57#实验电池在第1-10次充放电循环时的数据均值(表1),对放电电流、电池的端电压的数据进行的标准化处理仍如单神经元网络。
双Sigmoid神经元网络结构图如图8所示。
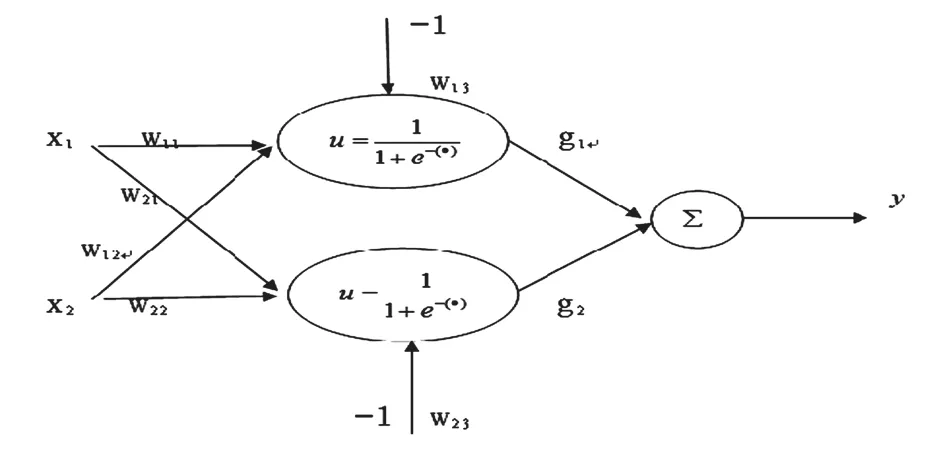
图8 双Sigmoid神经元网络结构图
使用Matlab进行仿真实验,样本(见表1)的学习情况如下,连接权值向量(与图8网络结构对应)有:
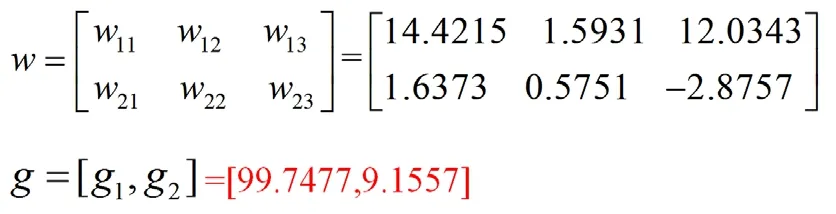
误差平方和ε = 56.0605,其在学习进程中的收敛曲线如图9。
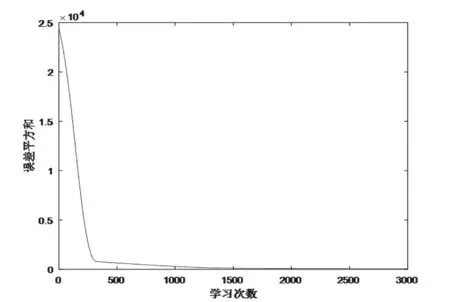
图9 57#实验电池双Sigmoid神经元网络学习误差(误差平方和)收敛曲线
网络学习均方误差ξ=2.4958,学习误差小于单神经元网络。
由g=[g1, g2]=[99.7477,9.1557]可见,第一个Sigmoid激励函数神经元为主体(g1>>g2),第二个Sigmoid激励函数神经元的主要作用为误差修正。
两种模型对第11次实验的电池SOC预测情况分别如表2、表3。
双Sigmoid神经元网络预测结果(表3)与单神经元BP神经网络的容量预测(表2)结果进行对比,图10为57#电池第11次充主电循环Soc预测误差对比。
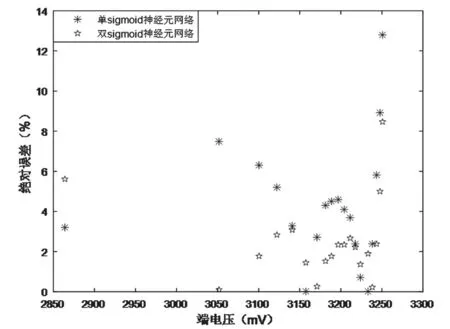
图10 单Sigmoid神经元与双Sigmoid神经元网络对SOC误差预测的对比图
根据图10,就第11次充放电循环采集的数据而言,采用双sigmoid 激励函数神经元时,SOC预测结果要明显优于采用单sigmoid 激励函数神经元。
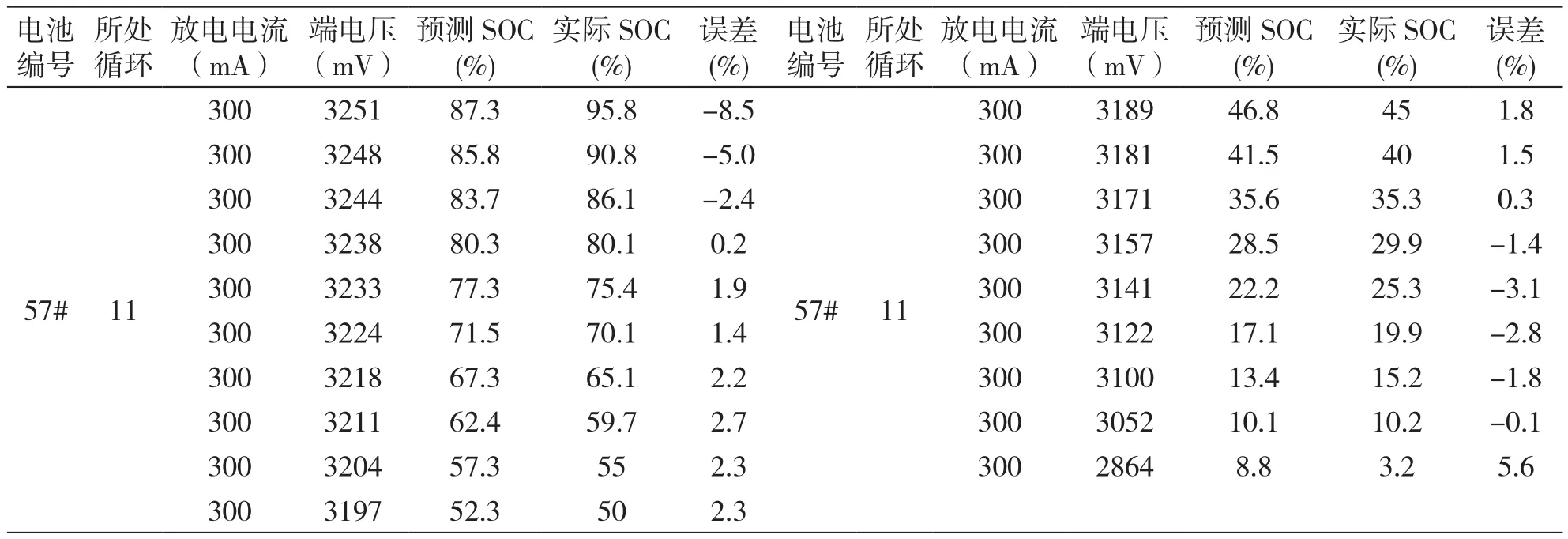
表3 双Sigmoid神经元网络预测结果
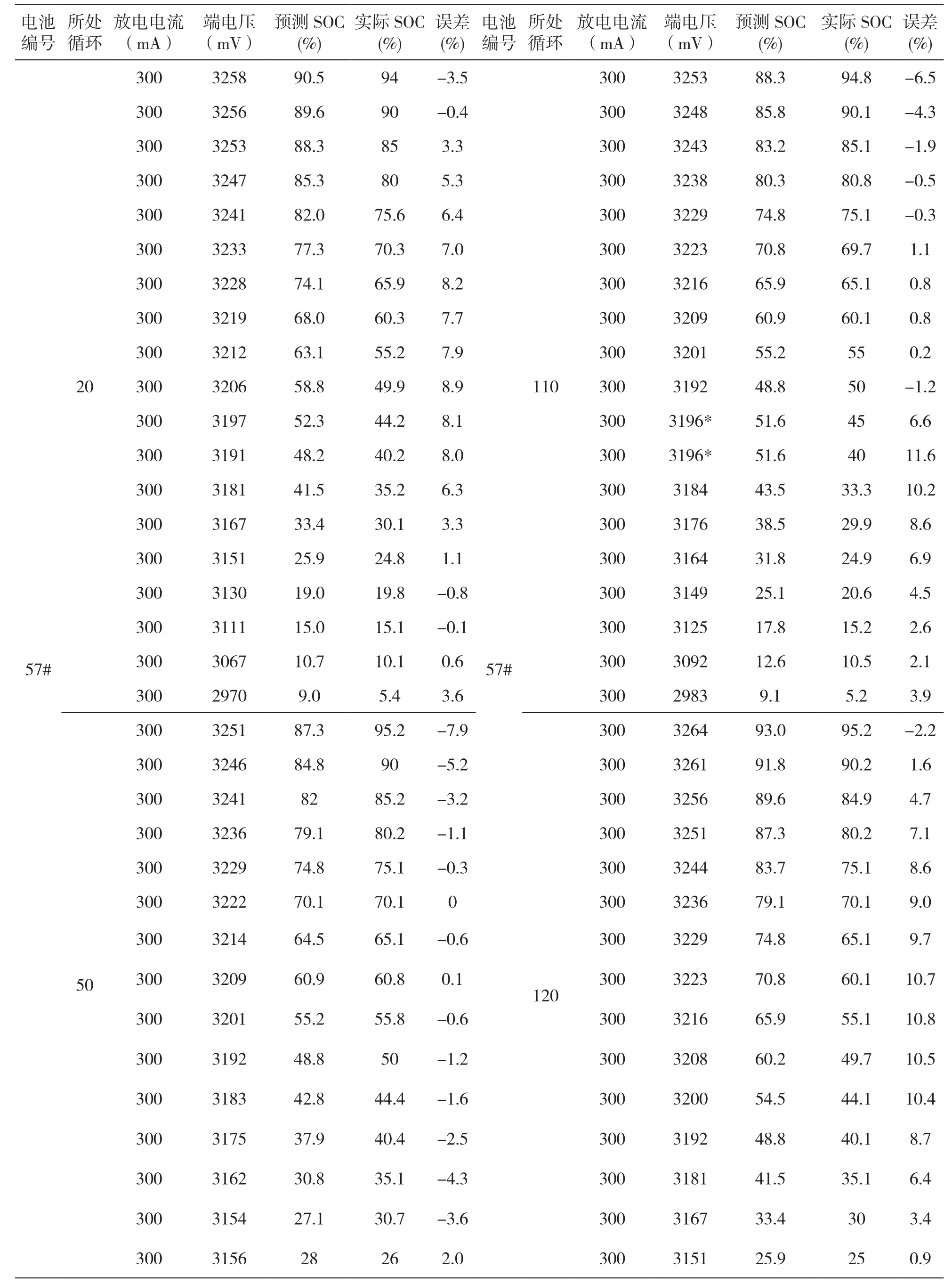
表4 双Sigmoid神经元网络模型预测结果
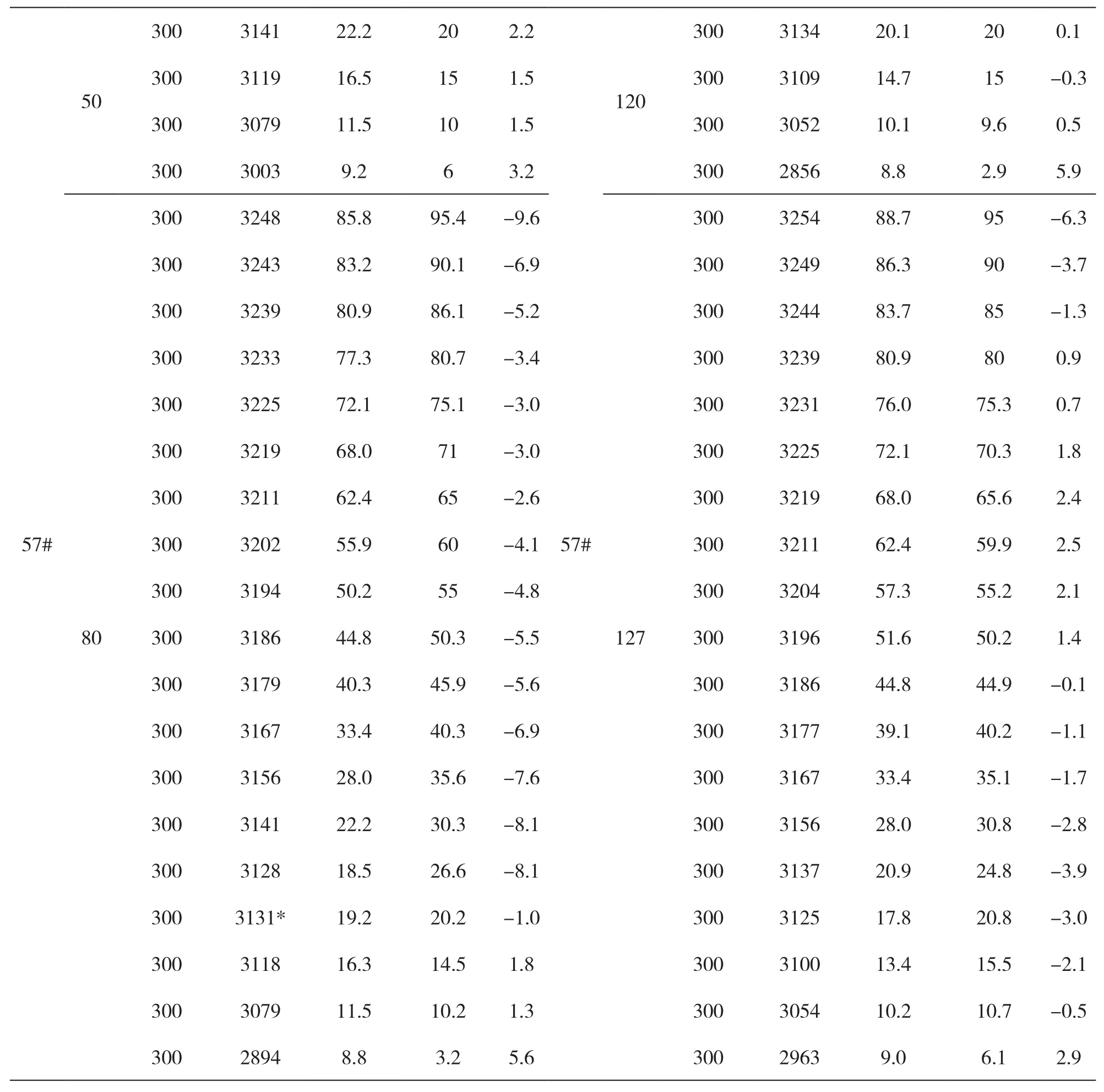
注:“*”处为异常端电压测量值,端电压随着放电过程的进行,不降反升,产生的原因可能是引入了测量噪声。
根据对第11次充放电循环中Soc进行预测的结果,采用双sigmoid 激励函数神经元时,放电开始阶段(SOC:90%-100%)的误差尽管比单神经元网络小,但仍较其它时间段大,在这一时间段里,端电压的变化较剧烈,类似指数形状下降;在放电终期(SOC: 0%-10%),误差也显著增大;在中间阶段(SOC:10%-90%),SOC预测较准确,绝对误差一般小于3%。
4 模型检验
需要检验随着充放电循环实验的进行,模型是否能持续进行准确的SOC估计。
采用第20、50、80、110、120、127次充放电循环时放电实验数据检验含有双sigmoid 激励函数神经元的BP神经网络模型,预测结果见表4表示。
从实验结果分析,当不考虑放电初始阶段(电极附近电解液与离电极较远处的电解液形成稳定浓度差以前,端电压迅速下降,下降部分与指数函数类似)、出现异常端电压测量值时及附近的时间段,双Sigmoid神经元网络模型在相当长的循环使用周期内(例如本实验中,第127次循环使用过程中的电池SOC,仍可通过模型做出较精确的预测)对SOC的预测误差一般不超过10%,符合动力电池电荷状态估计的精度要求。
5 结论
采用基于误差反向传播神经网络(BP神经网络),结合收敛速度较快的最速下降法而形成的锂离子电池荷电状态(SOC)估计算法,可以在较长的循环使用周期内,在经过一段相对稳定的工况后(即采用维持某电流放电3-5分钟后的数据,避免在浓差极化电压形成过程中端电压快速变化的不稳定阶段判断电池的SOC),通过放电电流与端电压较准确地估计电池的SOC,且网络结构简单,具备学习能力,易于工程实现。但本文的实验是在恒流(300mA)放电、电池寿命尚未到达终点(循环使用127次,容量尚未下降至额定容量的80%,在寿命的初、中期,电池内阻基本保持稳定)的情况下进行的,随着实验进一步深入(电池循环使用次数将逐渐接近循环使用寿命,电池内阻在寿命末期有较大变化;此外,还将进行不同倍率恒流、变负载条件下的电池放电实验),还有更多工作需要继续开展。

