模块神经元网络中耦合时滞诱导的簇同步转迁*

王蔓蔓 杨晓丽

（陕西师范大学数学与信息科学学院，西安 710062）

模块神经元网络中耦合时滞诱导的簇同步转迁*

王蔓蔓 杨晓丽†

（陕西师范大学数学与信息科学学院，西安 710062）

利用Courbage-Nekorkin-Vdovin神经元构建含有耦合时滞的模块神经元网络模型，通过数值模拟研究了耦合强度及耦合时滞对模块神经元网络簇同步放电特性的影响.研究结果表明，适当大的耦合强度可以诱导模块神经元网络达到簇同步.同时，研究发现耦合时滞可以诱导模块神经元网络出现簇同步转迁，且当时滞大小约为网络中所有神经元平均振荡周期的整数倍数时，模块神经元网络的簇同步现象能够间歇性出现.此外，研究结果表明时滞诱导的簇同步转迁对子网络内的耦合强度、子网络间的连接概率具有鲁棒性.

模块神经元网络， 耦合时滞， 簇同步转迁

引言

同步现象在自然界中普遍存在，它是物理、化学、生物等诸多领域的热门研究课题.在神经科学中，已有研究发现神经元的同步活动对大脑信息处理发挥着重要作用［1-2］.这引起众多学者关注大脑神经元网络的同步动力学，特别是在簇放电神经元的同步类型、不同的同步模式（如峰同步和簇同步）之间的关系、网络拓扑结构参数与同步的关系等方面取得很多研究成果［3-8］.

由于神经元间信息传递速度的有限性，耦合时滞在神经元网络中是不可避免的，越来越多的研究关注时滞对神经元网络动力学的重要作用.例如，在无标度神经元网络中，Wang等［9］通过数值模拟研究了耦合时滞对神经元网络同步的影响，发现随着时滞的增加，神经元网络的完全同步能够间歇性出现；Jalili［10］研究了时滞对小世界神经元网络峰同步的影响，通过数值模拟发现无论是兴奋性化学突触耦合还是抑制性化学突触耦合，合适的时滞都能增强网络的峰同步.最近关于猫和猕猴的脑皮层区域的研究表明，脑神经元网络在结构上具有模块特性［11-13］.因而，模块神经元网络（即网络的网络）的动力学行为逐渐引起科研工作者的关注.例如，针对模块上是小世界网络的模块神经元网络，Batista等［14］研究了簇放电神经元的同步行为；文献［15］探究了混合突触作用下时滞对模块神经元网络簇同步的影响，研究表明耦合时滞对耦合强度诱导的簇同步具有抑制作.Jia等［16］研究了具有参数异质性的模块神经元网络的多重共振行为；文献［17］研究了电耦合和化学耦合共同作用下时滞对模块神经元网络同步转迁的影响，发现时滞可以诱导模块神经元网络的完全同步发生转迁.

现有研究结果表明，时滞对神经元网络的同步特性、同步转迁具有关键性影响.但是在模块神经元网络中，耦合时滞对神经元网络动力学影响的研究结果还不是很多，许多科学问题还有待进一步研究.对于具有化学耦合的模块神经元网络，耦合时滞能否诱导模块神经元网络的簇同步发生转迁？模块神经元网络的拓扑结构参数对簇同步有什么影响？通过查阅文献，我们发现这些问题还没有得到研究.因此，本文将构建节点上是Courbage-Nekorkin-Vdovin（CNV）神经元的模块神经元网络模型，通过定义簇同步指标，利用数值模拟方法，研究耦合时滞对模块神经元网络簇同步动力学特性的影响.

1 网络模型和簇同步指标

1.1 网络模型

构造一个含有MN个神经元的模块网络，模块网络是由几个子网络组成的，且子网络可以是规则、无标度或小世界网络.由于模块网络的特点是：模块内部的节点连接比较紧密，模块间节点的连接则比较稀疏.因此模块网络的构造方法为：先生成M个子网络且每个子网络中含有N个节点，然后从第I个和第J（I，J＝1，2，…，M，且J≠I）个子网络中随机地选取一对节点，并且以概率pinter在选取的节点对之间引入一条边，按照上面这种方法可以构造出模块网络.在本文中所考虑的模块网络的每个子网络都是NW小世界网络.根据Newman和Watts［18］的思想，具有NW小世界特性的网络可以按照如下的方法构造：从一个节点总数为N的环状最近邻耦合网络开始，其中每个节点都与它左右相邻的各k/2个节点相连（k是偶数），然后以概率在随机选取的一对节点之间加上一条边，这样就生成了一个NW小世界网络.本文模型的参数设为：M＝2，N＝50，k＝6，第一个子网络内的加边概率为Pintra1＝0.05，第二个子网络内的加边概率为pintra2＝0.1.

利用一个二维离散的CNV神经元模型［19-20］描述模块神经元网络中单个神经元的局部动力学，且神经元间的耦合方式为兴奋性化学耦合.从而模块神经元网络的动力学方程为：

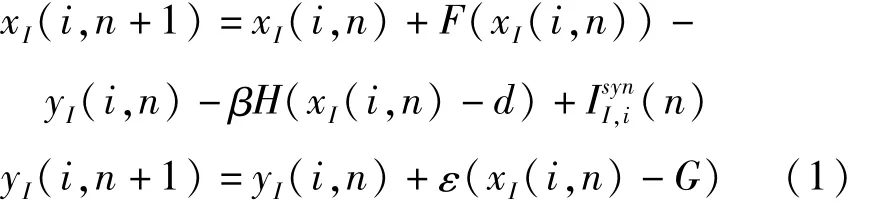
其中，xI（i，n）和yI（i，n）分别表示第I（I＝1，2，…，M）个子网络中第i（i＝1，2，…，N）个神经元在n时刻的膜电位和恢复变量，ε（ε＞0）代表恢复变量的速率，参数β，d，G控制生成信号的形状，.当参数值为a＝ 0.1，β＝0.3，d＝0.45，ε＝0.001，G＝0.1时单个神经元产生混沌簇放电活动.式（2）中cintra代表子网络内的耦合强度，cinter代表子网络间的耦合强度，gI，J＝（gI，J（i，j））表示连接矩阵，如果第I个子网络中的第i个神经元与第J个子网络中的第j个神经元相连，则有gI，J（i，j）＝gJ，I（j，i）＝1，否则gI，J（i，j）＝gJ，I（j，i）＝0.式（2）中wI＝（wI（i，j））表示第I个子网络中的连接矩阵，如果第I个子网络中的第i个神经元与第j个神经元相连，则有wI（i，j）＝wI（j，i）＝1，否则wI（i，j）＝wI（j，i）＝0且wI（i，i）＝0.化学耦合项中的S（x，θ）＝H（x-θ）是阶梯函数，当突触前神经元的膜电位x超过突触阈值θ时对突触后神经元产生作用.式（2）中τ是突触传递的时间延迟，vexc是突触可逆电位.在以下研究中，设定cinter＝0.01，θ＝0.45，vexc＝0.6.

1.2 簇同步指标

本文通过计算序参数R［21］来定量刻画模块网络中神经元簇放电的同步程度，其定义式为：

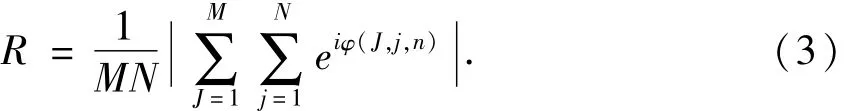
这里φ（J，j，n）表示第J个子网络中的第j个神经元在时刻n处的簇放电相位，表达式为：

其中，nJ，j，k是第J个子网络中第j个神经元的第k个簇开始放电的时刻.R的值越大，表明模块神经元网络簇同步程度越强.当模块神经元网络中所有神经元簇放电达到同步时，簇相位几乎一致，从而R接近于1.当网络中所有神经元处于完全不同步状态时，簇相位几乎不相关，从而R≈0.考虑到网络结构的随机性，以下关于R的数值计算结果是对网络结构平均50次的结果.

模块神经元网络中神经元簇放电的同步程度还可以用平均场X来定性描述，具体为.当模块神经元网络中所有的神经元以相同的节律放电时，平均场序列呈现出类似周期的大幅振荡；而当模块神经元网络中所有的神经元都以各自节律放电时，平均场序列表现出近似随机的小幅振荡.

2 模块神经元网络的簇同步动力学特性

在这一部分，我们首先讨论当模块神经元网络中不含时滞（即τ＝0）时，子网络内耦合强度对模块神经元网络簇同步的影响.然后，在耦合项中引入时滞，进一步探究时滞对模块神经元网络簇同步的影响.

2.1 耦合强度诱导的簇同步

为了研究子网络内耦合强度对模块神经元网络簇同步的影响，在下面的讨论中，固定子网络间的连接概率和耦合时滞分别为pinter＝0.02和τ＝0.

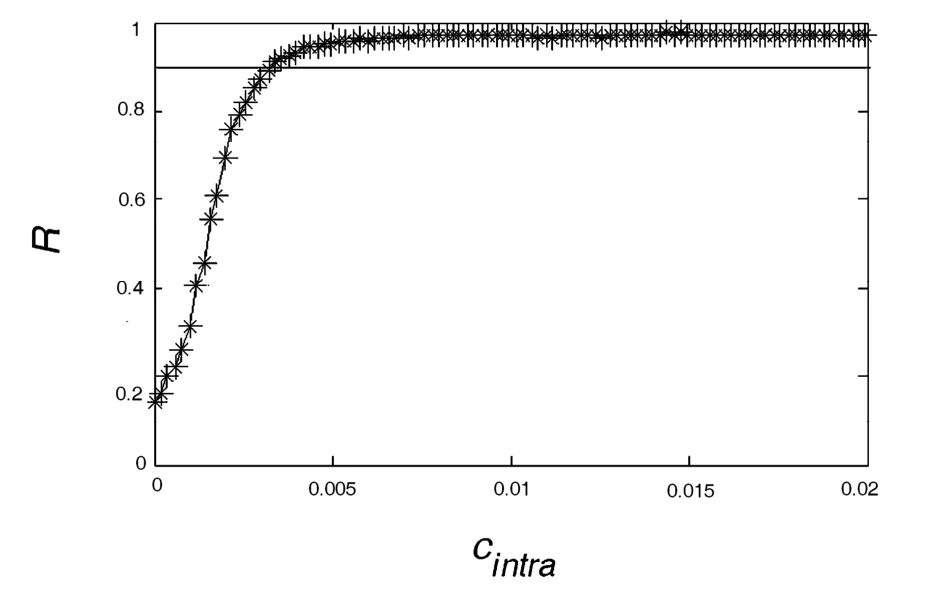
图1 当pinter＝0.02时，序参数R随子网络内耦合强度cintra的变化Fig.1 Relationship of the order parameter R and the intra-coupling strength cintrawhen pinter＝0.02

图1描述了序参数R随着子网络内耦合强度cintra的变化趋势.从图中可以观察到，随着耦合强度的增大，序参数R也随之变大，且当cintra超过某一临界值ccritical≈0.0035时，序参数R大于0.9.这表明模块神经元网络在较强的子网络内耦合强度的作用下能够取得簇同步（本文模型验证了当R＝0.9时，模块神经元网络能够达到较好的簇同步状态）.这种现象也可以通过其他方式如网络的时空图和平均场来形象刻画.图2分别展示了当耦合强度小于临界值和大于临界值时网络的时空图和平均场序列.当子网络内的耦合强度小于簇同步的临界值时（如cintra＝0.001），模块神经元网络中神经元的放电节律不一致，其时空图呈现混乱状态（图2（a）），此时平均场也表现出小幅的随机波动（图2（c））；这表明较弱的耦合强度不足以使模块神经元网络达到簇同步.相反地，当子网络内的耦合强度大于簇同步的临界值时（如cintra＝0.01），模块神经元网络中神经元的放电节律基本一致，其时空图呈现出较规则状态（图2（b）），此时平均场序列出现类似周期的大幅振荡（图2（d）），这表明较强的耦合强度可以使模块神经元网络达到簇同步.

图2 当pinter＝0.02时，不同子网络内耦合强度取值下的时空图和平均场X随时间的演化曲线（a）cintra＝0.001；（b）cintra＝0.01；（c）cintra＝0.001；（d）cintra＝0.01Fig.2 Space-time plots and time history of themean field X for different cintraofmodular neuronal network when pinter＝0.02（a）cintra＝0.001；（b）cintra＝0.01；（c）cintra＝0.001；（d）cintra＝0.01

2.2 时滞诱导的簇同步转迁

为研究时滞对模块神经元网络簇同步的影响，不失一般性，设子网络内的耦合强度为cintra＝0.005.图3刻画了不同时滞τ作用下模块神经元网络的时空图.从图中可以观察出，随着时滞的增大，模块神经元网络的时空图间歇地呈现出规则与不规则的状态，这表明了时滞对模块神经元网络的簇同步行为有着重要影响.在没有时滞（τ＝0）的情况下，模块神经元网络中所有神经元的放电节律基本一致，模块神经元网络达到了簇同步状态，如图3（a）所示；当时滞τ＝200时，模块神经元网络中神经元的放电节律变得十分混乱，模块神经元网络簇同步状态遭到破坏（见图3（b））；当时滞增大到τ＝380时，模块神经元网络又出现簇同步状态，如图3（c）所示；随着时滞的进一步增大，模块神经元网络的簇同步状态在τ＝570时又消失，而在τ＝750时再次出现（见图3（d）和3（e））；类似的现象在τ＝940，τ＝1120，τ＝1330和τ＝1490处再次重复出现，如图3（f）-3（i）所示.以上现象表明合适的时滞可以诱导、也可以破坏模块神经元网络的簇同步行为，即随着耦合时滞的增大模块神经元网络的簇同步状态和非同步状态能够间歇性出现.

图3 当pinter＝0.02，cintra＝0.005时，不同时滞τ作用下模块神经网络的时空图（a）τ＝0；（b）τ＝200；（c）τ＝380；（d）τ＝570；（e）τ＝750；（f）τ＝940；（g）τ＝1120；（h）τ＝1330；（i）τ＝1490Fig.3 Space-time plots ofmodular neuronal network for different delaysτwhen pinter＝0.02 and cintra＝0.005（a）τ＝0；（b）τ＝200；（c）τ＝380；（d）τ＝570；（e）τ＝750；（f）τ＝940；（g）τ＝1120；（h）τ＝1330；（i）τ＝1490

为了进一步研究耦合时滞对模块神经元网络簇同步的影响，图4（a）描述了序参数R随时滞τ的演化曲线.从图中可以观察到，随着时滞τ的增大，曲线呈现出多个极大值和极小值交替出现的现象.序参数R的极大值大约出现在τ＝380，τ＝750，τ＝1120，τ＝1490处，且序参数R的这些极大值都大于0.9.这表明此时模块神经元网络具有较好的簇同步状.序参数R的极小值大约出现在τ＝200，τ＝570，τ＝940，τ＝1330处，且序参数R的这些极小值都接近0，这表明此时模块神经元网络处于非同步状态.这些结果与图3中时空图的分析结果一致，即适当的时滞可以使得模块神经元网络的簇同步活动发生间歇性转迁.

为了探索耦合时滞诱导的模块神经元网络簇同步转迁的动力学机理，图4（b）刻画了模块神经元网络中所有神经元平均膜电位的时间演化曲线.标记图中簇与簇之间的时间间隔依次为Ti（i＝1，2，…），假设在一段时间内有L个簇出现，记网络中所有神经元的平均振荡周期为，经计算得T≈380.可见，能够使得模块神经元网络簇同步间歇出现的耦合时滞大约是网络平均振荡周期T的整数倍.所以，模块神经元网络发生簇同步转迁是由于耦合时滞与网络平均振荡周期的相锁而引起的.

图4 当pinter＝0.02，cintra＝0.005时，（a）序参数R随时滞τ变化的曲线；（b）模块神经元网络中所有神经元的平均膜电位的时间演化曲线Fig.4 （a）Order parameter R-delayτcurves；（b）Time evolution of the averagemembrane potential of all the neurons in modular network when pinter＝0.02 and cintra＝0.005

2.3 时滞诱导的簇同步转迁对其他参数的鲁棒性

首先研究子网络间的连接概率对模块神经元网络簇同步转迁的影响.图5给出了序参数R随时滞τ和子网络间连接概率pinter变化的投影图.从图中可以观察出，对于不同的子网络间连接概率，随着时滞τ的逐渐增大，模块神经元网络的簇同步和非同步区域交替出现，而且诱导簇同步间歇出现的耦合时滞没有随着pinter的改变而发生显著性变化.这表明时滞诱导的簇同步转迁对模块神经元网络子网络间的连接概率具有鲁棒性.

接下来研究子网络内的耦合强度对模块神经元网络簇同步转迁的影响.图6描述的是序参数R随时滞τ和子网络内耦合强度cintra变化的投影图.从图中可以观察出，当子网络内的耦合强度超过某一临界值后，对于不同的子网络内耦合强度，随着时滞τ的逐渐增大，模块神经元网络的簇同步和非同步区域交替出现，而且诱导簇同步间歇出现的耦合时滞没有随着cintra的改变而显著性变化.这表明时滞诱导的簇同步转迁对模块神经元网络子网络内的耦合强度具有鲁棒性.

图5 当cintra＝0.005时，序参数R随时滞τ和子网络间连接概率pinter变化的投影图Fig.5 The contour plot of order parameter R over the plane of τand pinterwhen cintra＝0.005

图6 当pinter＝0.02时，序参数R随时滞τ和子网络内的耦合强度cintra变化的投影图Fig.6 The contour plot of order parameter Rover the plane of τand cintrawhen pinter＝0.02

如引言所述，耦合时滞在神经元网络中普遍存在.由于神经元间信息传导速度从20m/s到60m/s，从而引起的传导时滞是从几毫秒到几百毫秒［22］，这与本文所讨论的耦合时滞范围相一致.文中研究结果表明适当的耦合时滞可以使得模块神经元网络的簇同步活动发生间歇性转迁，特别是耦合时滞对簇同步的抑制作用，这对一些神经疾病（如癫痫和帕金森病症）等的动力学控制提供理论指导意义.当改变网络规模时，如子网络节点个数增多或者子网络节点个数不等，本文所得的结果依然成立.限于篇幅，这里不再列举.

3 总结

耦合时滞在模块神经元网络中普遍存在.本文通过构建子网络是NW小世界网络的模块神经元网络，研究了耦合时滞作用下模块神经元网络的簇同步动力学.研究结果表明，较强的子网络内耦合强度可以诱导模块神经元网络达到簇同步.同时，当耦合项中引入时滞后，发现当时滞大小约为网络中所有神经元平均振荡周期的整数倍数时，时滞可以诱导模块神经元网络的簇同步发生间歇性转迁，并且时滞诱导的簇同步转迁对子网络内的耦合强度、子网络间的连接概率具有鲁棒性.

1 Singer W.Synchronization of cortical activity and its putative role in information processing and learning.Annual Review of Physiology，1993，55（55）：349～374

2 Franovic I，Miljkovic V.Phase plane approach to cooperative rhythms in neuronmotifswith delayed inhibitory synapses.Europhysics Letters，2010，92（6）：1637～1649

3 Belykh I，Lange E D，Hasler M.Synchronization of bursting neurons：what matters in the network topology.Physical Review Letters，2005，94（18）：188101

4 Dhamala M，Jirsa V K，Ding M Z.Transitions to synchrony in coupled bursting neurons.Physical Review Letters，2004，92（2）：028101

5 Zheng Y H，Lu Q S.Spatiotemporal patterns and chaotic burst synchronization in a small-world neuronal network. Physica A，2008，387（14）：3719～3728

6 Han F，Lu Q S，Wiercigroch M，et al.Chaotic burst synchronization in heterogeneous small-world neuronal network with noise.International Journal of Non-Linear Mechanics，2009，44（3）：298～303

7 Buric N，Todorovc K，Vasovic N.Synchronization of bursting neurons with delayed chemical synapses.Physical Review E，2008，78（3-2）：417～423

8 Han F，Lu Q S，Wiercigroch M，et al.Complete and phase synchronization in a heterogeneous small-world neuronal network.Chinese Physics B，2009，18（2）：482～488

9 Wang Q Y，Perc M，Duan ZS，etal.Synchronization transitions on scale-free neuronal networks due to finite information transmission delays.Physical Review E，2009，80（2）：1711～1715

10 Jalili M.Phase synchronizing in Hindmarsh-Rose neural networks with delayed chemical coupling.Neurocomputing，2011，74（10）：1551～1556

11 Hilgetag C C，Kaiser M.Clustered organisation of cortical connectivity.Neuroinformatics，2004，2（3）：353～360

12 Huang L，Lai Y C，Gatenby R A.Alternating synchronizability of complex clustered networks with regular local structure.Physical Review E，2008，77（1-2）：119～136

13 Lopez G Z，Zhou C S，Kurths J.Exploring brain function from anatomical connectivity.Frontiers in Neuroscience，2011，5：1～4

14 Batista C A S，Lameu E L，Batista A M，et al.Phase synchronization of bursting neurons in clustered small-worldnetworks.Physical Review E，2012，86（1）：1411～1432

15胡丽萍，杨晓丽，孙中奎.混合突触作用下耦合时滞对模块神经元网络簇同步的影响.动力学与控制学报，2015，13（6）：462～467（Hu L P，Yang X L，Sun Z K. Effect of coupled time-delay on bursting synchronization in modular neuronal network with hybrid synapses.Journal of Dynamics and Control，2015，13（6）：462～467（in Chinese））

16 Jia Y B，Yang X L，Kurths J.Diversity and time delays induce resonance in a modular neuronal network.Chaos，2014，24（4）：043140

17 Liu C，Wang J，Yu H T，et al.Impact of delays on the synchronization transitions of modular neuronal networks with hybrid synapses.Chaos，2013，23（3）：539～552

18 Newman M E，Watts D J.Scaling and percolation in the small-world network model.Physical Review E，2000，60（6）：7332～7342

19 Courbage M，Nekorkin V I，Vdovin L V.Chaotic oscillations in a map-based model of neural activity.Chaos，2007，17（4）：155～160

20 Courbage M，Nekorkin V I.Map basedmodels in neurodynamics.International Journal of Bifurcation and Chaos，2010，20（6）：1631～1651

21 Ivanchenko M V，Osipov G V，Shalfeev V D，et al.Phase Synchronization in Ensembles of Bursting Oscillators. Physical Review Letters，2004，93（13）：134101

22 Kandel E R，Schwartz JH，Jessell TM.Principles of Neural Science.New York：Elsevier，1991

COUPLING DELAY-INDUCED BURST SYNCHRONIZATION TRANSITIONS IN A MODULAR NEURONAL NETWORK*

Wang Manman Yang Xiaoli†
（College of Mathematics and Information Science，Shaanxi Normal University，Xi′an 710062，China）

Through constructing a model of delay-coupled modular neuronal network by Courbage-Nekorkin-Vdovin neuron elements，this paper numerically studies the effect of coupling strength and delay on the firing properties of burst synchronization.The results show that appropriately large coupling strength can induce burst synchronization in thismodular neuronal network.At the same time，it is found that coupling delay can induce the transitions of burst synchronization for themodular neuronal network.Moreover，all these transitions of burst synchronization occur approximately when the value of the delay approximately equates to the integermultiples of average oscillation period for all the neurons in themodular neuronal network.Additionally，delay-induced burst synchronization transitions are confirmed to be robust to the intra-coupling strength and the inter-connection probability in themodular neuronal network.

modular neuronal network， coupling delay， burst synchronization transitions

10.6052/1672-6553-2016-012

2015-12-17收到第1稿，2016-01-31收到修改稿.

*国家自然科学基金资助项目（11572180），陕西省自然科学基础研究计划项目（2014JQ1013），中央高校基本科研业务费专项基金（GK201302001）资助课题

†通讯作者E-mail：yangxiaoli＠snnu.edu.cn

Received 17 December 2015，revised 31 January 2016.

*The project supported by the National Natural Science Foundation of China（11572180），the NSF of Shaanxi Province（2014JQ1013）and the Fundamental Funds Research for the Central Universities（GK201302001）

†Corresponding author E-mail：yangxiaoli＠snnu.edu.cn