带有弹性联轴器的齿轮传动系统随机非线性分析

付宗涛温建明

（同济大学航空航天与力学学院，上海 200092）

带有弹性联轴器的齿轮传动系统随机非线性分析

付宗涛†温建明

（同济大学航空航天与力学学院，上海 200092）

带有弹性联轴器的齿轮传动系统中，弹性联轴器的非线性恢复力函数和阻尼力函数均是频率和振幅的函数，在受到随机激励作用下形成了一类非线性随机系统.文中应用基于高斯勒让德积分的路径积分法计算此传动系统的位移-速度概率密度，并给出一些特定时刻的概率密度分布.最后，分析边界外概率丢失的问题，提出相应的解决方案.

路径积分法， 高斯勒让德积分， 高斯激励， 迹法， 概率丢失

引言

在研究随机动力学系统时，常借助FPK方程.受高斯白噪声激励的线性或非线性动力学系统的响应可用Markov过程描述，而响应的转移概率密度则由FPK方程所确定［1］.实际上，只有少数特殊的FPK方程才能得到其精确平稳解［2］.常用的近似方法主要有随机平均法、正交函数展开法等，但是它们不能完全适用于本质非线性，因此如何构造高效地求解适用于本质非线性的FPK方程的数值方法备受关注.目前，求解FPK方程的数值方法包括有限元法、路径积分法、变分法等［3-4］.

路径积分法是最早由Feynman提出的用于解决量子力学问题的一种新的泛函积分表述.路径积分的基本思想是在空间和时间上分别离散化，以路径和代替积分，即通过连接短时转移概率密度形成全局转移概率密度，得到状态向量的联合概率密度函数.Wehner和Wolfer［5］最早提出基于路径积分的数值方法来求解具有自然边界条件的FPK方程.Yu等［6］提出了基于高斯勒让德公式的路径积分法，提高了概率密度计算精度.路径积分法在非线性随机动力学系统研究中得到大量应用.Yim和Lin［7］计算了甲板上浪作用下的船舶倾覆模型的概率密度，并借助概率密度分析了混沌运动.王迎光和谭家华［8］利用基于隐式高斯勒让德插值的路径积分法计算了一强非线性随机动力系统的响应统计.

本文基于已有的实验研究成果［9］，对带有弹性联轴器的齿轮传动系统进行随机响应研究.在确定性系统中，联轴器的恢复力是基于迹法模型拟合而得，是位移的三次函数，一次项和三次项的系数均是振幅和频率的函数；阻尼力是基于能量损耗相等的线性阻尼而得，是速度的一次函数，其系数也是振幅和频率的函数.在研究随机非线性系统时，仍然采用这种模型，只在外激励项中添加随机成分.由于随机非线性系统的复杂性，在研究过程中采用了一些简化措施，将随机非线性模型中位移和速度的系数根据确定性系统的模型转变为常数.本文得到此传动系统的位移-速度概率密度，并给出了一些特定时刻的概率密度分布.最后，分析边界外概率丢失的问题，提出相应的解决方案.

1 两转子轴系传动系统

1.1 确定性系统的动力学方程

针对两转子轴系来建立动力方程，设主动端（功率输入端）的等效转动惯量J1，在稳定运动下以角位移x1＝ω1t+a0cos（ωt），经联轴器带动从动端（J2），橡胶弹性元件的压缩量为x，则从动端转角为x2＝x1-x，从动端受阻力为M2.对转子J2有动力学方程

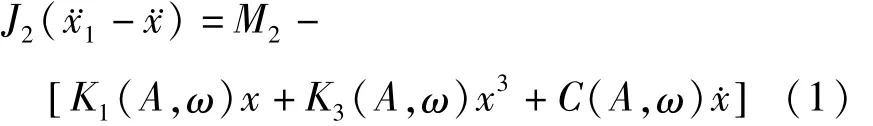
其中，A是振幅，ω是外激励频率，

整理得

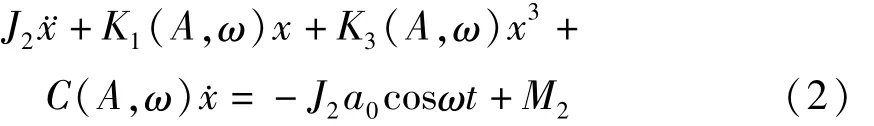
考虑上式右端为单频激励的情况，即假设M2为ω角频率的周期激励.不妨设上式右端为M′0cos（ωt），得到

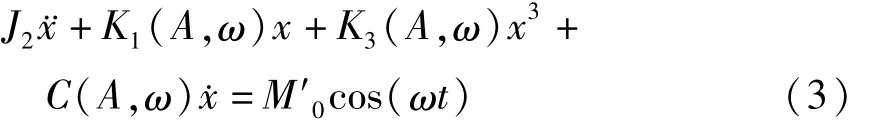
上式即为联轴器两转子轴系确定性系统的动力学方程.

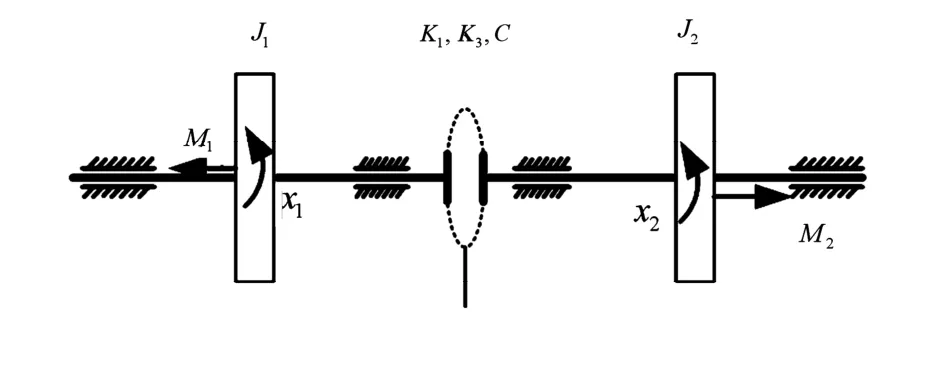
图1 弹性联轴器联结的两转子轴系示意图Fig.1 Diagram of double rotor shafting system with flexible couplings

1.2 随机系统的动力学方程

针对式（3），假设右端附加强度为σ的高斯白噪声激励

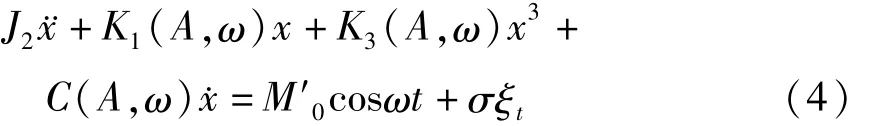
其中ξt是单位功率高斯白噪声.上式即为联轴器两转子轴系受随机激励的动力学方程.需要注意的是，式（4）中的K1，K3，C均是式（3）确定性系统中的值.

2 随机系统的响应统计量求解

式（4）是一个谐和激励与高斯白噪声激励作用下的非线性Duffing-Rayleigh振子，它的响应统计量可以利用路径积分法进行求解，求解过程计算量较小，结果的精度较高［10］.

2.1 Duffing-Rayleigh振子的路径积分解

考虑如下谐和激励与高斯白噪声激励作用下的非线性Duffing-Rayleigh振子

其中ω1是固有频率，γ是线性阻尼系数，β和ε是非线性参数，σ1和ω分别表示正弦激励的强度和频率，白噪声ξt的强度为σ2.相应地导出响应的转移概率密度Q的FPK方程

其中mij＝E［xi˙xj］（i，j＝0，1，2）.对于二维情形，随机动力学系统的短时转移概率密度表达式为

其中，

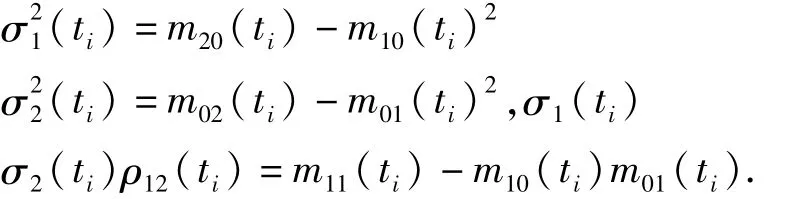
对于概率密度的二维二点高斯积分，在已知第（i-1）时刻的每个高斯积分点处的概率密度及相应的转移概率密度时，借助离散化的概率密度表达式可得第i时刻任意点处的概率密度：

其中，m＝1，2，…，K，n＝1，2，…，Lk，K是子区间数，Lk是第k子区间的高斯积分点数，此处为4，Ak是第k子区间的面积，xkl是高斯积分点，ckl是相应的权重.

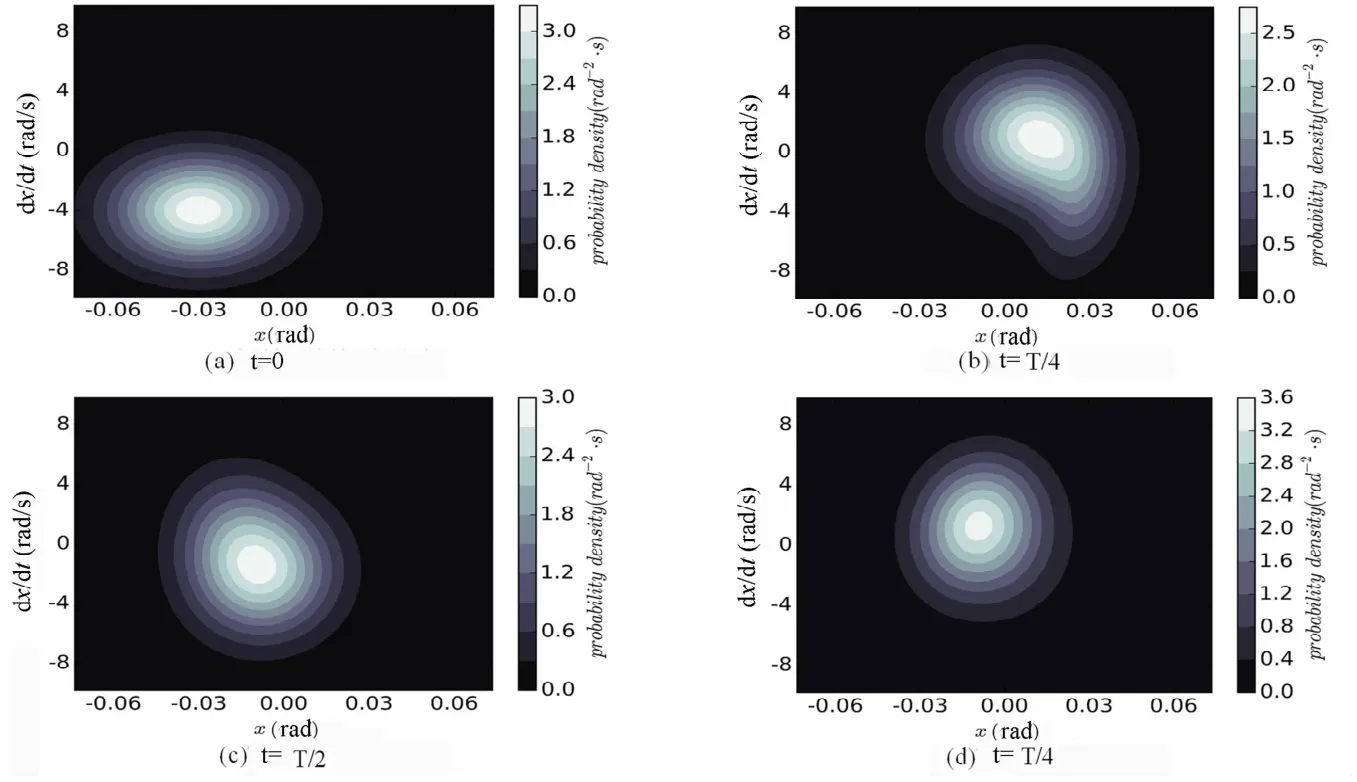
图2 瞬态概率分布Fig.2 Distribution of transient probability

2.2 传动系统速度-位移概率密度的路径积分解

根据已有的确定性系统实验数据［9］，对于式（4），取J2＝0.25N·m·s2，M′0＝80N·m，ω＝94.25，A＝1.778×10-2，σ＝13.将刚度系数和阻尼系数处理为对应的确定性系统的数值，那么K1＝4.66×103，K3＝3.16×107，C＝145.11.考察位移的范围为-0.075～0.075（rad），速度的范围为-10～10（rad/s），并分割为50×50个子区间，子区间内为二维二点高斯积分，时间步长Δt＝T/4.初始分布为

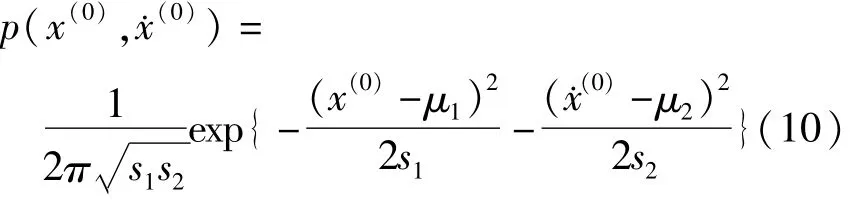
其中，μ1＝-0.03，μ2＝-4，s1＝0.0004，s2＝6.

图3 稳态概率分布（第26个周期）Fig.3 Distribution of stationary probability（the 26thcycle）

通过利用式（7）（8）（9），可以得到时间步长为T/4的所有时刻的概率密度.图2、图3表明本系统是单峰稳定的，不具有多稳定周期解情况下的响应跳跃现象.

2.3 概率丢失问题及修正方法

对于式（9），由于并不是［-∞，∞］×［-∞，∞］的全范围积分，而是［-0.075，0.075］×［-10，10］区域范围内的高斯勒让德积分，区域外的概率丢失，故每迭代求解一次概率密度，区间内总体概率都会减小.对于图2（a），区域内概率为0.9808；对于图3（d），区域内概率为0.8135.可见，概率损失比较严重.如果选择更大的区间，为了保持精度，需要划分更多网格，计算量大.考虑到本系统是稳定的，区域外的概率会回归到区域内，将子区间高斯积分点及中心的概率密度作如下简单修正处理：

其中，脚标c表示区间内高斯积分点或者中心，以区别式（9）中的脚标l.修正后的稳态概率分布见于图4（a），对应图3（d）时刻.为了考察修正前后概率分布形状的变化，采用指标diff作为参考标准.

图4 修正处理对概率分布的影响Fig.4 The influence of improvement on the probability distribution

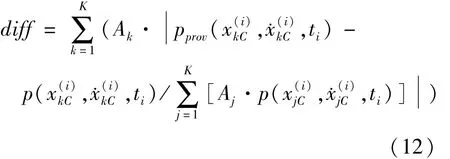
其中，脚标prov表示修正后，脚标C表示子区间中心.diff计算的结果为1.3533×10-11，具体到每个子区间的相差分布见于图4（b）.可见，修正措施对概率分布的形状影响极小，是一种可行的方案.需要强调的是，这种修正适合所选区域范围包含全部稳定点的情况，否则将得到错误的概率分布.

3 结论

本文根据已有弹性联轴器扭振实验的实验结果和基于迹法的联轴器动力学模型，建立了由弹性联轴器联结的两转子轴系齿轮传动系统的随机动力学模型.针对该模型，采用基于高斯勒让德积分的路径积分法计算速度和位移的响应统计，给出了瞬态和稳态的部分时刻的位移-速度概率分布.最后，本文分析了边界外概率丢失的问题，提出相应的修正方案，并对比修正前后稳态概率分布形状，发现修正对概率分布形状影响极小，说明了修正方案的合理性.

1 邵耀椿，封国林，李俊来.Fokker-Planck方程.昆明理工大学学报，1996，21（3）：18～21（Shao Y C，Feng G L，Lin JL.Fokker-Planck equation.Journal of Kunming University of Science and Technology，1996，21（3）：18～21（in Chinese））

2 Lin Y K，CaiG Q.Probabilistic Structural Dynamics：Advanced Theory and Application.New York：McGraw-Hill，1995

3 Dunne JF，GhanbariM.Extreme-value prediction for nonlinear stochastic oscillators via numerical solutions of the stationary FPK equation.Journal of Sound and Vibration，1997，206（5）：697～724

4 张丽强.高维FPK方程的数值解法.杭州：浙江大学出版社，2006（Zhang L Q.Numerical solutions for high-dimensional FPK equation.Hangzhou：Zhejiang University Publishing，2006）

5 Wehner M F，Wolfer GW.Numerical evaluation of pathintegral solutions to Fokker-Planck equations.Physical Review A，1983，27（5）：2663～2670

6 Yu JS，Lin Y K.Numerical path integration of a nonlinear oscillator subject to both sinusoidal and white noise excitations∥Advances in Stochastic Structural Dynamics.Boca Raton，FL，USA：CRC Press，2003

7 Yim SC S，Lin H.Unified analysis of complex nonlinear motion via densities.Nonlinear Dynamics，2001，24（1）：103～127

8 王迎光，谭家华.一强非线性随机震荡系统的路径积分解.振动与冲击，2007，26（11）：153～162（Wang Y G，Tan JH.Path integral solution of a strongly nonlinear stochastic oscillation system.Journal of Vibration and Shock，2007，26（11）：153～162（in Chinese））

9 付宗涛，温建明.齿式橡胶联轴器大位移扭振实验与建模.石家庄铁道大学学报（自然科学版），2016，29（1）：80～85（Fu Z T，Wen JM.Large displacement torsional vibration experiments of a gear rubber coupling.Journal of Shijiazhuang Tiedao University（Natural Science Edition），2016，29（1）：80～85（in Chinese））

10徐伟.非线性随机动力学的若干数值方法及应用.北京：科学出版社，2013（Xu W.Numerical Analysis Methods for Stochastic Dynamical System.Beijing：Science Press，2013（in Chinese） ）

RESEARCH ON STOCHASTIC NONLINEAR BEHAVIOR OF A GEAR SYSTEM W ITH FLEXIBLE COUPLINGS

Fu Zongtao†Wen Jianming
（School of Aerospace Engineering and Applied Mechanics，Tongji University，No.1239 Siping Road，Shanghai 200092，China）

For the gear system with flexible couplings，the nonlinear elastic force and damping force are both the functions of displacement and velocity.A nonlinear stochastic system is generated under the excitation of stochastic force.The path integralmethod based on Gauss-Legendre integral is applied to calculate the joint probability density of displacement and velocity responses.Moreover，the distributions of probability density at some special time points are given.In the end，the problem of probability loss is analyzed，and a feasiblemeasure to dealwith it is also put forward.

path integralmethod， Gauss-Legendre integral， Gauss white noise excitation， polynomial approximation， probability loss

10.6052/1672-6553-2016-005

2015-08-24收到第1稿，2015-12-16收到修改稿.

†通讯作者E-mail：1334014＠tongji.edu.cn

Received 24 August2015，revised 16 December 2015.

†Corresponding author E-mail：1334014＠tongji.edu.cn