基于变参数环板等效叶片组的叶盘模型耦合振动分析方法*

姜萌 张美艳 唐国安

（复旦大学航空航天系，上海 200433）

基于变参数环板等效叶片组的叶盘模型耦合振动分析方法*

姜萌 张美艳 唐国安†

（复旦大学航空航天系，上海 200433）

转子系统常见于旋转机械装置中，在航空、电力、化工等工业和民用的诸多行业中发挥着重要作用.转子系统一般由轴和多级叶轮组成，存在强度、疲劳、振动和噪声等一系列问题，亟待通过优化设计等手段提高产品的各项性能.由于每级叶轮都含有由多条叶片构成的叶片组，因此在应用有限元等方法分析时，即便利用了回转周期的性质，转子系统的整体自由度数目依然庞大，优化设计的计算效率有待提高.为了提高转子系统分析的效率，可将根据气动性能要求设计的单级叶盘视为状态已经确定的子系统，在具备足够计算精度的前提下对其有限元模型进行缩聚或简化，以降低整体系统的自由度.文章介绍叶片组模型的等效建模方法，以固有振动特性相近为等效准则，将有限元模型中周向环绕的叶片组等效为变参数圆柱型正交各向异性环形板，并通过理论推导和计算得到了环板模型的几何与材料等物理参数.以航空发动机低压涡轮叶盘模型为例，实现了叶片组的模型等效过程.结果表明，等效方法可在保证精度的前提下大大降低模型的自由度数目，为后续整体转子系统的优化设计提供了高效的叶盘建模方法.

振动， 叶片， 轮盘， 转子， 模型缩聚

引言

燃气发动机、叶轮发电机、空气压缩机以及牙科高速手机等以转子为核心部件的旋转机械广泛应用于工业和民用各个领域，在经济和生活中发挥着重要的作用.从经典的两端简支、带刚性圆盘弹性转轴的Jeffcott转子［1］，到带多个刚性圆盘的多轴转子系统［2］，转子动力学的研究长期受到学者的关注.对于高转速的转子，张文［3］指出不能再将叶盘视为刚性部件，而应当将其作为弹性体，建立柔盘-柔轴的全弹性转子模型进行处理.但是，在工程应用时，若叶-盘-轴全部部件都采用有限元模型描述，那么整体转子系统的自由度将十分庞大，转子动力学计算难以实施.大幅度降低单级弹性叶盘模型的自由度是高效分析全弹性转子的必要步骤.

早期一些学者提出过基于简化单条叶片的叶盘模型分析方法，如Ewins［4］，Kaza和Kielb［5］等将叶片等效为弹性梁模型，Genta［6］提出将叶片模化成单摆结构，并进一步分析叶盘系统的耦合振动特性.后来的学者，如Omprakash［7］，王文亮［8］，张文［9］，白斌和白广忱［10］等，利用叶盘的回转周期特性、结合动态子结构等方法，提出了一系列基于扇区的叶盘有限元模型缩聚算法，大大提高了弹性叶盘振动分析的效率.概括地说，基于简化单条叶片的叶盘简化模型，形式直观适合工程应用，便于多个叶盘与转轴的组装，但精度相对较低.基于扇区的叶盘缩聚模型精度很高，但难以与通用转子动力学分析软件衔接，且对于形状复杂的叶盘，一个扇区有限元模型的节点数很多，缩聚后模型的自由度依旧很高.

在含有多级叶盘的全弹性转子系统中，建立具有足够精度、便于与通用有限元程序衔接的低自由度叶盘模型，对于整体转子动力学分析和优化设计仍具有重要意义.以此为目的，本文根据周向环绕的单级叶片组的物理参数和模态分析结果，将其等效为固有振动特性相近的正交异性环形板.在此基础上，将叶片组的等效环形板与轮盘对接后便可构成简单、有效的单级叶盘缩聚模型，为多级、全弹性转子系统的动力学高效分析奠定了基础.

1 等效叶片组的变参数环板模型

图1所示是叶盘的初始模型，由轮盘、叶片组和叶冠三部分构成.图2为图1对应的叶盘缩聚模型.在缩聚模型中，轴对称轮盘和叶冠两部分保持不变，周向环绕的叶片组被等效为变参数环形平板，其材料本构特性为极坐标系下的正交各向异性，密度假设为沿径向呈线性变化.从动力学角度考虑，模型等效应当满足条件：

①叶片组与环板的质量和转动惯量相同；

②带冠叶片组与带冠环板的动力学特性（固有频率和模态）相近.

记初始叶片组总质量为Mb，绕横轴惯性矩为Ib，材料密度为ρb，内外缘的半径分别是R0和R1，均为初始模型的已知参数.

图1 叶盘的初始模型Fig.1 Initialmodel of bladed disk

图2 叶盘缩聚模型Fig.2 Reduced model of bladed disk

建立等效模型时，环板的内、外半径分别取为R0和R1，体积与叶片组相同（即Mb/ρb），那么环板厚度为

环板的质量密度沿径向呈线性变化的关系可表示为

其中，ρ0和ρ1是环板内外缘的待定密度值.

根据质量密度的分布函数（2），积分后可得环板质量和转动惯量分别为

利用公式（3）和（4），根据叶片组等效前后质量和转动惯量相等的条件①，即，可建立

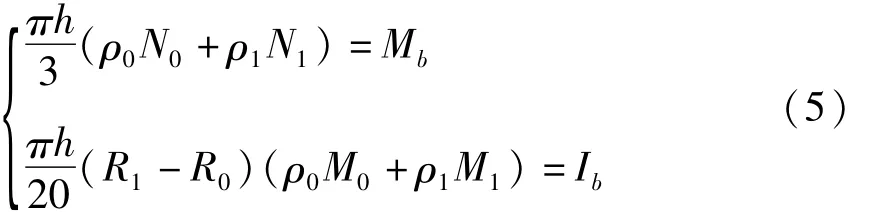
求解方程组（5）可确定（2）中的环板内外缘质量密度值ρ0和ρ1，亦即确定了密度分布函数＾ρ（r）.

极坐标系下正交各向异性材料含有5个弹性系数，分别为杨氏模量Er和Eθ，剪切模量Grθ，以及泊松系数μr和μθ.但由于存在对称关系μθ/Eθ＝μr/Er，因此只有4个弹性系数是独立的.

带冠环板和带冠叶片组的第j阶固有频率ωj和＾ωj应当近似相等，即条件②可表示为非线性规划的极小化问题

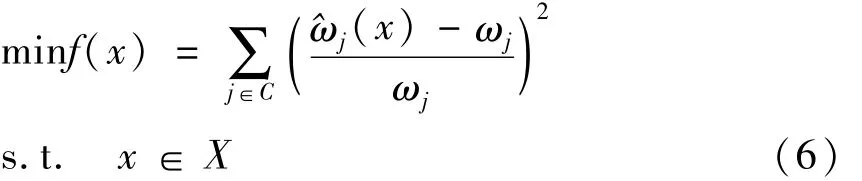
2 带叶冠环板的弹性参数估算

目标函数f（x）是非线性的，极小化问题（6）可能存在多个局部解.选取不同设计变量的初值，可能会得到不同的极小化结果.只有给出尽可能接近真实解的设计变量初值，才能得到合理的环板弹性常数.对于变参数正交各向异性带冠环板，本文采用基于动能和势能表达式的Rayleigh法，导出带冠环板固有频率的解析式，进而给出确定环板弹性常数初值的方法.

2.1 环板动能和势能表达式

等效后带冠环板如图3所示，以环板中心为原点、法向为x轴，建立极坐标系O-rθx.根据薄板弯曲理论［11］，板的横向振动模态可以用中面x方向的位移函数Ux（r，θ）表示.函数Ux（r，θ）则可根据周向变化的周期数分类，表示为

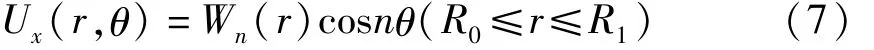
其中n称为模态的节径数.

记Dr，Dθ分别是环板在r，θ方向上的抗弯刚度，Dk为抗扭刚度，则n节径振动的环板弹性势能［12］和动能分别为

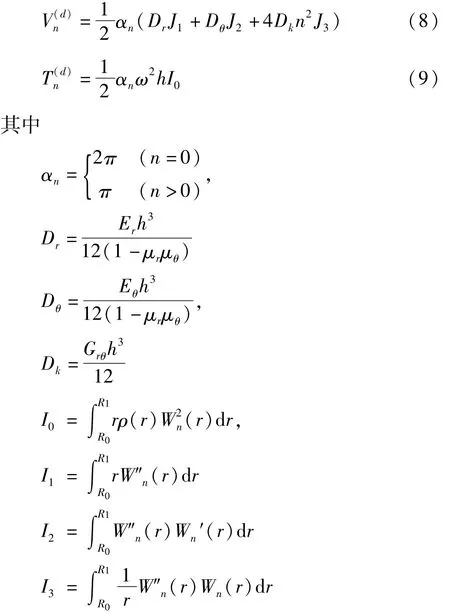
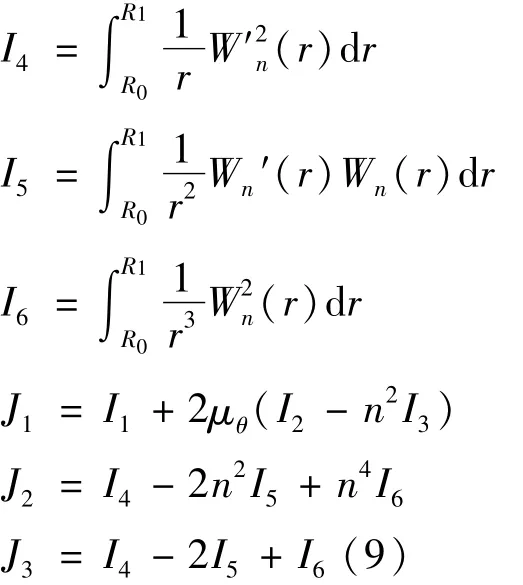
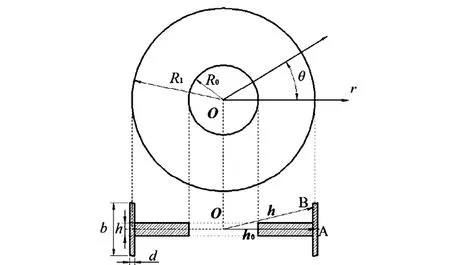
图3 带冠环板模型示意图Fig.3 Sketch of circular plate with shroud

2.2 叶冠动能和势能表达式

叶冠的变形由环板带动，环板外缘绕r，θ和x轴的转角分别是

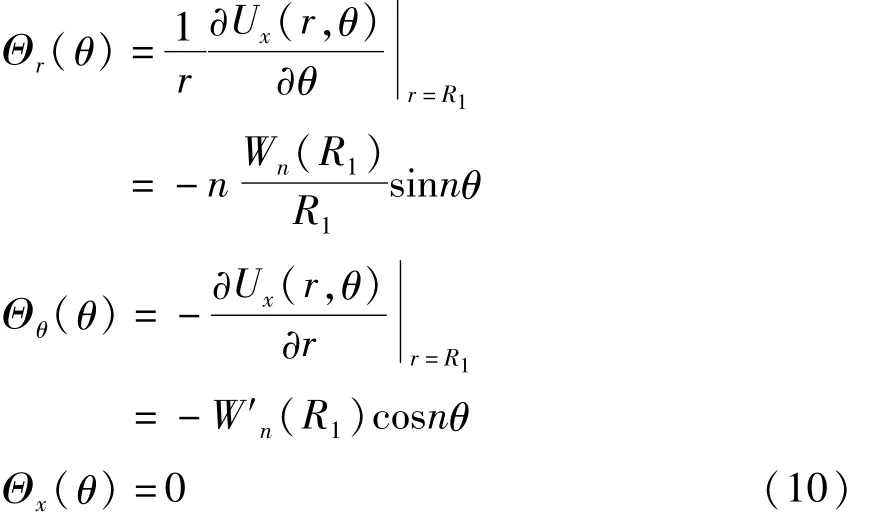
记叶冠上任意点B、叶冠中心与叶片相连点A关于坐标原点的矢径分别为h和h0，则B点的位移可近似表达为A点的牵连运动以及关于A点的相对运动的叠加

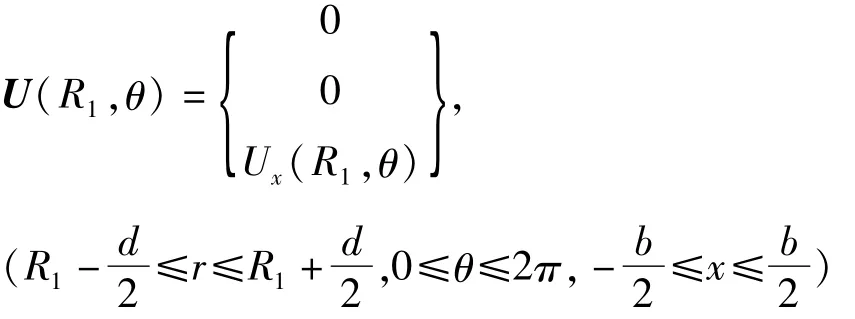
其中b，d分别为叶冠高度和宽度.经计算，公式（11）的叶冠位移场分量形式可表示为

根据表达式（12），由极坐标下的应变-位移公式［13］可算得叶冠应变

叶冠是各向同性体，由公式（13）可算得叶冠的应变能密度

其中，μ和E分别为各向同性叶冠的泊松比和杨氏模量.对（14）积分可得n节径振动的叶冠弹性应变能

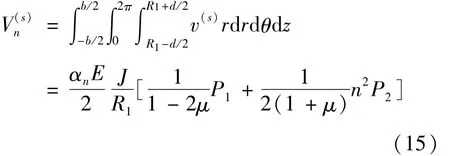
而叶冠相应的动能表达式为

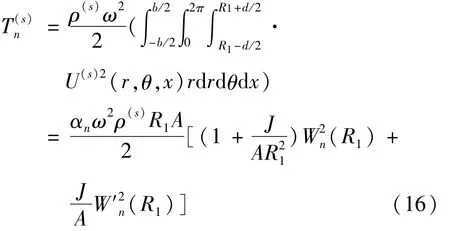
其中

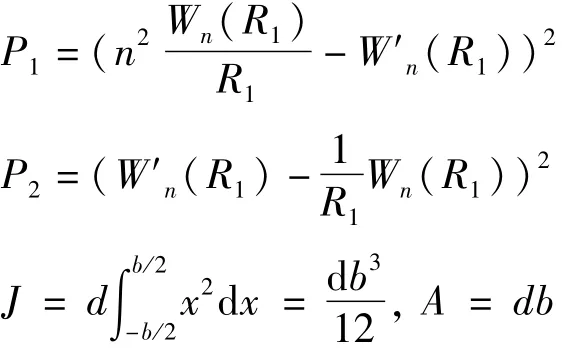
2.3 环板参数估算公式

n节径振动的带冠环板总动能和总势能分别为

用Rayleigh法可得带冠环板固有频率与弹性常数的关系式

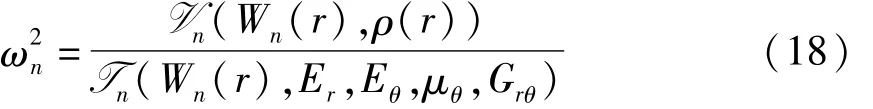
对于初始带冠叶片组，用有限元方法计算可以得到其固有频率ωn和固有模态.离散的模态向量通过函数逼近后可作为等效环板的模态函数Wn（r）.选取若干组频率ωn和模态Wn（r），求解（18）式就能确定环板弹性系数的初值.

3 算例

算例的初始叶盘模型如图1，其中叶片组的几何与材料等物理参数值见表1，均采用国际单位制.

表1 叶片组模型物理参数表Table 1 Parameter values of blade group

将表1中数据代入公式（1）～（5），计算可得环板厚度＾h＝0.0052m，密度分布函数

叶冠为各向同性的轴对称柱壳，几何与材料等物理参数值见表2，模型不需等效.

表2 叶冠模型参数表Table 2 Parameter values of shroud

叶片组的等效环板为正交各向异性材料，含有4个独立的弹性常数Er，Eθ，Grθ，μθ.考虑叶片之间相互独立，周向无相互作用，故可取泊松比μθ＝0.数值计算表明，环板径向与周向的模量比值Er/Eθ对模态计算结果影响不明显，可取Er≈Eθ.对于剩下的两个弹性常数Er和Grθ，只需用两组固有频率和模态数据、根据方程（18）确定其初值.

从文献［9］可知，在回转周期结构中，节径数大于或者等于2的振动模态不会与刚体运动发生耦合，在转子动力学分析时无需考虑.对于转子系统，工程中通常只关心前几阶临界转速［14］，只有少数较低阶的叶盘弹性模态才会与之耦合.因此，算例仅选取叶盘组合体0节径和1节径的基频和对应模态.

对带冠叶片组在内缘固定条件下作模态分析，得到0节径和1节径的基频频率分别为ω0＝586.98Hz，ω1＝1278.8Hz.

图4 带冠叶片的模态简化示意图Fig.4 Simplified modal of blade with shroud

从带冠叶片组0节径和1节径的固有模态计算结果中提取出外缘中心点的横向位移和绕周向的转角，分别作为等效环板固有模态在外缘的函数值W0（R1），W1（R1）及其导数值W′0（R1），W′1（R1）.环板的内缘为夹支边界条件，模态函数值和导数值均取为W0（R0）＝W1（R0）＝W′0（R0）＝W′1（R0）＝0.根据上述端点条件，用两点三次Hermite插值［15］就可得到0节径和1节径模态函数

将方程（20）代入方程（18），建立方程组

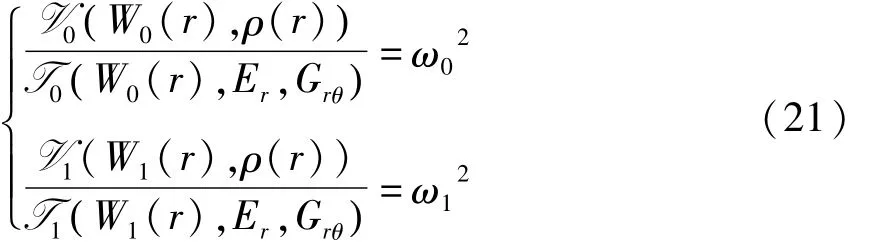
求解后得到弹性参数初值

参照式（6），设置设计变量的可行域，建立数学规划模型

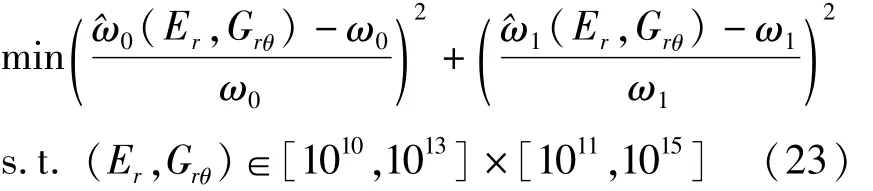
将式（22）中的数据作为初值，用NASTRAN求解序列SOL200的优化功能［16］，计算后确定环板弹性常数的终值为

将等效环板模型与初始轮盘组合即可得到缩聚叶盘模型.

图5 模型等效前后1节径模态变形云图Fig.5 Deformation fringe for initialmodel and equivalentmodel

由叶片-叶冠和轮盘构成的叶盘三维模型为回转周期结构，模态分析只需用到单个扇区的模型，节点数约为3100.由等效环板和轮盘构成的叶盘缩聚模型为轴对称结构，只需用到子午面的模型，节点数不足300.两种模型计算得到的固有频率结果如表3，其中0节径和1节径的固有频率相差分别为-4.22%和5.54%.用两种模型计算得到的1节径模态云图如图5，可以看出模态的横向等位移线基本一致.

表3 初始与缩聚模型固有频率数据结果Table 3 The natural frequencies of initial and reduced model

4 结语

介绍了用变参数环板等效大规模叶片组三维有限元模型，实现回转周期叶盘的弹性耦合振动分析的方法.分析表明，缩聚叶盘模型的自由度数可被大幅度减少，而且用缩聚模型计算得到的低阶振动固有频率具有足够精度.对于设计状态已确定的单级叶盘，等效环板和轮盘构成的组合体具有轴对称特点，计算效率高，可直接应用于转子的整体动力学计算.为转子系统的优化设计的应用提供了精度和效率兼顾的弹性叶盘缩聚模型.

1 张文.转子动力学理论基础.北京：科学出版社，1990：1～7（ZhangW.Rotor Dynamics.Beijing：China Science Publishing and Media Ltd，1990：1～7（in Chinese））

2 张欢，陈予恕.航空发动机转子系统的动态响应计算.动力学与控制学报，2014，12（1）：36～43（Zhang H，Chen Y S.Dynamic response calculation of a aero-engine′s dual-rotor system.Journal of Dynamicsand Control，2014，12（1）：36～43（in Chinese））

3 张文.转子动力学中的若干近代力学问题.中国科学基金，1994，（3）：227～229（Zhang W.Some problems of modernmechanics in rotor dynamics.Science Foundation in China，1994（3）：227～229（in Chinese））

4 Ewins D J.Vibration characteristics of bladed disks.ARCHIVE Journal of Mechanical Engineering Science，1973，15（3）：165～186

5 Kielb R E，Kaza K R V.Effects of structural coupling on mistuned cascade flutter and response.Journalof Engineering for Gas Turbines and Power，1984，106（1）：17～24

6 Genta G.On the stability of rotating blade arrays.Journal of Sound and Vibration，2004，273（4-5）：805～836

7 Omprakash V，RamamurtiV.Natural frequencies of bladed disks by a combined cyclic symmetry and Rayleigh-Ritz method.Journal of Sound and Vibration，1988，125（2）：357～366

8 王文亮，张锦，陈向钧.盘-叶耦合系统的固有模态分析-C_N群上对称结构的模态综合.固体力学学报，1988，（1）：15～23（Wang W L，Zhang J，Chen X J.Modal analysis of coupled vibration of blade and disk-modal synthesis of symmetric structures in C_N group theory.Journal of Solid Mechanics，1988，（1）：15～23（in Chinese））

9 张文，陈运西.叶片-盘-轴整体转子振动特性分析.航空动力学报，1994，（2）：120～124（Zhang W，Chen Y X. The vibration analysis of blade，disk and shaft of the whole rotor.Journal of Aerospace Power，1994，（2）：120～124（in Chinese））

10白斌，白广忱，费成巍等.改进的混合界面子结构模态综合法在失谐叶盘结构模态分析中的应用.工程力学，2015，（4）：178～184（Bai B，Bai G CH，Xue K，et.al. Application of improved hybrid interface substructure CMS method in the model analysis ofmistuned bladed disk assemblies.Engineering Mechanics，2015，（4）：178～184（in Chinese））

11杨耀乾.平板理论.北京：中国铁道出版社，1980：1～3（Yang Y K.Plate theory.Beijing：China Railway Publishing House，1980：1～3（in Chinese））

12李秋红，刘广明，薛开等.圆柱型正交各向异性圆板的自由振动分析.哈尔滨工程大学学报，2015，36（7）：981～986（Li Q H，Liu G M，Xue K，et al.Free vibration analysis of cylindrical orthotropic circular plate.Journal of Harbin Engineering University，2015，36（7）：981～986（in Chinese））

13列赫尼茨基.各向异性板.北京：科学出版社，1955：5～6（ЛехницкийСГ.Anisotropic plate.Beijing：China Science Publishing and Media Ltd，1955：5～6（in Chinese））

14郑凌云.机械振动中临界转速的工程意义及实践应用.机械研究与应用，2004，17（2）：19～20（Zheng L Y. Engineering significance and practical application of critical speed in mechanical vibration.Mechanical Research and Application，2004，17（2）：19～20（in Chinese））

15丁丽娟.数值计算方法.北京：北京理工大学出版社，2005：118～120（Ding L J.Numerical calculation method.Beijing：Beijing Institute of Technology Press，2005：118～120（in Chinese））

16隋允康.MSC.Nastran有限元动力分析与优化设计实用教程.北京：科学出版社，2004：238～257（Chen Y K.A practical course of finite element dynamic analysis and optimization design.Beijing：China Science Publishing and Media Ltd.，2004：238～257（in Chinese））

A COUPLED VIBRATION ANALYSISMETHOD OF BLADED DISK MODELBASED ON EQUIVALENT BLADE GROUP OF ANNULAR PLATEW ITH VARIABLE PARAMETERS*

Jiang Meng Zhang Meiyan Tang Guoan†
（Department of Aeronautics and Astronautics，Fudan University，Shanghai 200433，China）

Rotor systems aremostly applied in rotarymechanical devices，which play important roles in aviation，electric power，mechanical and many other industries.These systems usually consist of shaftswith multistage impellers，but a series of issues related to strength，fatigue，vibration and noise are needed to be solved.It is in an urgent to improve the performance of such products by optimization method.In rotor system，each impeller contains a blade group that composed of dozens of blades，so the DOF of the entire rotor system is still large，although the rotation period characteristics of bladed disk is used in finite elementmethod.Therefore，the calculating efficiency is still needed to be improved.For this purpose，the single bladed disk can be regarded as a designed subsystem according to aerodynamic performance requirements，and the simplification of the finite element model for the blade group is an effectiveway to improve the computational efficiency of coupled vibration of bladed disk under the premise of obtaining enough precision.In this paper，an equivalent analysismethod is put forward to simplify the blade group into an annular platewith variable parameters based on the criterion that dynamic characteristics can be approximately the same.Physical parameters of annular plate including geometric and material parameters are obtained by theoretical derivation and calculation.Eventually，the equivalentmethod is verified by taking a bladed disk model of aero engine as an example.It shows thatmodel reduction can ensure the precision with improving computational efficiency.Therefore，the equivalent analysismethod is an efficientmodeling approach of bladed disk for the future optimization of the whole rotor systems.

vibration， blade， disk， rotor， model reduction

10.6052/1672-6553-2016-046

2016-04-11收到第1稿，2016-05-26收到修改稿.

*国家自然科学基金项目资助项目（11572089）

†通讯作者E-mail：tangguoan＠fudan.edu.cn

Received 11 April 2016，revised 26 May 2016.

*The project supported by the National Natural Science Foundation of China（11572089）

†Corresponding author E-mail：tangguoan＠fudan.edu.cn