Will Informed Traders Share Information with Each Other?*
LING Peng
(China Economics and Management Academy, Central University of Finance and Economics, Beijing 100081, China)
Abstract This paper introduced two heterogeneous insiders into Kyle model, and based on theoretical deduction, explored the possibility that they shared information with each other. The paper finds that in equilibrium, the expected profit of the insider is a decreasing function with respect to the number of information to share. When the two insiders do not share any information, their expected profits can reach the maximum. The conclusion is that insiders have no incentive to share any information.
Key words Kyle model, heterogeneous insiders, information sharing, expected profit
1 Introduction
Kyle (1985)[1]defined a competitive equilibrium with one insider (the informed trader), one noise trader, and one market maker in his groundbreaking article. In this paper, he pointed out that insider trader could benefit from having private information on risky assets. Subsequently, many scholars extended Kyle's model. Some scholars introduced public information or shared information into Kyle model (Luo, 2001; Liu and Zhang, 2011)[2-3], having a conclusion that public information or shared information could damage the profits of insider traders and make prices contain more information; Admat and Pfleiderer (1988)[4]extended the number of insider trader in Kyle model toN, and assumed they could observe the same information. They found that the total expected profits of all insider traders gradually went to zero asNincreased, and the information contained in price also increases as the competition increases. Holden and Subrahmanyam (1992)[5]also introducedNhomogeneous informed traders and generalized the one-shot trading model by examining a model in which a number of auctions take place sequentially. They found that insiders would compete fiercely on private information and lead to more information leakage. Besides, when there are more insider traders or more auctions, the competition becomes more intense.
Since the assumption that insiders are homogenous is too harsh, Foster and Viswanathan (1993)[6]firstly introduced heterogeneous informed traders into Kyle model, exploring the impacts of information correlation on the equilibrium. They found that the profits to the informed traders are lowest with identical information since there is a strong competition between traders. And the profits are the highest and higher than the case where the correlation coefficient is zero when the correlation is positive but not too high. Thus they get a conclusion that when traders have heterogeneous private information, the competitive pressure between them can be effectively mitigated. based on Foster and Viswanathan (1996)[7], Back and Cao (2010)[8]further investigated the continuous case. Dridi and Germain (2009)[9]studied the one-period trading model, assuming insiders are heterogeneous. Then they found that noise to some extent could ease the competition among insiders, especially when there are many of them (N≥4). The existence of moderate noise can maximize the trader's profits. Boco and Germain (2016)[10]also came to similar conclusions. Besides, they also explored the situation of many trading periods. Through numerical simulation, they found that when the competition intensity between insiders is very high (that means the number of traders or trading periods is high), noise to a certain extent could improve insider’s expected profits by alleviating the competition among them.
Vives(1984)[11]studied a duopoly model where firms have private information about an linear demand. And he discussed the situation where the monopoly companies would share its private information with each other. Inspired by him, in this article we want to explore whether insiders will share information or under what circumstances they will share information, when there are two heterogeneous insiders. As we all know, on the one hand, information sharing can increase the precision of information for each informed trader. This is the positive effect. But it also can increase the competition among the insiders, causing certain negative effects. For the question that whether insiders are motivated to share information, there is still a lack of relevant research here. In view of this, we will explore this issue in the article. In the second section, we explore whether they will share information when each insider receives only one observation. In the third section, we discuss the situation of each insider receiving multiple observations and discuss whether there is an optimal amount of information sharing level between them. The fourth section is our conclusion.
2 The model
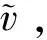
1) Profit maximization: informed traders choose the optimal asset demandxito maximize their expected profits based on the private information they observe.xisatisfies
(1)
2) Market efficiency:

(2)
In order to obtain the equilibrium for the model, we need the following lemma as preparatory conditions.
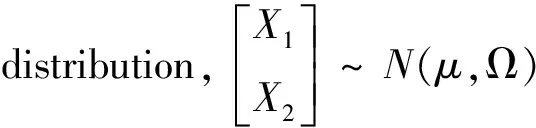
(3)
According to Lemma 1, we can calculate
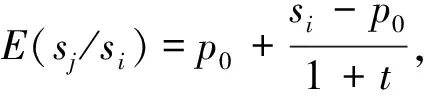
(4)
(5)
Theorem1When the insiders do not share information, there is a unique linear equilibrium that satisfies the definition of equilibrium. That is
(6)
(7)
The proof of this theorem is postponed to the Appendix
Based on the equilibrium, we can calculate the expected profit of each insider when the insiders do not share information.
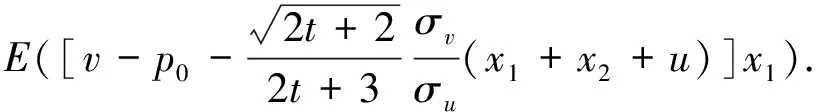
(8)
Substitute eq.(6) into eq.(8) and rearrange, we can get

(9)
When insiders decide to share information by making a contractual arrangement, the information sets obtained by the two insiders are actually the same. For each insider,s1ands2can all be observed. Information sharing increases the precision of the signal obtained by each insider and at the same time increases the correlation of signals. At this point, the model actually becomes a situation with two homogeneous insiders. we give the equilibrium as below.
Theorem2When the two insiders share information, the linear equilibrium of the model is
(i=1,2),
(10)

(11)
The proof of this theorem is postponed to the Appendix
Similarly, we can calculate the expected profit of each insider when the two insiders share information.
(12)
Substitute eq.(10) into eq.(12) and rearrange, we can get
(13)
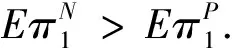
Theorem3When there are two heterogeneous insiders, not sharing information can bring more profits to insiders. That is to say, insiders will not choose to share information with each other.
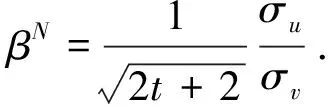
Therefore, we can see that information sharing can cause two effects. On the one hand, it can increase the amount of observation that each internal trader receives about the risky asset, increasing the precision of information. This is the positive aspect. On the other hand, information sharing increases insider's competition for information and makes insiders to trade more aggressively, which leads to more information leakage. This is the negative aspect. From Theorem 3, we can see that the negative aspect dominates.
3 The case of multiple observations
In the previous section, we assumed that each insider can only receive one observation. Thus the insiders face the choice of either not sharing information or performing complete information sharing. There is no transitional situation. So if we assume that insiders can receive multiple independent observations and they can choose to share part of them, what would the result be? What is the optimal number of observation to share? We will discuss this issue in this section.

(14)
We useP1andSto denote the private information and shared information insider 1 has. Then the conditional expected profit of insider 1 is
E((v-p)x1/P1,S)=
E[v-η-λ(x1+x2+u)/P1,S].
(15)
By the first order condition, we have
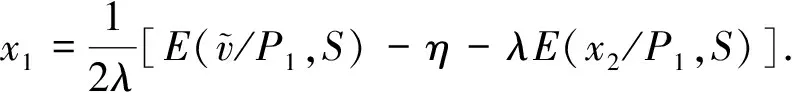
(16)
According to lemma 1, we have
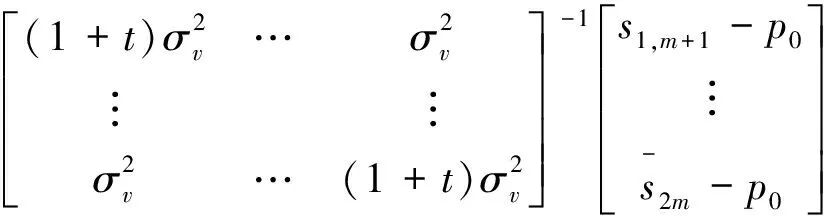
(17)
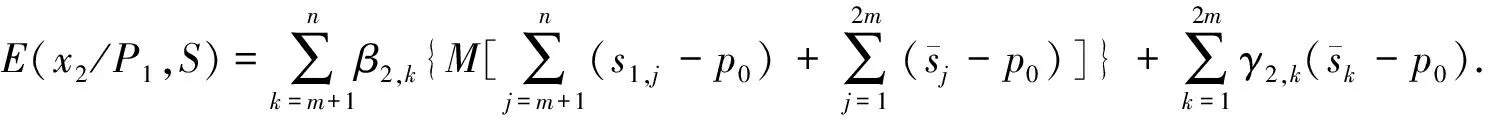
(18)
Substitute eq.(17) and eq.(18) into eq. (16) and Compare the coefficients, and we can get
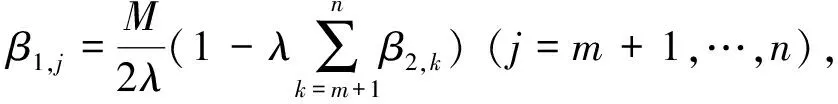
(19)
(j=m+1,…,n).
(20)
By the first order condition of insider 2, we can get similar result. And from the equation it can be easily found that if there exist a linear equilibrium, we must have
β1,m+1=…=β1,n=β2,m+1=…=β2,n,
(21)
γ1,1=…=γ1,2m=γ2,1=…=γ2,2m.
(22)
Thenxican be expressed as
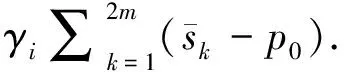
(23)
Let

(24)

(25)
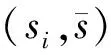
Theorem4When each insider choose to sharemobservations, the linear equilibrium of the model is
(i=1,2),
(26)
(27)
The proof of this theorem is postponed to the Appendix.
Then the expected profit of each insider is
Eπ1=Eπ2=E((v-p)x1)=
u)]x1).
(28)
Substitute eq.(26) into eq.(28) and rearrange, we can get
(29)
Letn=1,m=0 orn=1,m=1, and we can get the situation as section 2 shows.
For the insiders, they will choose an optimal contract, which is an optimalm, so as to maximize their own expected profits. From the expression of expected profit, we cannot intuitively see whether the expected profit is an increasing or decreasing function ofm. We can only use the derivative method. Take the logarithm of the above equation, and we can get
(30)
Take the partial derivative of this equation with respect tom, and we have
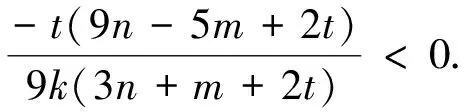
(31)
From eq.(31) we can see thatEπ1is a decreasing function with respect tom. So we have
Theorem5In equilibrium, as the insider increases the number of observation to share, his expected profit decreases. So when the insider does not share any information, i.e.m=0, the expected profit reaches a maximum value.
Now we can answer the questions raised earlier. When insiders can receive multiple observations, the optimal strategy is still not to share any information. That is to say they have no incentive to make a contract to share information. This is because information sharing increases the correlation between signals received by insiders, increasing the competition. Thus insiders will trade more aggressively, leading to more information leakage. Although information sharing will improve trader's information accuracy, the negative effect it brings still dominates the positive effect.
Now we consider the effectsnandthave on the expected profit. Take partial derivative with respect tonandtrespectively, and we have
(32)
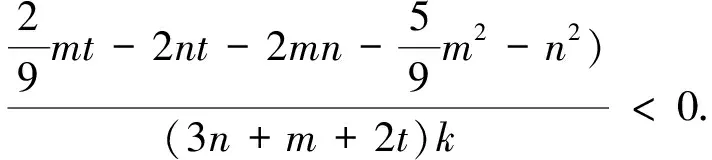
(33)
Theorem6Keepingtandmconstant, the expected profit of each insider increases withn. While keepingnandmconstant, the expected profit of each insider increases with the precision of the observation.
The economic meaning is simple. Whennis bigger, each insider has more pieces of information. And the precision of his overall information increases, bring more expected profit. Similarly, whentis smaller, the information obtained by the insider is higher, leading to higher expected profit.
4 Conclusion
When assuming insiders can receive heterogeneous information, will they have incentive to share information with each other? Through research, we find that the answer is no. although information sharing can improve the precision of the information each insider obtains, it can also increase the competition between insiders, causing some negative effects. And the negative effect of information sharing dominates.
5 Appendix A. Proofs
ProofofTheorem1suppose that the linear equilibrium of the model is
xi=αi+βi(si-p0),p=η+λy.
(A.1)
The optimization problem of insider 1 is
E((v-p)x1/s1)=E([v-η-λ(x1+α2+
(A.2)
By the first condition, we have
(A.3)
Similarly, we have
(A.4)
Compare coefficients and apply symmetryα1=α2,β1=β2, we have
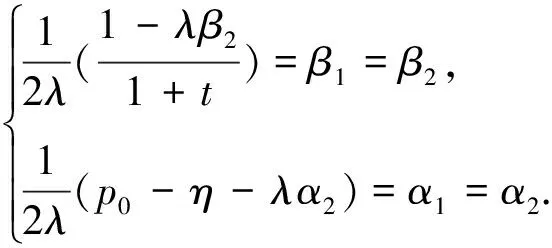
(A.5)
The solution is
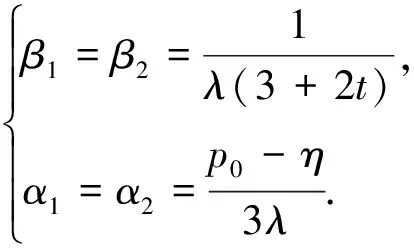
(A.6)
According to the pricing mechanism of the market maker, we have
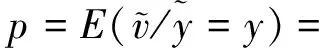
(A.7)
(A.8)
Compare coefficients and we can get
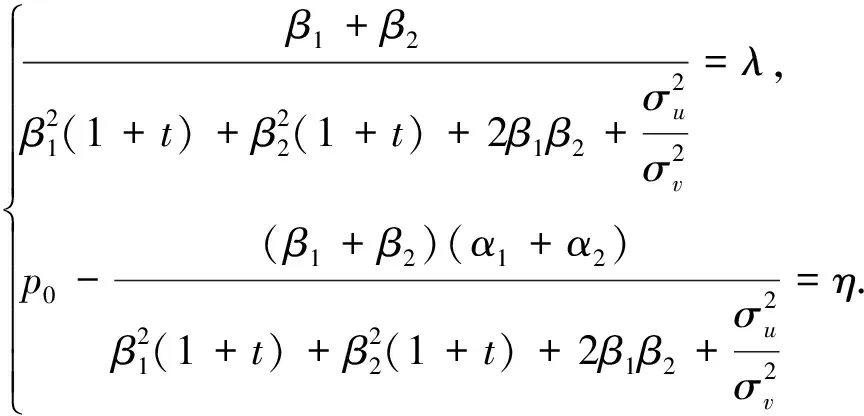
(A.9)
According to (A.6) and (A.9), we have
α1=α2=0,η=p0,
(A.10)
(A.11)
ProofofTheorem2suppose that the linear equilibrium of the model is
xi=αi+βi(s1-p0)+γi(s2-p0),p=η+λy.
(A.12)
The optimization problem of insider 1 is
E((v-p)x1/s1,s2)=
E([v-η-λ(x1+x2)]x1/s1,s2).
(A.13)
By the first condition, we have
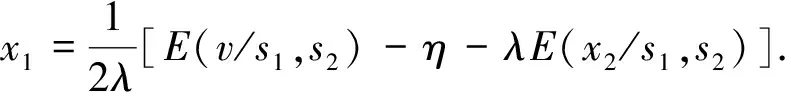
(A.14)
According to lemma 1, we have
(A.15)
E(x2/s1,s2)=α2+β2(s1-p0)+γ2(s2-p0).
(A.16)
Substitute eq.(A.15) and eq.(A.16) into eq.(A.14), we have
(A.17)
Similarly we can get the equation ofx2. Compare coefficients and apply symmetryα1=α2,β1=β2, we have
(A.18)
The solution is
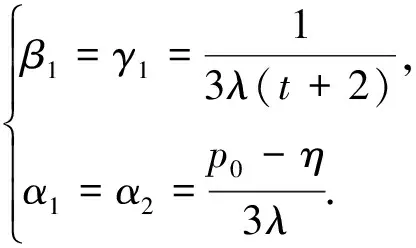
(A.19)
According to the pricing mechanism of the market maker, we have
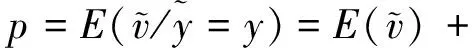
(A.20)
Substitute and rearrange, we have

(A.21)
Compare coefficients and we can get

(A.22)
According to eq.(A.6) and eq.(A.9), we have
α1=α2=0,η=p0
(A.23)
(A.24)
Proof of Theorem 4: suppose that the linear equilibrium of the model is
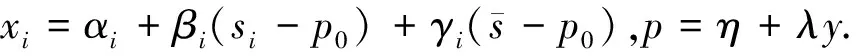
(A.25)
The optimization problem of insider 1 is
(A.26)
According to lemma 1, we have
(A.27)
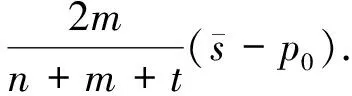
(A.28)
Substitute eq. (A.27) and eq.(A.28) into eq.(A.26) and take the first-order condition, we can get

(A.29)
Similarly we can get the equation ofx2. By comparing coefficients and apply symmetryα1=α2,β1=β2, we have

(A.30)
The solution is
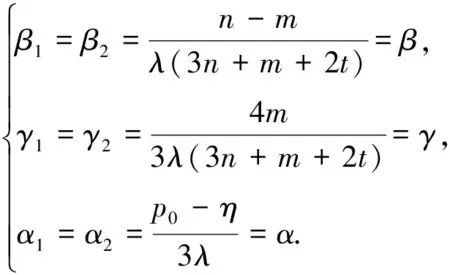
(A.31)
According to the pricing mechanism of the market maker, we have

(A.32)
Combine eq.(A.16) and eq.(A.17), we can get
α1=α2=0,η=p0
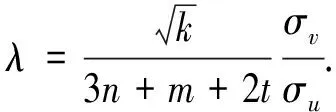
(A.33)

