基于平均模型的三相四线制逆变器多管开路故障诊断
李 战,王伯荣,马 皓,白志红
(浙江大学电气工程学院,杭州310027)
三相四线制逆变器在有源滤波、新能源并网等领域得到广泛研究和应用[1-2],提高三相四线制逆变器的可靠性有着重要意义。故障容错是一种提高变换器运行寿命的有效措施,而快速准确的故障诊断是容错运行的前提。
行业调查显示,在电力电子变换器中开关器件是最容易失效的元件之一[3]。因此,有很多故障诊断的研究是针对开关器件的。逆变器中的开关管(主要是IGBT)的故障可分为开路故障和短路故障,其中开路故障通常不会导致系统立即停机,而可能引发其他更恶劣的系统故障,近年来受到了越来越多的关注[4]。针对逆变器开关管开路故障,国内外已经提出了大量方法,其中一些基于智能算法[5-7],因计算量大而一般不用于在线快速诊断。而其他在线诊断的方法,又可以分为基于电流、基于电压和基于模型3类。
基于电流的方法,如基于电流矢量[8-9]、基于平均电流[10]、基于电流误差[11]、基于零电流[12]等,利用故障后输出电流的特征进行诊断,这些方法适用于稳定运行的逆变器,而在含有大量谐波和三相不对称的场合诊断时间长,而且可能产生误判。
基于电压的方法则通过提取电压信号的故障特征进行诊断。文献[13]直接将输出电压和其参考值进行比较而进行诊断;为了提高诊断速度,基于桥臂中点电压和驱动逻辑[14-15]、基于桥臂间电压和驱动逻辑[16-17],以及基于门电压特征[18-19]的方法被提出。这些方法最快能在1个开关周期内完成诊断,且对逆变器运行状态依赖小,但需要额外的硬件电路和大量的调试,这增加了成本和设计难度。
为了不增加硬件电路又能实现快速诊断,一些基于模型的方法被提出。文献[20]构建了一个模型参考自适应系统去观测输出电压畸变来进行诊断;文献[21-22]则分别使用Luenberger观测器和混合逻辑动态模型去观测输出电流畸变进行诊断。这些方法是针对三相三线制逆变器的,且不能进行任意多管的诊断。对于三相四线制逆变器,文献[23-24]分别提出了针对两电平和三电平逆变器多管诊断方法,都是基于逆变器交流侧输出电压矢量和占空比的对应关系,并取得了不错效果。但这些方法对于死区、延时、采样误差、电感误差等影响的处理不是通过模型本身的优化,而是通过延长最短诊断时间,诊断速度和鲁棒性依然有待优化。
针对以上方法的问题,本文提出了一种新的基于平均模型的方法,可以实现对三相四线制逆变器任意多管的快速诊断。该方法将平均实际桥臂中点ARP(average real bridge-arm pole)电压与平均期望桥臂中点 AEP(average expected bridge-arm pole)电压的偏差作为诊断特征量,诊断阈值自适应于死区、延时、采样误差、电感偏差等因素的影响,保证了高鲁棒性和诊断速度;只需要系统控制器已经使用的信号,无需额外的硬件和采样,计算量小,实现方便。
1 逆变器开关管开路故障分析
图1是三相四线制逆变器拓扑。为了分析简便,假定桥臂上下管驱动完全互补。定义每相的驱动信号为 SX(X=A,B,C),上管 TAU开通时,SX为 1;下管TAL开通时SX为0。当逆变器正常时,桥臂中点电压完全跟随驱动信号,把正常状态下的桥臂中点电压定义为期望桥臂中点电压,表示为

式中,Vdc为直流侧电压。当开关管开路故障发生时,则式(1)不成立。
以X相上管TXU开路故障为例进行分析。当TXU发生故障时,另外两相的桥臂中点电压的实际值仍然与期望值一致。根据相电流 ix(x=a,b,c) VXL分以下 3种情况讨论,如图2所示。
(1)ix为正:此时 VXL为 0,有。
(2)ix为负:此时系统不受故障影响,即。
(3)ix为 0:当 SX为 0 时,定有 VXL为 0;而当SX为1时,此时X点电势和x电势相等,其值受输出电压和另两相运行状态的影响,但易分析得到VXL必定低于Vdc,否则ix不再为0。所以,有。
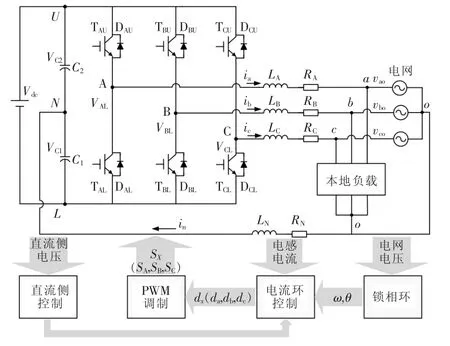
图1 三相四线制逆变器Fig.1 Three-phase four-wire inverter

图2 TXU发生故障时的3种情况Fig.2 Three circumstances when fault occurs to TXU
综上所述,当TXU发生开路故障时,存在VXL≤。定义桥臂中点电压偏差为

分析得到桥臂中点电压偏差故障特征,如表1所示。
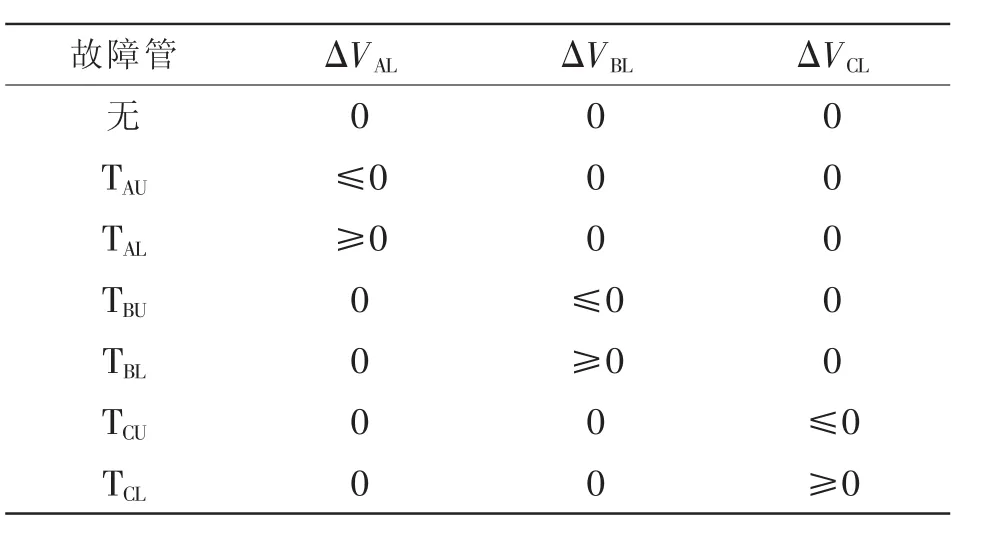
表1 不同开关管故障时桥臂中点电压偏差特征Tab.1 Characteristics of bridge-arm pole voltage deviations for different faults
2 基于平均模型的诊断方法
2.1 基本原理
由上述分析可知,不同开关管开路故障时,桥臂中点电压偏差呈现不同特征,因此可以用来进行故障诊断。如果对桥臂中点电压进行实时采集,则需要增加额外的硬件电路或者很高采样频率,这增加了软硬件负担。而桥臂中点电压的开关平均却可以通过已有的电压电流等信号进行计算。本文提出将平均桥臂中点电压的偏差作为诊断变量,推导了相应的计算模型。

基于平均模型诊断方法的原理如图3所示。AEP电压通过输入电压、占空比进行计算。ARP电压由输出电压、电流、直流侧中点电压和电感等进行计算。
式中:TS为开关/采样周期;t[n]为第n个采样时刻。
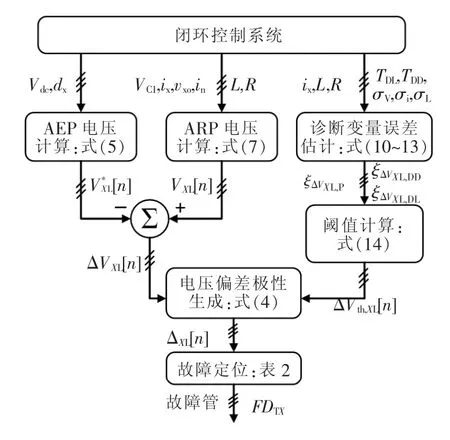
图3 基于平均模型诊断方法的原理Fig.3 Principle of the average model-based diagnosis method
理想情况下,当无故障发生时,ΔVXL[n]应该为0。但死区、延时、采样误差、电感偏差等会造成一定的计算误差,从而使得无故障时ΔVXL[n]也不为0。有必要对这些误差进行分析,并根据这些误差选择合适的故障检测阈值,由此应用了一种自适应于误差的灵活阈值方法。如图3所示,阈值会在计算诊断变量的同时进行计算更新。根据确定好的阈值,得到偏差极性ΔXL[n]为
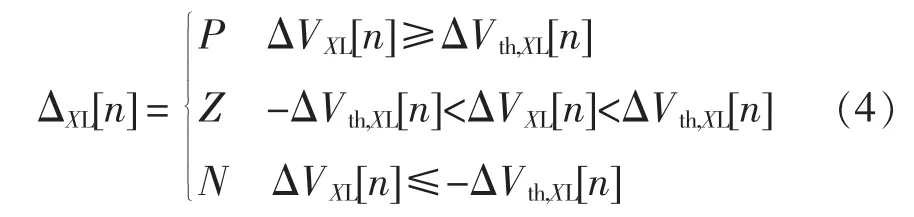
为了进一步提高鲁棒性、抵抗噪声等干扰的影响,引入了最少次数Kmin来确定偏差极性。比如Kmin=2时,ΔVXL[n]要保持至少2个周期为P/N,才被判定为P/N,否则为Z。一般来说,Kmin设为2就足够应付瞬时干扰,当然在某些应用情况下为了保证鲁棒性,可以将其设置更高。在本文中,Kmin设为2。
每一相桥臂中点电压特征只跟本相开关管故障相关。再根据表1,可以得到单管及任意多管故障诊断规则,如表2所示。
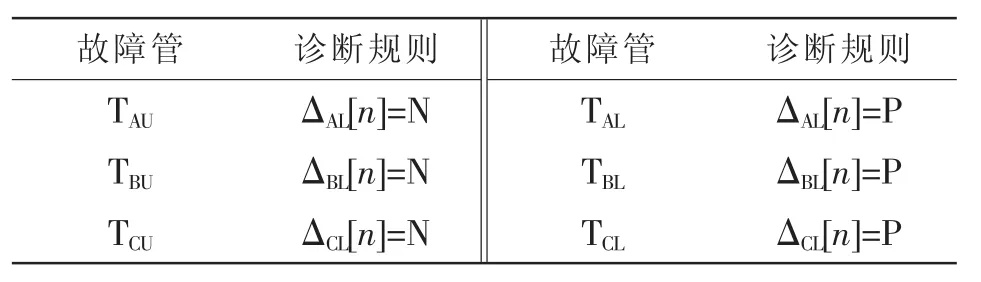
表2 故障诊断规则Tab.2 Fault diagnosis criteria
2.2 平均桥臂中点电压计算模型
图4展示了2种常见DSP PWM调制和桥臂中点电压期望值的波形。在两种模式下,可以得到相同的计算公式为
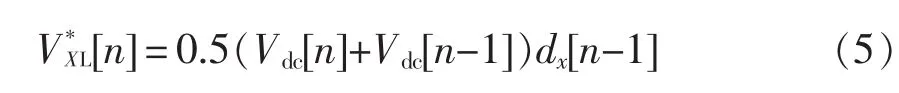
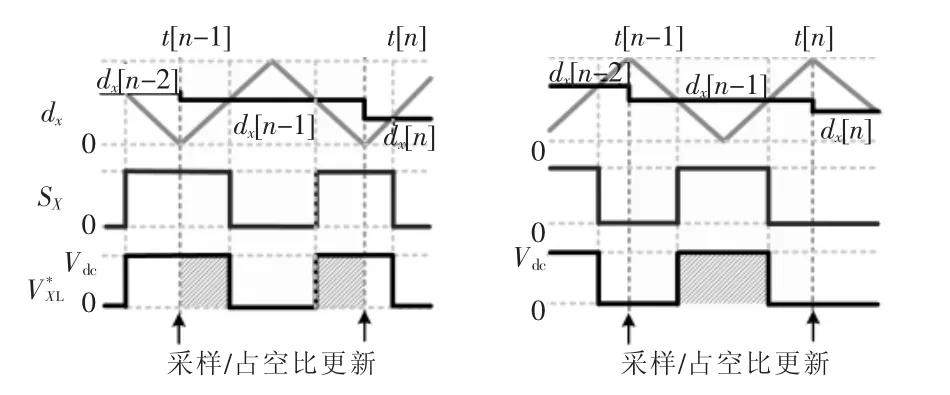
图42 种基于DSP的PWM调制波形Fig.4 Two DSP-based PWM modulation waveforms
值得注意的是,在某些情况下,当过调制时,占空比可能超过1,此时占空比应该算作1。
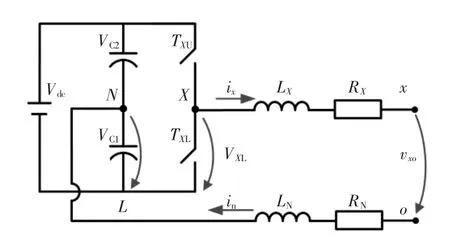
图5 计算平均实际桥臂中点电压的简化电路Fig.5 Simplified circuit for calculating ARP voltage
根据图5和式(3),可以得到
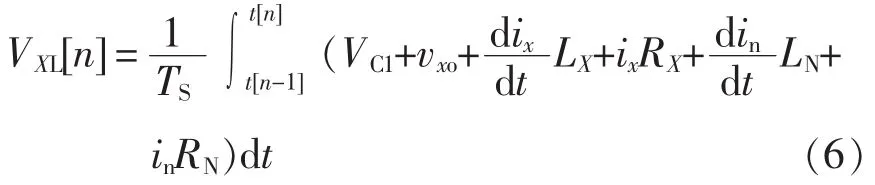
经过简化,可以得到VXL[n]的离散形式为
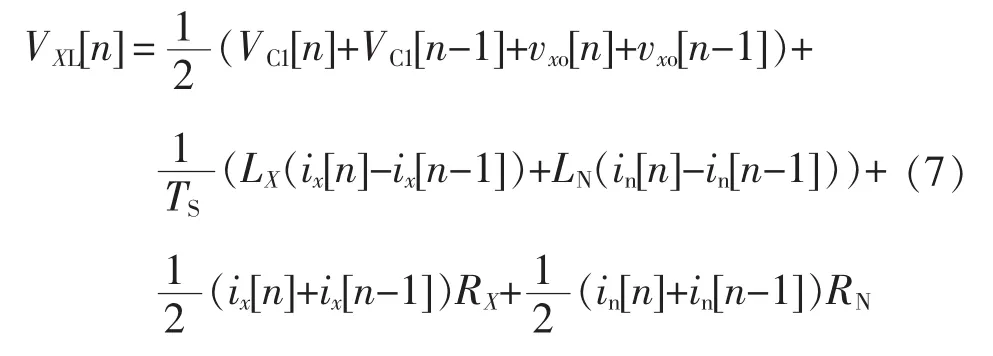
其中,in[n]=ia[n]+ib[n]+ic[n]。
3 误差分析及阈值选择
3.1 采样和参数偏差导致的计算误差
设函数y为

式中,x1,x2,…,xn是采样的信号或参数等变量。
设 σx1,σx2,…,σxn是各个变量 x1,x2,…,xn本身的误差,则变量误差导致函数y的总误差ξy可以计算为

所提诊断变量ΔXL[n]计算模型中,采样的电压电流信号本身带有一定的采样误差。模型中的电感与实际电感因为生产不一致性、测量误差和老化等原因而可能有较大偏差。另外线路等效电阻和中线电感很小,对误差的影响可以忽略。
根据式(6)、式(7)和式(9),可以得到 ΔVXL[n]由变量本身误差造成的总误差为
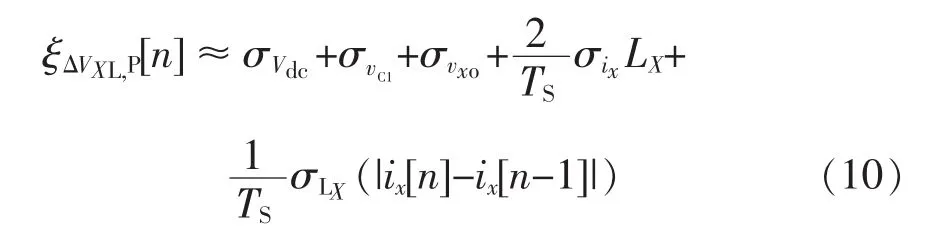
3.2 死区和延时导致的计算误差
除变量误差外,死区和延时也是带来计算误差的重要因素。死区TDD的影响如图6所示。易得到死区造成的诊断变量计算误差为
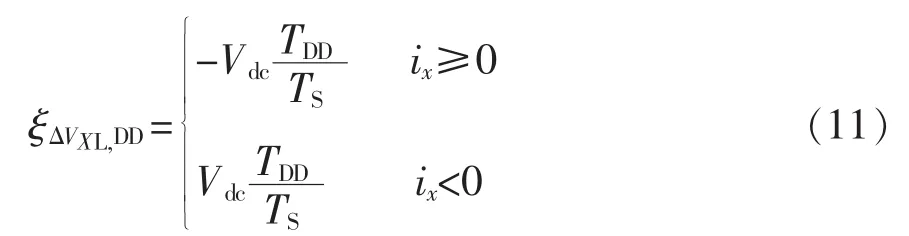
式(11)可以用来补偿死区带来的误差,但这需要对电流极性进行判断,电流过零时可能不准确。一种简单有效的处理方式就是在设定阈值时考虑死区可能造成的最大误差,即
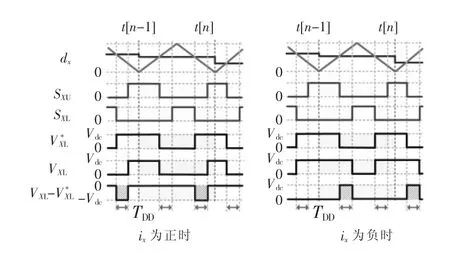
图6 死区对计算误差的影响Fig.6 Effect of dead time TDDon calculation error

类似地,可以分析延时TDL带来的最大误差,即

3.3 阈值的选择
在故障诊断中,一般都设有阈值来避免误诊断。在本文所提方法中,阈值主要用来消除诊断变量计算误差的影响,所以所设定的阈值需要涵盖由采样误差、参数偏差、死区延时等因素的影响。式(10)~式(13)中对于误差的估计已经是基于最坏情况,所以可以设定阈值为
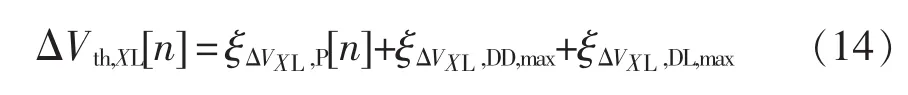
4 实验验证
实验参数如表3所示,实验结果如图7~图11所示。
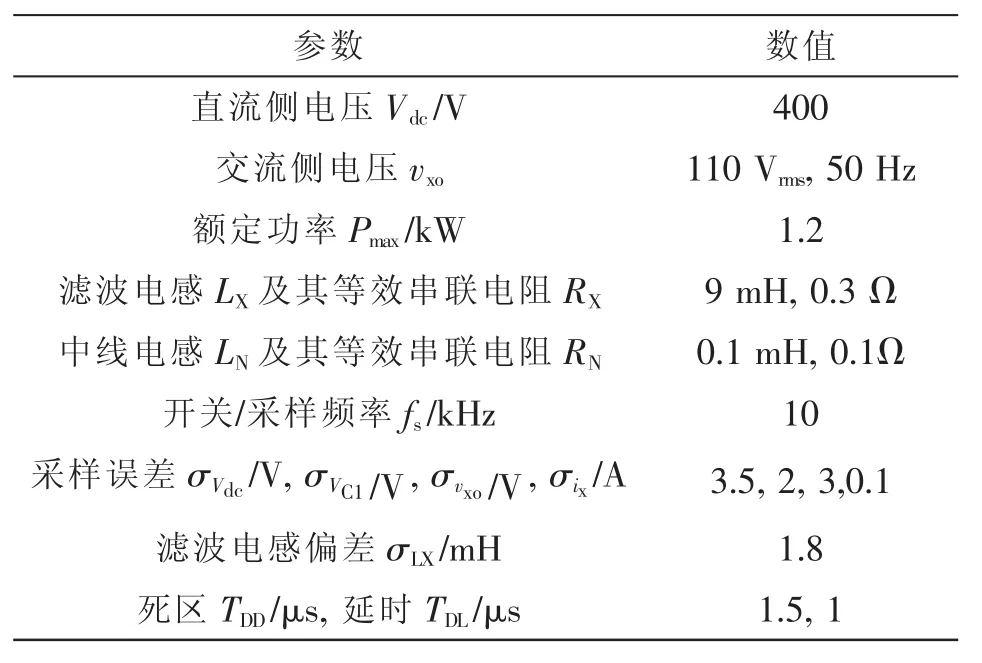
表3 实验参数Tab.3 Experimental parameters
图7给出了存在功率切换、采样误差和电感偏差等不良因素时的实验结果。采样误差和电感偏差见表3,在不良因素共同影响下,都能保证诊断变量低于阈值而避免误诊断,证明了该诊断方法对干扰的抵抗性。值得注意的是,由于电感偏差存在,诊断变量在切换瞬间有大误差,但采用误差自适应的灵活阈值,阈值也相应升高从而避免误诊断,这体现了误差自适应阈值的有效性。
图8和图9分别给出了在逆变运行状态和整流运行状态下TAU、TBU和TCL三管同时故障及诊断的实验结果。实验结果表明,不管是逆变状态还是整流状态,多管故障都能准确诊断,其最快诊断时间为0.2 ms(2个开关周期),这证明了所提诊断方法对多管诊断的有效性和快速性。

图7 逆变器无故障时功率切换下实验波形Fig.7 Experimental waveforms of inverter with power changes under normal operation
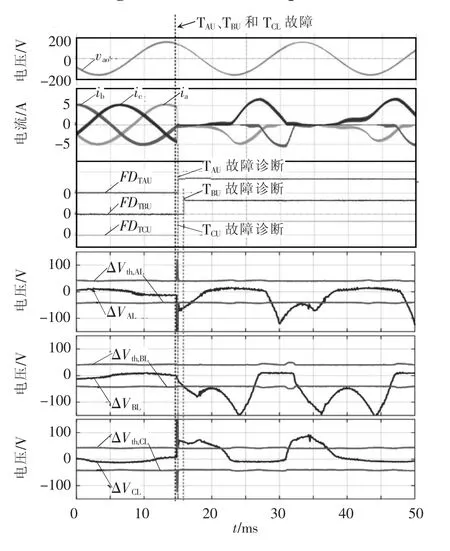
图8 逆变状态下TAU、TBU和TCL开路故障及诊断实验波形Fig.8 Experimental waveforms of TAU、TBUand TCLopencircuit faults and diagnosis in inverter mode
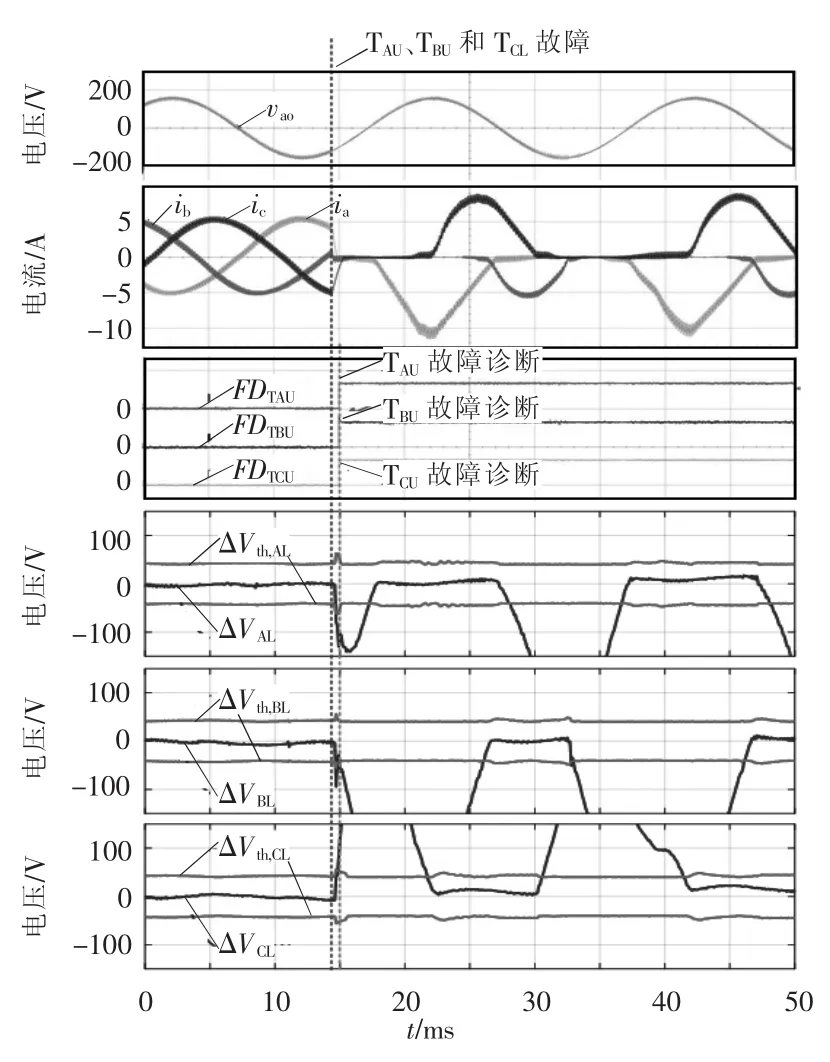
图9 整流状态下TAU、TBU和TCL开路故障及诊断实验波形Fig.9 Experimental waveforms of TAU、TBUand TCLopencircuit faults and diagnosis in rectifier mode
图10给出了诊断方法在电网不对称情况下的有效性。在该实验中,B相电网电压幅值比其他两相低20%,电网电压中除正序分量外,还存在负序分量和零序分量。实验结果表明,该诊断方法不受电网不对称的影响。

图10 电网电压不对称情况下TAU开路故障及诊断实验波形Fig.10 Experimental waveforms of TAUopen-circuit fault and diagnosis with asymmetric grid voltage
图11是空载情况下TAU开路故障及诊断实验波形,为了验证该方法对于不同负载的适用性。该实验中负载电流为0,故障发生后无法被诊断,这表明该方法的诊断效果受负载的影响。负载电流很低时,开关管开路故障不能引起足够的桥臂中点电压偏差来实现诊断,所以该方法不适用于空载和低载情况。
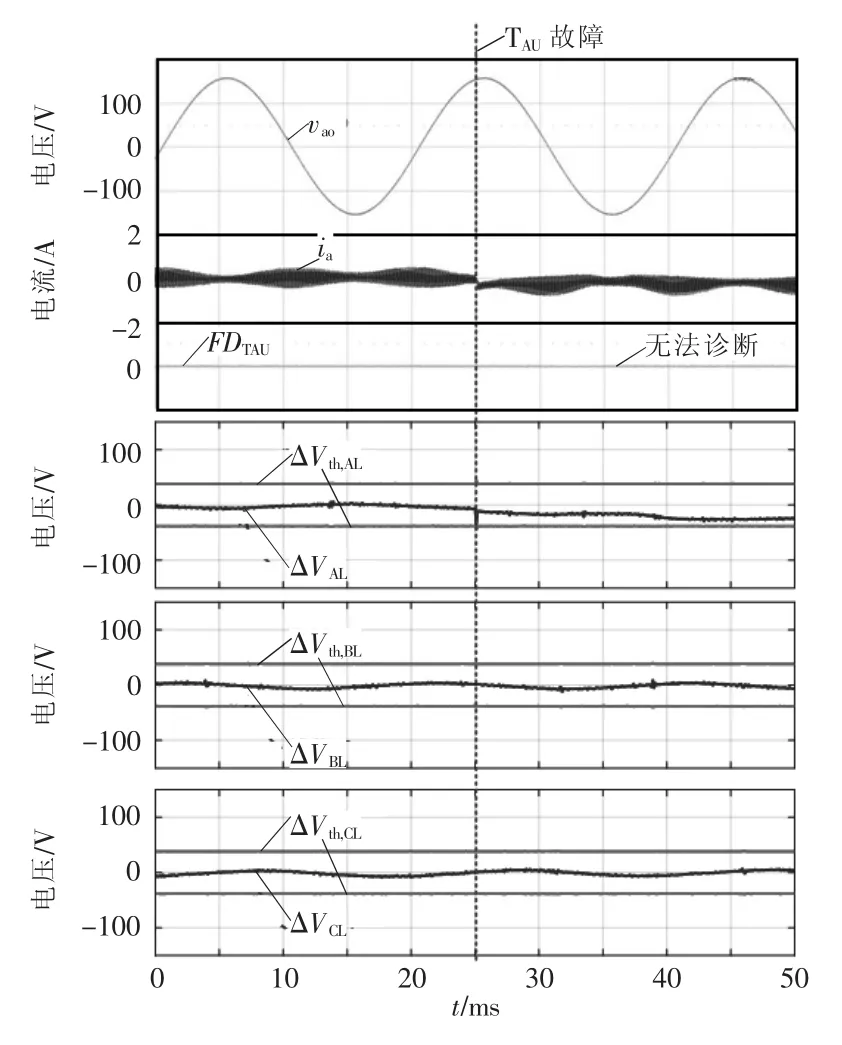
图11 空载情况下TAU开路故障及诊断实验波形Fig.11 Experimental waveforms of TAUopen-circuit fault and diagnosis without power output
5 结语
本文构建了一种针对三相四线制逆变器任意多管故障的快速可靠的诊断方法。该方法基于平均桥臂中点电压和误差自适应阈值,以ARP电压与AEP电压的偏差作为诊断变量,对故障响应快,保证了诊断的快速性,诊断时间最短为2个开关周期。此外,采用误差自适应的灵活阈值保证了高鲁棒性,可以抵抗功率突变、采样误差和电感偏差等不良因素的干扰。此方法不受电网不对称的影响,但不适用于负载电流很低的情况;计算量小,无需额外的硬件电路和信号采样,可以很方便地嵌入到控制程序中,具有实用性强的优点。最后,实验结果验证了该诊断方法的有效性。

