基于双有源桥DC/DC变换器回流功率优化的变频移相混合控制策略
任伊昵,高祎韩,韩 旭,马 皓
(浙江大学电气工程学院,杭州 310027)
双有源桥 DAB(dual active bridge)DC/DC 变换器能够实现能量双向流动和器件的零电压开关ZVS(zero-voltage switching),具有高效率、低成本、高功率密度等特点。近年来随着电动汽车、不间断电源、新能源发电等技术的发展,双有源桥变换器得到了越来越广泛的应用[1]。
电动汽车充电过程中,电池电压随电量宽范围变化,充电机需要在输出电压宽范围变化的基础上满足恒流输出,因此变换器需要实现宽范围高效能量传输。
传统的双有源桥电路通常采用单移相SPS(single-phase shift)控制方式[2-3],这种方法控 制简单,便于实现软开关,具有较高的传输效率。然而,该方法存在无功能量回流问题,在输入输出电压不匹配时,能量回流严重,并难以实现软开关,增加了变换器的损耗。为了解决SPS控制存在的问题,文献[4-6]提出了加入全桥内移相角的双重移相DPS(dual-phase shift)控制,通过分析双重移相控制的的回流功率特性,提出了优化的控制策略;文献[7]针对开关电流应力进行了控制策略优化,但这些文献都没有考虑输入输出电压在宽范围变化时变换器的工作特性;文献[8]分析了变换器宽范围工作时的软开关特性,并以最小电感电流为目标进行了控制优化,然而没有考虑回流能量对系统效率的影响;文献[9-10]分析了包括了变频控制的双有源桥电路,但只针对轻载情况进行频率调节。
为了实现宽范围能量传输,使变换器在全负载范围工作在最佳效率点,本文首先分析了DPS控制的最小回流功率工作曲线,寻找DPS控制最佳工作点,并在此基础上提出变频移相混合策略,最后通过实验验证其正确性和可行性。
1 双有源桥DC/DC变换器工作原理
1.1 单移相控制工作原理
图1为双有源全桥DC/DC变换器原理典型电路,电路包括高频变压器T、电感L、变压器两端的双有源全桥、两侧电容 C1、C2以及电源 U1、U2。
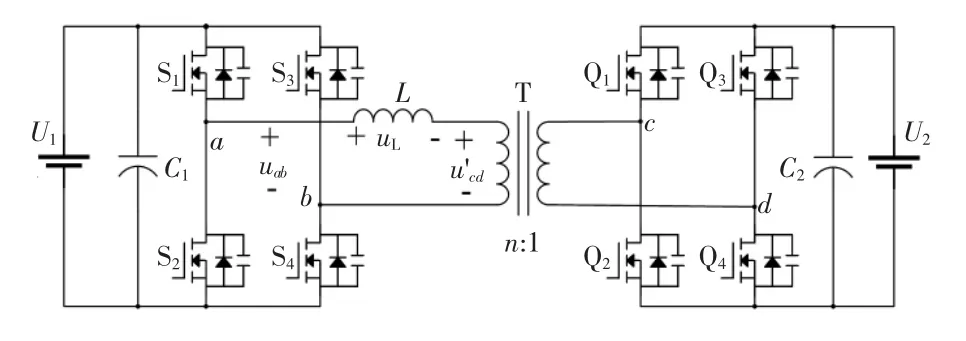
图1 双有源桥DC/DC变换器原理Fig.1 Schematic of DAB DC/DC converter
在稳态工作时,两侧全桥的上下开关管互补导通,开关频率均为fs,忽略开关过程,全桥中点电压uab、ucd可以近似认为高频交流方波。以功率正向传输为例,变压器两端电压uab、电感两端电压u'cd以及电感电流iL波形如图2所示,图中,Dφ为uab和ucd基波移相占空比,即移相角φ与π的比值。
在图2的工作状态下,开关管Q1在t1时刻电流为负,此时电感电流通过MOS体二极管续流,Q1两端电压为0,此时开通Q1能够实现零电压开通。同理,此时全部开关器件均可实现零电压开通。

图2 单移相控制典型波形Fig.2 Typical waveforms of SPS control
然而,当输入电压与输出电压不匹配时,工作波形会转变为图2中虚线状态。这种工作状态下,开关管Q1在t1时刻没有电流通过,Q1两端电压为输出电压,无法实现零电压开通。同时,由于输入、输出电压的不匹配,导致t1~t2时刻电感电流di/dt不为0,电感峰值电流增大,同时无功回流能量增大。因此,当输入电压与输出电压不匹配时,采用单移相控制方式功率传输效率较低。
1.2 双重移相控制工作原理
由于采用单移相控制方式,输入、输出电压不匹配时会造成无功电流增大、无法实现软开关等问题,因此,对电压较高的一侧全桥电路加入内部移相,降低电压有效值,能够有效减小无功回流,并能实现电压不匹配时所有开关器件零电压开通。
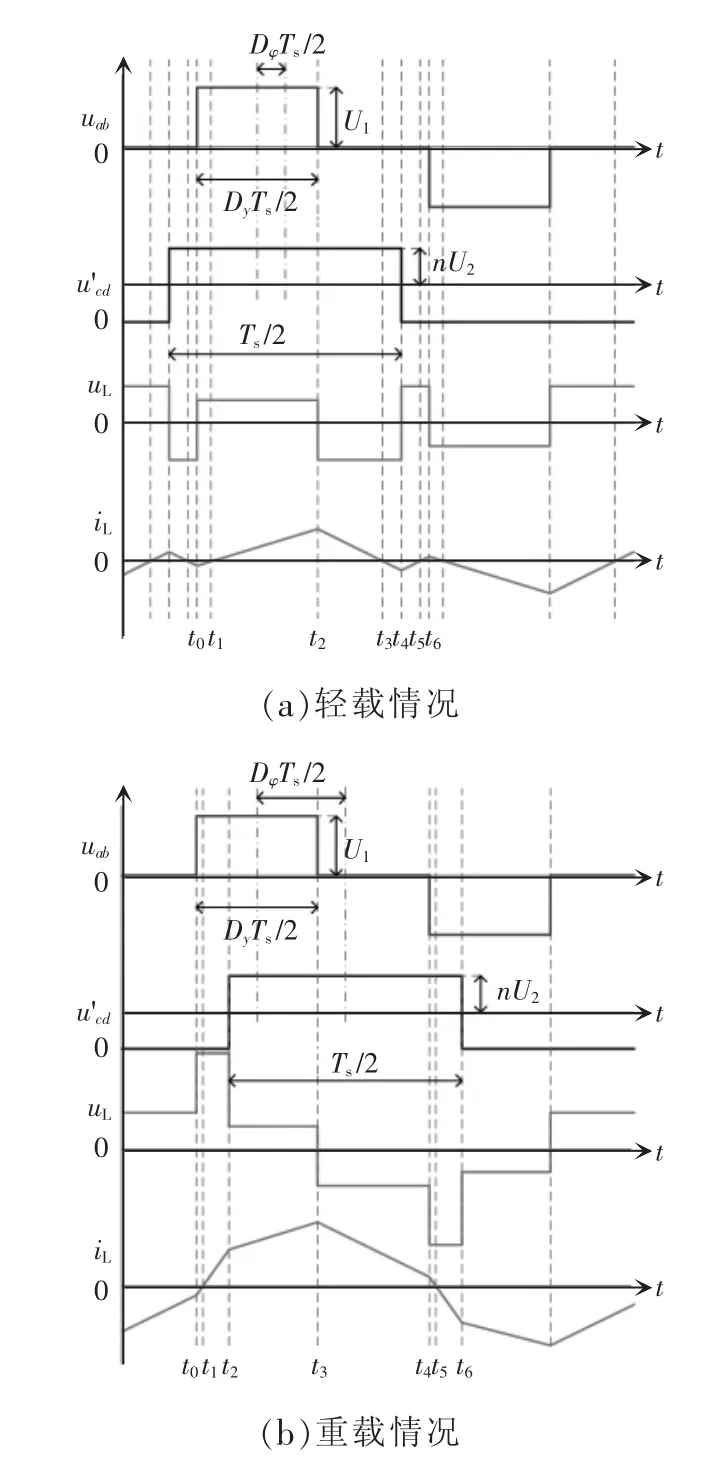
图3 双重移相控制典型波形Fig.3 Typical waveforms of DPS control
图3为双重移相控制典型波形,其中,Ts为开关周期,Dy为高压侧全桥内移相占空比,即S1与S3相位差与π的比值。Dy=0时,S1与S3同步开通,uab有效电压为0;Dy=1时,S1与S3相位相差π,双重移相转变为单移相控制。
2 双有源桥DC/DC变换器工作原理
传统的单移相控制方法,在稳态时,输入、输出电压不变,传输功率大小只与移相占空比Dφ相关;双重移相控制由于加入了内移相占空比Dy,因此传输功率同时受到Dφ与Dy的影响,这使得功率调节的自由度更高。
由于U1=nU2情况下,单移相控制即可实现全负载范围零电压开通,又因为双有源桥电路本身具有对称性,因此本文主要讨论U1>nU2时,对高压侧进行内移相的情况。
对于传统的单移相控制策略,Dφ∈[0,0.5]时,输出功率与 Dφ正相关,而当 Dφ∈[0.5,1]时,输出功率与Dφ呈负相关关系。由于传输相同功率时,Dφ>0.5会产生更大的能量回流,因此通常限制Dφ<0.5。通过文献[11]的分析可知,以上结论对于双重移相控制同样适用,因此本文只讨论 Dφ∈[0,0.5],Dy∈[0,1]的情况。
2.1 双重移相控制工作原理
双重移相控制DAB电路稳态时,uab与ucd上升沿的相位存在两种相位关系,如图3所示,因此功率传输特性需要分两种情况讨论。
文献[8]对双重移相控制的功率传输特性进行了研究,为了方便本文分析,首先将输出功率进行标幺化处理。定义功率基值Pbase为

式中,k=nU2/U1,本文中 k<1,则功率传输方程为

其中,
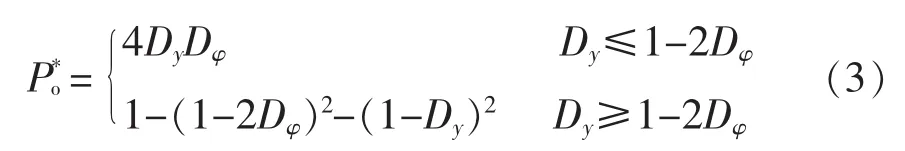
式中,Po和分别为输出功率及其标幺值。由式(3)功率传输特性如图4所示。可以看出,实现相同传输功率,Dφ和Dy可以有多种组合,在实际工作中可以针对回流能量、开关管电流应力、电感电流等因素对Dφ和Dy的关系进行限定,从而实现优化目标。

图4 双重移相控制功率传输特性Fig.4 Power transfer characteristics of DPS control
2.2 软开关范围
与功率传输特性相同,根据uab与ucd上升沿的相位关系,双重移相控制软开关状态也要对轻载与重载两种情况分别进行讨论。
当 Dy≤1-2Dφ时,电路工作波形如图3(a)所示,若不考虑开关过程,则此时各开关管实现软开关的条件如表1所示。

表1 Dy≤1-2Dφ时软开关条件Tab.1 Soft switching requirements when Dy≤1-2Dφ
根据文献[8]给出的电感电流方程,可以给出电感电流在 t0、t2、t4时刻的表达式为

根据式(4)以及表1的软开关条件,可以得出满足所有开关器件零电压开通时Dφ与Dy的关系,即

当 Dy≥1-2Dφ时,电路工作波形如图3(b)所示,此时各开关管实现软开关的条件如表2所示。

表2 Dy≥1-2Dφ时软开关条件Tab.2 Soft switching requirements when Dy≥1-2Dφ
此时,电感电流在 t0、t2、t3时刻的表达式为

同样求解出此阶段满足所有开关器件零电压开通的Dφ与Dy关系为

根据上述Dφ与Dy约束条件,则双重移相控制工作区如图5所示,图中虚线为功率标幺值等高线。根据开关时序,工作区可分为6部分,其中,区域I和区域II为ZVS工作区。

图5 双重移相控制软开关工作区Fig.5 Soft switching range of DPS control
3 双有源桥变换器回流功率分析
由图3(b)可知,在 t0~t1时间段内,电感电流与原边全桥输出电压相位相反,这段时间内电感能量流回原边电容;对于变压器副边,在t1~t2时间段内,电感电流与副边全桥输出电压相位相反,副边能量流回电感。这部分能量均为回流功率。
双重移相控制的双有源桥变换器,根据电感电流波形可以分为6个工作区,如图5所示,各工作区边界条件如表3所示。

表3 双重移相控制工作区Tab.3 Workspace of DPS control
通常在非轻载情况下,为了保证器件ZVS,变换器大多工作在区域I,因此本文以工作区I为例研究功率回流情况。设QPI、QSI分别为原、副边在工作区I的回流功率,有

对式(8)进行求解得
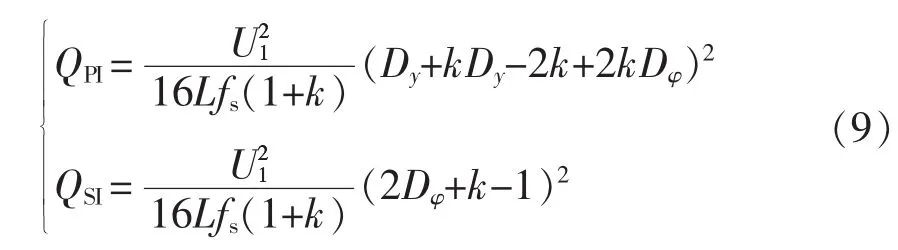
变换器原、副边产生的回流能量使变换器产生无功损耗,传输相同有功功率情况下,回流功率越小,表现为变换器功率因数越高,转换效率也相应提高。因此,本文定义功率因数为

对工作区I~VI分别进行功率因数计算,可以得到功率因数分布曲面,如图6所示。
由计算可得,在6个工作区的交点处(图5中B 点),即 Dφ=(1-k)/2、Dy=k 时,原、副边回流能量均为0,此时变换器功率因数最高,λ=1。
对于传统双重移相控制双有源桥变换器,随着负载的变化需要调节Dφ、Dy以维持功率平衡,因此变换器无法保持在回流功率最低工作点,因此,在保证功率平衡的基础上,选择Dφ、Dy在回流功率尽可能小的工作点有助于提升变换器效率。
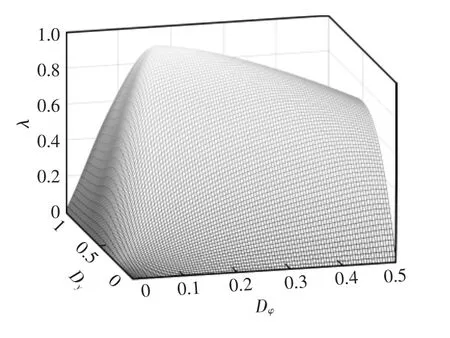
图6 功率因数分布曲面Fig.6 Distribution surface of power factor
本文对软开关工作区(工作区I、II)中不同功率下实现最小回流能量的Dφ、Dy进行求解,得出最小回流能量工作曲线,但由于该工作曲线方程过于复杂,不利于工程应用,因此对该工作曲线进行了线性化处理,即

得到近似最小回流功率工作曲线,如图5实线所示。
4 双有源桥变换器变频移相控制策略
传统的双重移相控制主要通过改变Dφ和Dy来调节功率标幺值,而忽略了开关频率fs对功率基值Pbase的影响。本文在传统双重移相控制的基础上,提出了一种结合频率控制的混合控制策略,减小回流能量,提高系统效率。
对于宽电压范围的双有源桥电路,变压器变比一般选择为额定电压工作点的输入、输出电压比,这有利于在额定工作点达到较高的转换效率,然而当输出电压偏离额定工作点时,系统的回流能量、电流应力等都会出现明显恶化,因此本文主要考虑输入、输出电压不匹配时的回流能量优化。
由前面的分析可知,在最小回流功率曲线上,工作点越靠近最佳工作点(图5中B点),回流能量越小,功率因数也越高,因此可以通过调节开关频率,使变换器工作点向最佳工作点靠近。
实际系统中,B点出变换器工作在临界ZVS状态,开关损耗较大,另外考虑到死区的影响,难以进行精确控制电路工作在该点,因此通常选择将最佳工作点稍作偏移至图5中B1点,在满足回流功率较小的同时较好地实现ZVS,且留有一定余量。
设变换器额定工作频率为fbase,为防止变压器饱和,变频控制的最低频率工作点应保证变压器磁通量不超过额定工作点(设额定工作点k=1),根据变压器磁通计算公式可得

本文提出的变频移相控制策略主要针对输入输出电压不匹配、输出功率较大情况下,即工作区I的回流功率进行优化。在开关频率满足式(12)限定条件下,使移相角Dφ、Dy尽可能接近最佳工作点,当负载变化时,优先通过控制开关频率fs实现传输功率平衡,当fs达到限定值后,维持fs不变,调节Dφ、Dy实现功率平衡。
5 实验验证
为了验证以上控制方法的软开关工作范围,本文搭建了双有源桥DC/DC变换器实验平台,其中串联电感L=40 μH,变压器变比n=13/11,额定工作点如表4所示。

表4 双有源桥变换器额定工作范围Tab.4 Rated operating range of DAB converter
该电路在额定工作点工作时,输入、输出电压匹配度较高,采用单移相控制即可实现约96%的传输效率。本文主要关注输入、输出电压不匹配时的软开关工作情况,因此选择U1=400 V、U2=240 V作为实验工作点,此时k≈0.7,变频移相控制典型测试波形如图7所示。
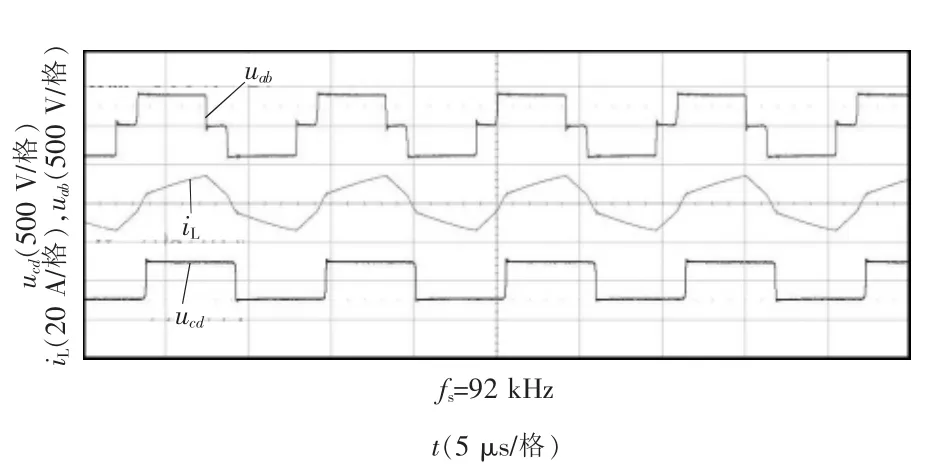
图7 变频移相实验波形Fig.7 Experimental waveforms of variable-frequency phase shift
从图7波形可以看出,电感电流在满足开关管ZVS换流的前提下,回流功率几乎可以忽略。表5给出了10 A输出电流情况下,单移相、双重移相以及混合控制的实验结果。
对于75%负载情况,单移相控制方法将进入硬开关工作区,效率较低,这里不作讨论,双重移相与混合控制实验结果如表6所示。
由实验结果可以看出,在输入、输出电压不匹配情况下,输出功率较大时,混合控制与优化的双重移相控制转换效率均高于传统单移相控制,验证了回流功率对系统效率的影响,当输出功率降低时,双重移相控制器件软开关特性逐渐变差,而混合控制能够在避免工作点过于接近临界点,提高系统效率。
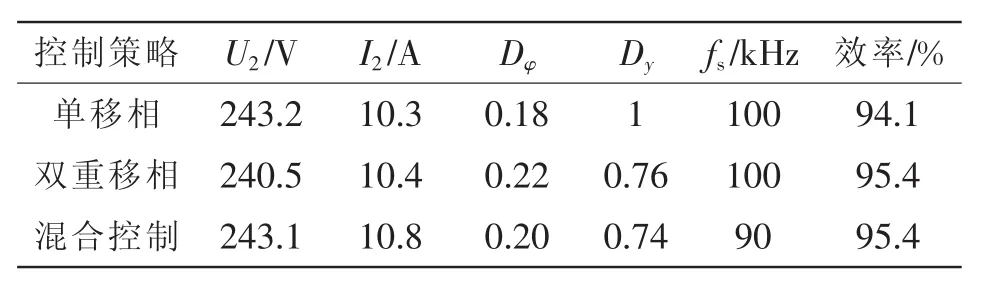
表5 实验平台满载工作点Tab.5 Operating states of full load on experimental platform
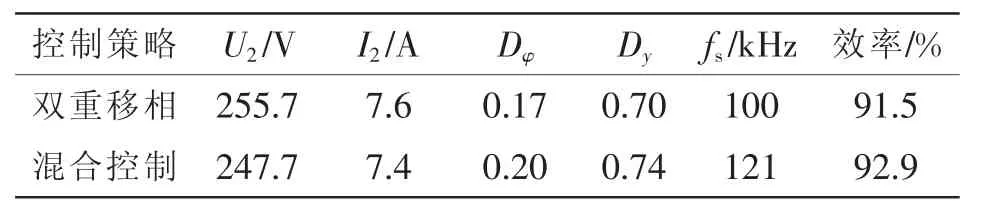
表6 实验平台75%负载工作点Tab.6 Operating states of 75%load on experimental platform
6 结论
本文分析了双重移相控制下双有源桥DC/DC变换器的功率回路现象,以减小回流功率为目标对双有源桥双重移相控制策略进行优化,进一步提出变频移相混合控制策略。本文搭建了3.3 kW实验样机,从理论分析和实验结果可以看到,该控制策略具有以下特性:
(1)减小系统回流功率,通过变频使系统在宽负载范围工作在最佳效率点。
(2)提高了双有源桥变换器的控制自由度,扩展了双有源桥变换器的控制思路。

