基于非对称耦合电感的交错并联磁集成软开关双向DC/DC变换器的研究
杨玉岗,王金海,张书淇,朱恩泽
(辽宁工程技术大学电气与控制工程学院,葫芦岛125105)
现今社会科技的繁荣发展,双向DC/DC变换器 BDC(bidirectional DC/DC converter)的实际应用也随之逐渐增多,在众多应用场合中特别是直流不间断电源系统(DC-UPS)、航天电源系统(aerospace power system)、电动汽车(electric vehicle)、直流功率放大器(DC power amplifier)及蓄电池储能 BESS(battery energy storage system)等场合的应用较为突出,从而对BDC的工作效率、设备体积和损耗等方面的要求也逐步严格[1-5]。在实际应用中随着对BDC功率级别的要求逐步提高,为了满足应用需求,国内外均有学者提出在变换器中采用交错并联技术,也即在BDC硬件单一拓扑的基础上采用多个传统双向DC/DC电路进行空间并联,以减小每通道中的电流应力和传输功率;同时,在时域上使得变换器主开关管的导通时间相互交错,通过变换器各相电流的相互叠加,成倍提高开关变换器的等效开关频率,减小变换器输入侧电流纹波和输出侧的电流、电压纹波,可有效减小输入侧、输出侧的滤波电容容量及其体积[6-8]。
在电路中采用交错并联的拓扑结构可以解决BDC中大功率的问题,然而也会相应地导致变换器中磁性元件数量的骤增,增大了BDC的体积、重量及成本。为了解决这一问题,引入磁集成技术是十分必要的,即将多个磁性元件集成为1个,在减小磁性元件体积的同时,有效减小稳态相电流纹波,提高暂态响应速度。采用交错并联技术带来的另一个问题就是变换器的开关管数量增多与开关频率的升高,均增加了损耗。若可以使BDC的开关管实现零电压开关 ZVS(zero-voltage switch)控制,那么就会大大减小其开关损耗,提高工作效率。所以ZVS技术应运而生,成为当前电力电子技术的一个研究热点[9-15]。
1 双向DC/DC变换器的电路拓扑
本文以4相Buck+Boost交错并联磁集成BDC变换器为例,研究变换器在Buck模式下ZVS的实现。4相Buck+Boost交错并联磁集成BDC变换器的拓扑结构如图1所示。
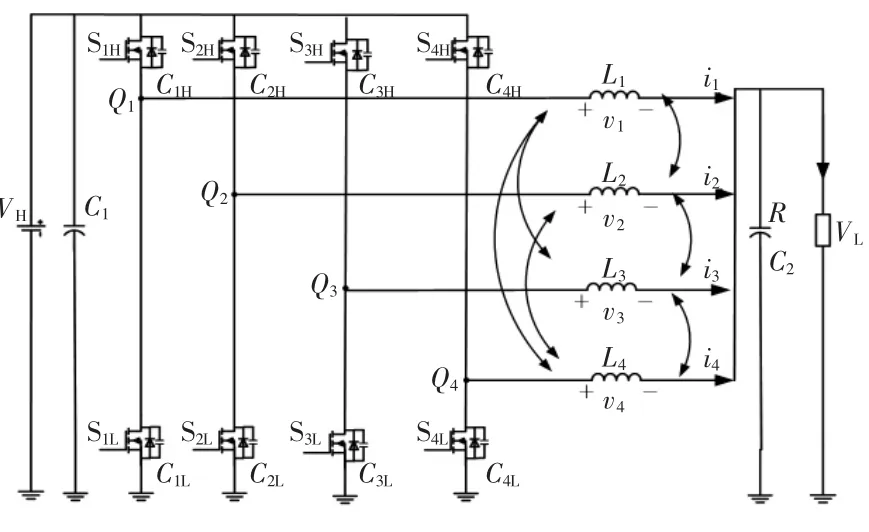
图1 4相交错并联磁集成BDC拓扑结构Fig.1 Topology of 4-phase interleaving parallel magnetically integrated BDC
图1中:VH和VL分别为变换器高、低压侧的电压,R为负载电阻,v1~v4分别为加在4相非对称耦合电感器绕组上的电压;i1~i4分别为流过4相非对称耦合电感器绕组的电流。S1H~S4H分别为每相半桥结构的上管开关管,S1L~S4L分别为每相半桥电路结构的下管开关管,C1H~C4H、C1L~C4L分别为对应相开关管的输出电容;L1、L2、L3和 L4分别为 4相非对称耦合电感器绕组的自感,Mij(i,j=1,2,3,4)为各相电感绕组之间的互感,本文采用4相非对称反向耦合的电感器,Mij<0。通常,4相非对称耦合电感器的第1相和第4相、第2相和第3相电感参数分别相等,且规定第1、4相电感值小于第2、3相电感值,即(L1=L4)<(L2=L3),M12=M13=M24=M34≠M23≠M14;设k为这种4相非对称耦合电感器的非对称度;k1为第 1、2相之间,第 1、3相之间,第 2、4相之间及第3、4相之间的耦合系数;k2为第1、4相之间的耦合系数;k3为第2、3相之间的耦合系数,分别满足以下条件

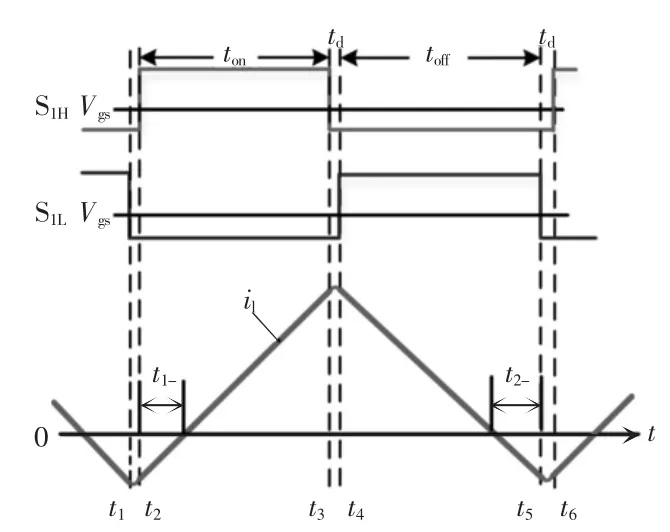
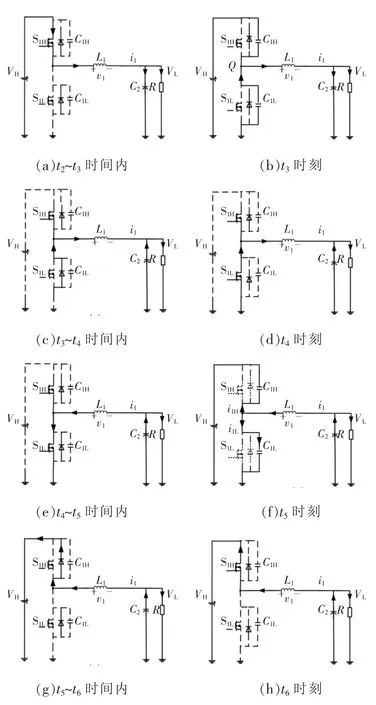
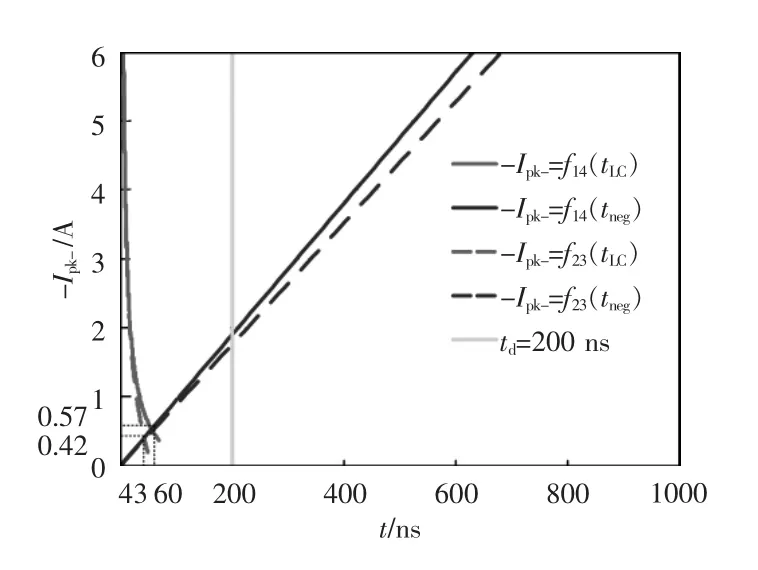
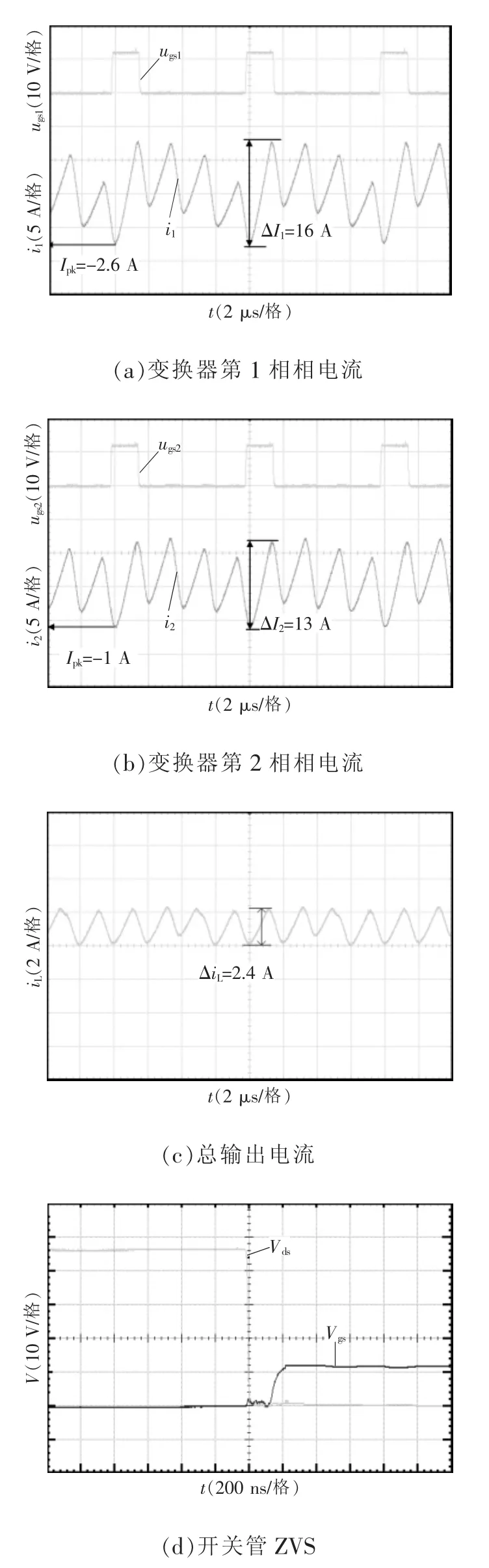
并有 0 在Buck模式下,单通道BDC的电路拓扑如图2所示,说明其变换器进行ZVS控制的工作原理。图中,上管S1H和下管S1L分别为主开关管和副开关管。 图2 单通道变换器的拓扑Fig.2 Topology of single-channel converter 如图3所示,为变换器ZVS的两个开关管驱动波形及电感电流波形,其工作过程如图4所示。图4(a)~(d)为副开关管 S1L的控制过程,图4(e)~(h)为主开关管 S1H的控制过程。图4(a):在 t2~t3时间段内,上管S1H导通,C1H两端电压为0,S1L关闭,C1L两端电压为 VH,即 Q 点电压为 VH;图4(b)t3时刻S1H关闭,C1L放电,C1H充电,Q 点电压下降;图4(c)若死区时间td足够,C1L两端电压会一直下降,在t4时刻之前S1L的体二极管开通,S1L漏源极两端的电压近似等于 0;图4(d)在 t4时刻打开 S1L,实现S1L的零电压开通;图4(e)t4~t5时间段内,S1L开通,S1H关闭,C1L两端电压始终为0,C1H两端电压为VH,Q点电压为0,电感放电,电流下降并反向;图4(f)在t5时刻S1L关闭,电感释放能量,使得C1L充电,C1H放电,Q点的电压上升;图4(g)若td足够,反向的电流足够大,那么Q点的电压会持续上升,在t6时刻之前S1H的体二极管导通,S1H漏源极两端的电压近似为 0;图4(h)在 t6时刻打开 S1H,实现 S1H的零电压开通,t1~ t2时刻重复 t5~t6时刻的过程。 图3 单相导通时电感电流的波形Fig.3 Waveform of inductor current in the case of single-phase conduction 综上分析可知,副开关管在实现ZVS时不需要让电流反向,只需要死区时间合适,副开关管的漏源极寄生电容和电路电感谐振,让寄生的体二极管开通,ZVS就能实现。当电流在连续模式CCM(continuous conduction mode)或者在断续模式DCM(discontinuous conduction mode)时,副开关管的 ZVS都是能实现的,而主开关管ZVS的实现,死区时间要足够,反向的电流要足够,也即必须在DCM下才能实现。由于电感的不对称性,分析单相时,需对耦合电感的第1相及第2相分别进行讨论。 当只有第1相开通工作时,电感的电流纹波为 图4 ZVS控制下单通道BDC的等效电路Fig.4 Equivalent circuit of single-channel BDC under ZVS control 式中:fs为变换器的工作频率;D为占空比设变换器的总输出电流的平均值是Io,则反向峰值电流Ipk-为 在一个周期内,电感电流小于0的持续时间为 同理,当只有第2相开通工作时,一个周期内电感电流小于0的持续时间为 在t1~t2死区时间内变换器第1相的工作状态如图4(f)所示,波形如图3所示,i1H和i1L分别为电容C1H和C1L上的电流,在死区时间内电感L1的电压方程为 电容电压方程为 整理得 设在最初时刻,电感电流的初始值为i0,联立式(5)与式(7)得 当v1L=VH时,电容C1L、C1H与电感L1的谐振完成,振荡时间为tLC。只有当td>tLC才能实现ZVS,又由于谐振电容很小,是皮法级别,谐振时间很短,可以认为 i0≈-Ipk-,从而得到 依据以上推理过程,当只有第2相工作时可得 综上,单相工作时,ZVS的实现,需要同时考虑反向峰值电流以及死区时间的影响,则第1相或第4相实现ZVS的条件为 同理,第2相或第3相实现ZVS的条件为 为保持电感器尽可能地对称,两相导通时使耦合电感第1、4相工作或第2、3相工作,且两相之间的相位差为π/2。当变换器第1、4相工作时,占空比D<1/4时的模态如图5所示。 图5 两相交错并联磁集成BDC的工作模态Fig.5 Working modes of 2-phase interleaving parallel magnetically integrated BDC 利用模态分析方法,可以得到变换器在各个模态下的等效电感,即 式中,D'=1-D。 同理当第2、3相工作时,模态分布与图5类似。利用模态分析方法,可以得到变换器在各模态下的等效电感为 当只有两相工作时,由于1、4相对称,2、3相对称,所以只分析第1、2相即可。第1相的反向电流峰值为 在一个周期内,电感电流小于零的持续时间为 同理,当第2、3相开通工作时,一个周期内第2相电感的电流小于0的持续时间为 在死区时间内,电感电流的波形如图6所示。 两相工作时ZVS的实现过程与单相工作时ZVS实现过程完全相同,则L1和L4电感上的电压方程为 在死区时间 t1~t2内 联立式(18)和式(19)可以得到 电容电压方程为 图6 死区时间对两相交错并联磁集成BDC的影响Fig.6 Effect of dead time on 2-phase interleaving parallel magnetically integrated BDC 整理式(21),可以得到 设在最开始的时刻,电感电流的开始值为i0,联立式(20)与式(22)解得 同样地,当 v1L=VH时,电容 C1L、C1H与电感 L1的谐振完成,振荡时间为tLC,只有当td>tLC时才能实现ZVS,又由于谐振电容很小,是皮法级别,谐振时间很短,可以认为 i0≈-Ipk-,从而得到 根据以上推理过程,当第2、3相工作时得到 综上,ZVS的实现,需要同时考虑反向峰值电流以及死区时间的影响,则第1、4工作时相实现ZVS的条件为 同理第2、3相工作时,实现ZVS的条件为 由于电感器第1、4相对称,第2、3相对称所以只分析第1、2相即可,4相全工作时电路拓扑见图1,第1相模态如图7所示。由图7可见,4相变换器全处于工作状态时各相电感电压在一个周期内的变化情况。 变换器在占空比小于1/4时,一共有8个工作模态,va=VH-VL,vb=-VL,ΔI1为第 1 相电流纹波,利用模态分析方法,可得各模态下的等效电感为 图7 4相交错并联磁集成BDC的工作模态Fig.7 Working modes of 4-phase interleaving parallelmagnetically integrated BDC 由图7可知,第1相电感电流纹波为 第1相电感的等效稳态电感Leq11可表示为 同理,第2相电感电流纹波为 第2相电感的等效稳态电感Leq23可表示为 设变换器的输出电流的平均值为Io,则第1相电感的反向电流的峰值为 依据式(28)得电感电流小于0的时间为 同理,第2的相电感电流反向峰值为 电感电流小于0时间为 在死区时间内,电流波形如图8所示。 ZVS实现过程与单相相同,这里不再赘述。以第1相为例,在死区时间t1~t2内电感电压的方程为 在死区时间 t1~t2内 联立式(37)和式(38),得 图8 死区时间对四相交错并联磁集成BDC的影响Fig.8 Effect of dead time on 4-phase interleaving parallel magnetically integrated BDC 电容电压方程为 整理式(40)得 设在最开始的时刻,电感电流的初始值为i0,联立式(39)与式(41),得 当v1L=VH时,电容C1L、C1H与电感L1的谐振完成,振荡时间为tLC,只有当td>tLC时才能实现ZVS,又由于谐振电容很小,是皮法级别,谐振时间很短,可以认为i0≈-Ipk-,从而得到 同样,依据以上推理过程,当v2L=VH时,电容C2L、C2H与电感L2的谐振完成,振荡时间为tLC,只有当td>tLC时第2相才能实现ZVS 综上,ZVS的实现,需要同时考虑反向峰值电流以及死区时间的影响,则第1、4相导通条件为 第2、3相导通条件为 4相全工作时需同时满足式(45)和式(46)。 本文设计的变换器采用K60单片机+FPGA作为控制芯片,对变换器的输出电压进行采样用于闭环控制,对于输出电流进行采样。图9给出了基于单片机和FPGA的四相交错并联磁集成BDC的系统控制结构。 图9 系统控制结构Fig.9 Structure of system control 实验条件为:VH=48 V,VL=7 V,占空比 D=0.146,4 相耦合电感 L1=L4=4.28 μH、L2=L3=6.3 μH,k=0.68,k1=-0.367,k2=-0.024,k3=-0.33,开关管上管为AON6246,其漏源极间输出电容C1H=258 pF,下管为AON6242,其漏源极间输出电容典型值为540 pF,死区时间td=200 ns。将以上参数代入式(45)和式(46),分别可以得到 4相全工作时需同时满足式(47)和式(48),反向峰值电流与谐振时间,反向电流的时间以及死区时间的关系如图10所示。图中,-Ipk-=f14(tLC)、-Ipk-=f14(tneg)为第 1、4 相反向峰值电流与谐振时间,电流反向时间的关系,-Ipk-=f23(tLC)、-Ipk-=f23(tneg)为第2、3相反向峰值电流与谐振时间,电流反向时间的关系,td表示死区时间。公式取交集即为4相全工作时ZVS实现条件,由图10可见,满足公式约束条件的最小反向峰值电流为-0.57 A,此时谐振时间同样满足约束条件。 确定Ipk-后,可以根据式(33)得到输出电流Io与工作频率fs之间的关系。则第1相或第4相工作时以及第2相或第3相工作时,Io与fs之间的关系分别为 图10 四相交错并联磁集成BDC的ZVS实现条件Fig.10 ZVS conditions for 4-phase interleaving parallel magnetically integrated BDC 4相工作时Io与fs之间的关系如图11所示。 采用4相非对称耦合电感的交错并联磁集成BDC的实验电路如图12所示。电流波形测试采用闭环霍尔电流传感器CHB-25NP,其匝比为n=1/1 000,测试电阻R=1 kΩ,通过示波器测试的电流i=u/(nR),其中u为示波器显示电压值,实验波形如图13所示。 要想实现ZVS,关键在于相电流峰值的选取,经试验测得第1相和第2相的Ipk-分别为-2.6 A和-1 A,理论推导出的第1相和第2相的Ipk-分别为-2.622 A和-1.016 A,其误差分别为0.84%和1.6%。通过对比实验值和理论值可知公式推导的正确性。实现ZVS控制时BDC的效率曲线如图14所示。从图14可以看出,采用ZVS控制可以明显地提高变换器的效率,从而证明了提出控制方案的有效性。 图11 4相工作时Io与fs关系Fig.11 Relationship between output current and switching frequency in the 4-phase operation 图12 实验电路系统Fig.12 Experimental circuit system 图13 实验波形Fig.13 Experimental waveforms 图14 实现ZVS控制时BDC的效率曲线Fig.14 Efficiency curves of BDC under ZVS control 本文分析了交错并联磁集成技术在DC/DC变换器中的应用及ZVS的实现方法。推导了单相、两相、4相交错并联磁集成双向 DC/DC变换器 ZVS的实现条件,分析了实现条件下需要考虑的问题,通过实验的方法验证了理论推导的正确性。2 单相导通时ZVS实现条件

2.1 单相BDC的电感电流反向持续时间




2.2 死区时间对单相BDC的影响



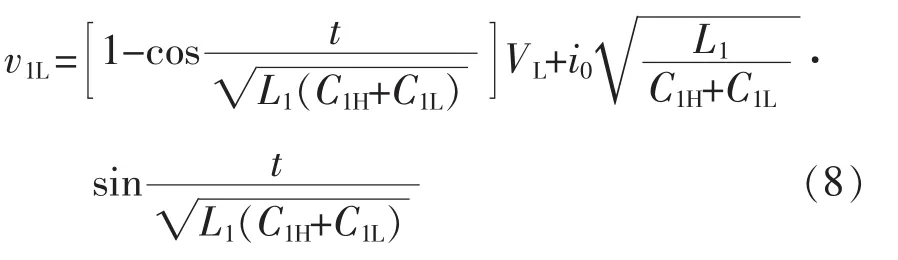
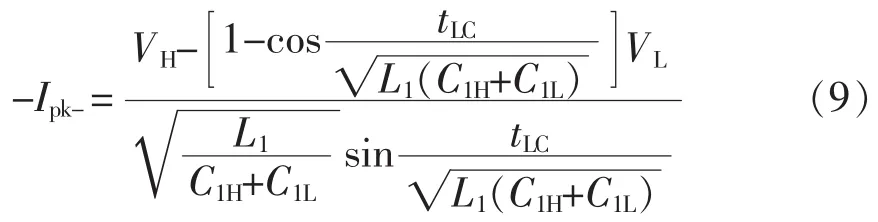

2.3 单相导通时ZVS的实现条件

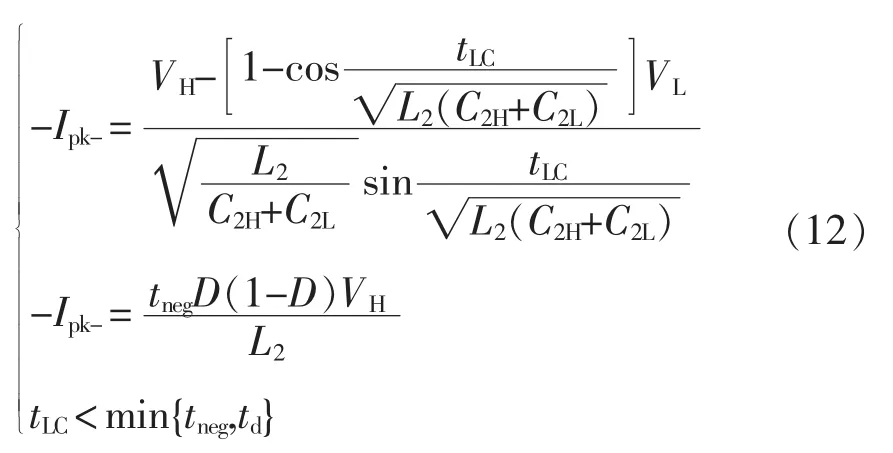
3 两相导通时ZVS实现条件


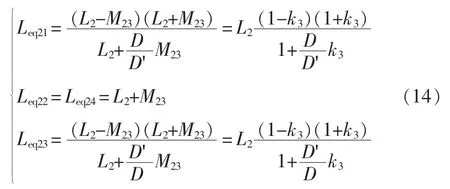
3.1 两相BDC的电感电流反向持续时间
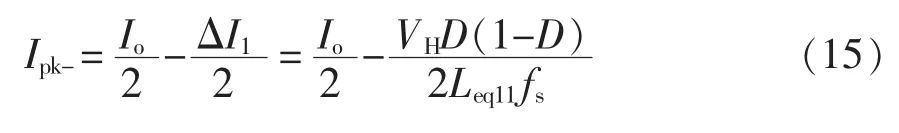
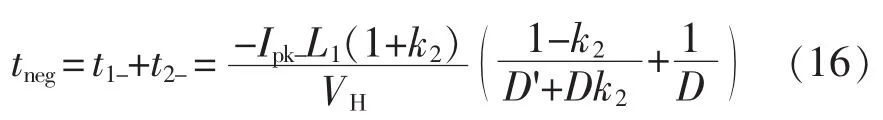
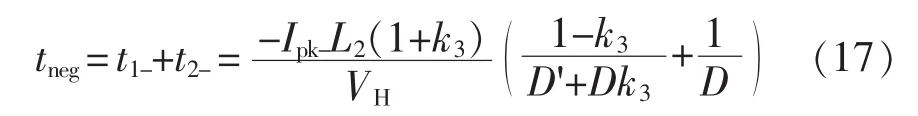
3.2 死区时间对两相BDC的影响


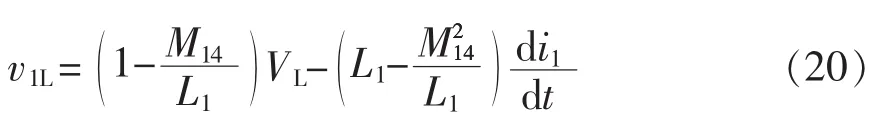

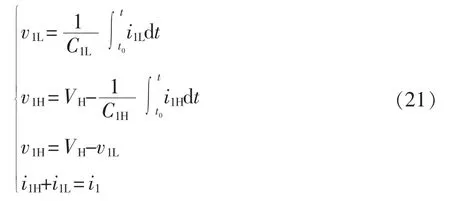


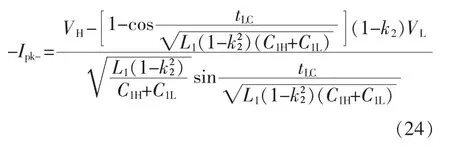
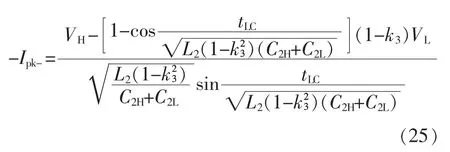
3.3 两相导通时ZVS的实现条件


4 四相导通时ZVS的实现条件
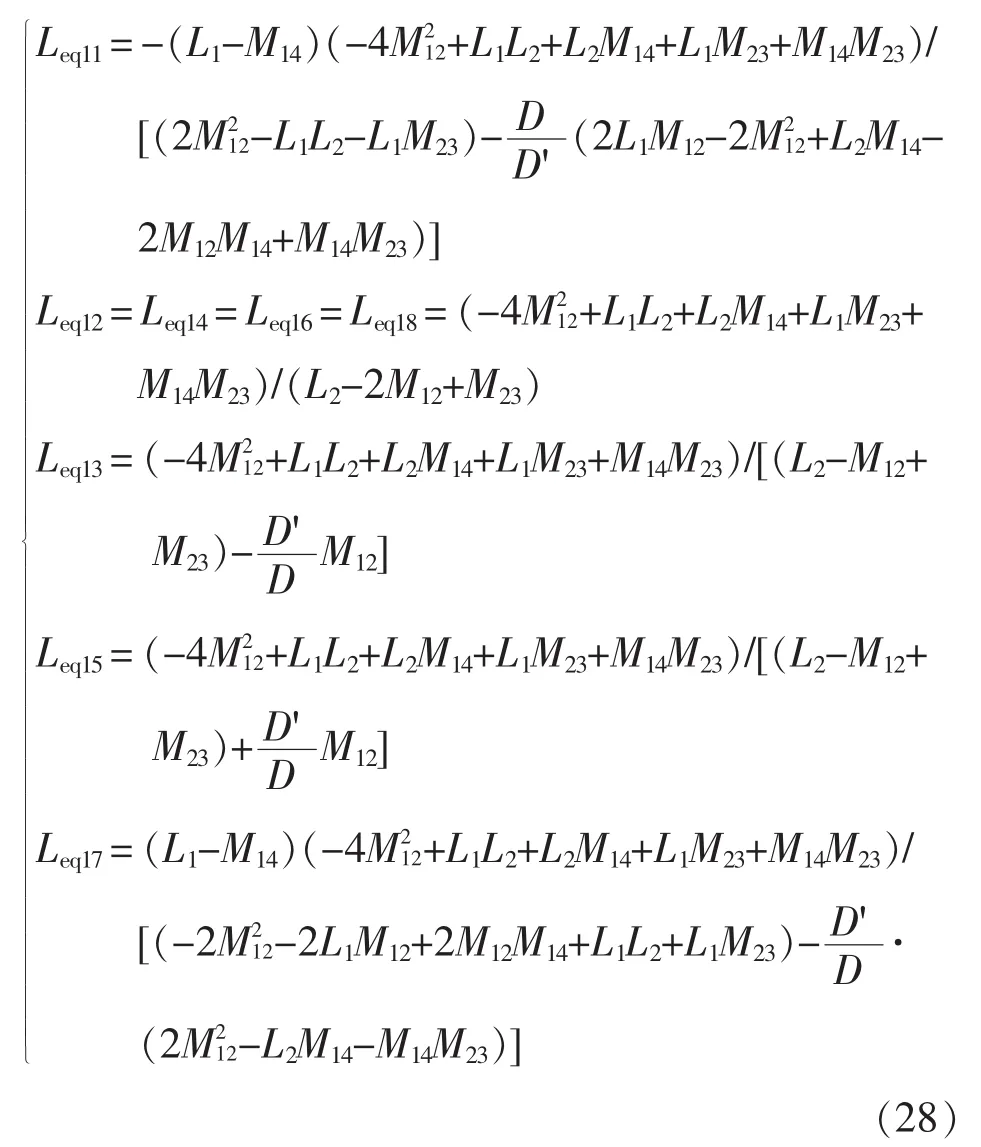


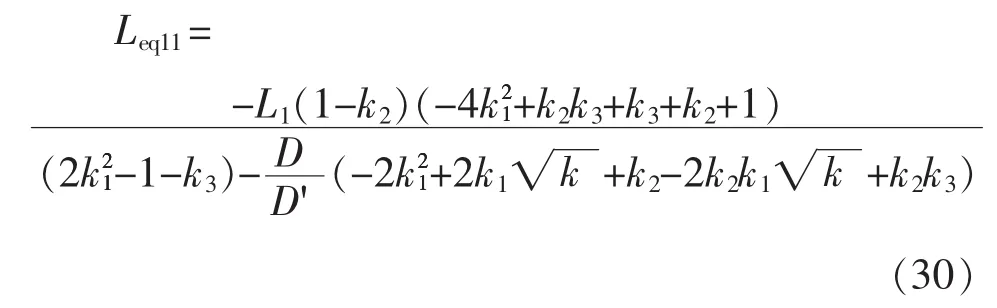

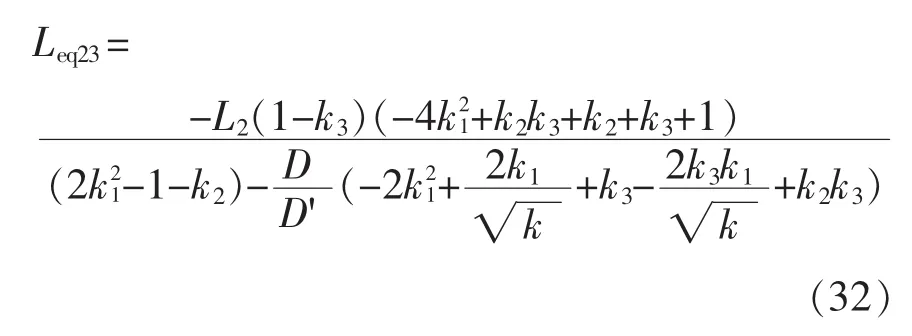
4.1 4相BDC的电感电流反向持续时间
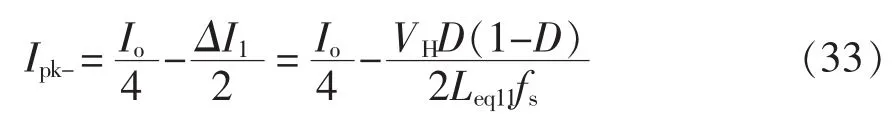
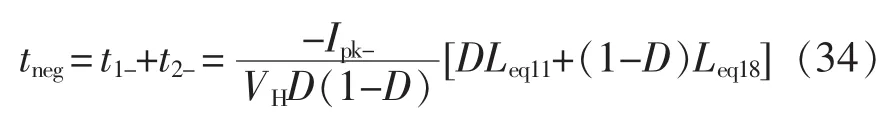

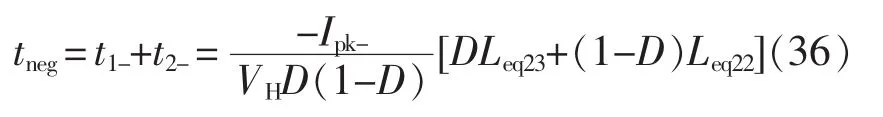
4.2 死区时间对4相BDC的影响


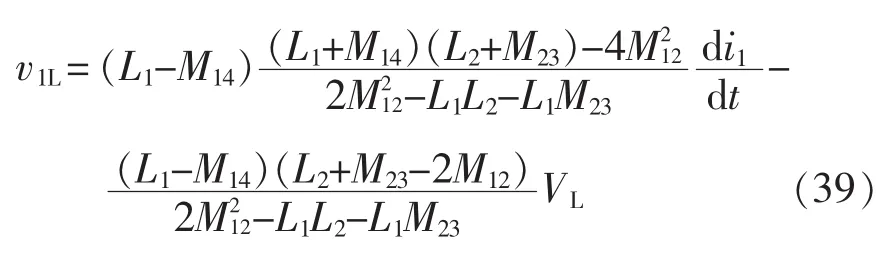
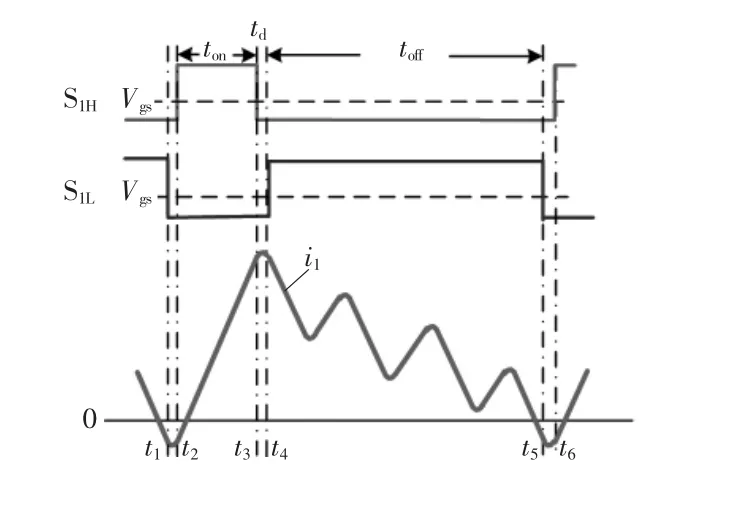
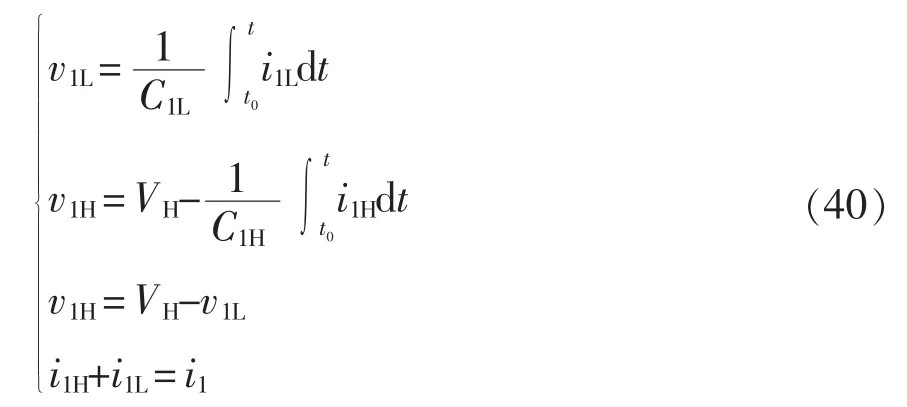




4.3 4相导通时ZVS的实现条件


5 4相交错并联磁集成BDC的系统控制结构

6 实验验证
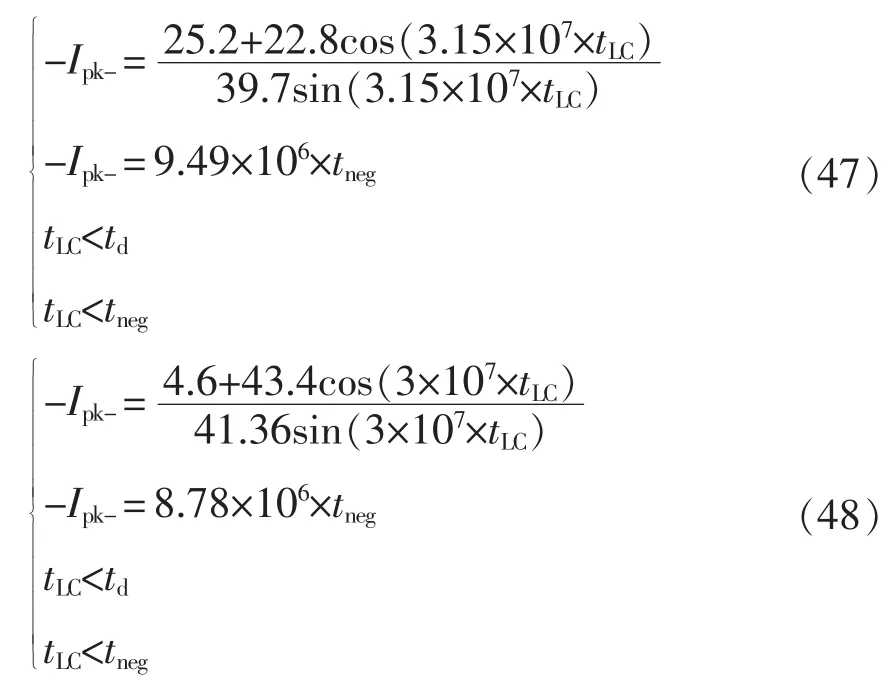




7 结语

