基于虚拟同步机运行模式的平滑算法
马铱林,杨 欢,何绍民
(浙江大学电气工程学院,杭州 310027)
随着能源枯竭和环境污染等问题日益严重,风能、太阳能等分布式可再生能源得到广泛关注。发展分布式发电 DGs(distributed generations)有望实现能源结构优化[1],但也可能会给配电网带来新的挑战。在实际应用中,DGs通常以并网逆变器作为清洁能源与配电网的接口,采用电流控制模式,动态响应迅速[2]。但随着分布式发电渗透率的提高,会导致接入了大量DGs后的配网等效转动惯量相对不足,从而降低其应对功率扰动的能力;并且对于稳定性较差的微网,DGs也难以提供必要的阻尼,使其暂态时的波动加剧,这极大地限制了分布式发电的推广与应用[3-5]。考虑到传统同步发电机对电网天然友好,具有较好的惯性和阻尼特性,若能够使逆变器输出特性模拟同步发电机,将极大改善DGs缺乏惯性和阻尼的现状。基于这一理念,国内外学者提出虚拟同步发电机VSG(virtual synchronous generator)技术,将同步机的数学模型纳入到逆变器控制策略中,模拟逆变器具有传统同步机外特性[6-7],从而减轻电网调节负担。
实际,虚拟同步机的惯量与阻尼特性仍需要能量支撑才能实现。对此,风力发电主要关注于风机的转子动能,既可以通过变流器最大功率点追踪MPPT(maximum power point trace)控制“隐藏”出力,也可以通过VSG控制策略将转子动能额外释放用于频率调控[8-9]。对于光伏发电,除电容以外再无储能单元,因而难以像风机一般提供旋转备用,通常会在逆变器直流侧增设适当容量的储能系统ESS(energy storage system)[9],以提供功率备用。
但是,储能系统的功率与储能容量等物理边界会因环境和投资等因素有所限制,VSG的运行特性也因此受到这些物理约束的影响。选择合适的储能单元,不仅可以使系统获得理想的工作性能,还能够节约经济成本[2]。对此,已有大量的研究工作对储能系统的边界问题进行了分析。文献[11]基于VSG数学模型,提出了对储能单元的功率和能量等参数的优化配置方法,文献[12]在文献[11]的基础上,通过仿真和实验验证其所提配置方法的有效性;文献[13]则从系统极点的角度出发,探讨了输出无功功率对储能物理约束的影响;文献[14]选用铅酸电池作为储能单元,并基于其充放电特性以及储能物理约束,对VSG的稳定运行区域进行了讨论。
上述文献涉及储能系统边界的诸多问题,但尚未围绕储能系统的充放电功率变化率约束展开讨论。因为在实际应用中,储能系统多采用化学介质进行能量存储[15]。当光伏出力剧烈波动或电网负荷功率骤变时,倘若不对储能功率变化率进行限制,其可能超出储能系统内部化学反应的变化速率,使得系统内部局部过充或过放[16],甚至可能会造成热失控,引发爆炸或起火[17],造成安全隐患。与此同时,即便储能功率变化率在安全范围内,高充放电倍率下储能系统的功率循环次数也会显著减少,缩短储能单元的使用寿命[18]。对此,可以在系统中加入平滑(smoothing)算法,保障系统安全可靠运行[19]。平滑算法是指通过降低反馈到控制系统的功率波动变化率,减缓储能单元充放电功率变化与充放电频率(次数)的算法。其效果主要体现在减小短时间内源荷功率波动对系统产生的影响,保护储能单元。但它也会改变系统输出特性,从而引起储能系统的功率与储能容量等物理边界发生变化。
基于上述问题,本文以光伏发电为例,主要围绕平滑算法对储能系统物理约束以及虚拟同步机系统提供无功能力的影响进行了详细讨论。首先,本文对光伏储能系统以及VSG控制策略进行了建模,并以此为基础建立考虑平滑算法的小信号模型;然后,基于该模型讨论当系统参数(虚拟转动惯量J、阻尼系数D)固定时,平滑单元对储能系统的功率变化率、能量、功率和响应时间等主要物理约束的影响;并且当储能容量固定时,进一步探究了平滑单元对系统提供无功能力的影响;最后,使用PSCAD/EMTDC验证所提结论的正确性及有效性。
1 光伏储能系统及其虚拟同步机控制
本文讨论的光伏储能系统拓扑结构与虚拟同步机等效示意如图1所示[20]。系统直流侧的储能系统以及光伏阵列分别通过DC/DC变换电路并联到直流母线,又通过母线电容Cdc,由三相逆变电路将直流电压或电流变换为开关脉冲量,再经过低通滤波电路,将滤除高频分量的交流量输出到电网。
为了充分利用可再生能源,需要对光伏阵列进行MPPT控制[21];储能系统所接的变换器为双向DC/DC变换电路,该电路可以控制储能系统的充放电,以提供系统所需的惯性。
图1中,Lg为电力系统内部等效阻抗(主要为感性),其与滤波电感L、滤波电容C共同构成了等效的LCL型滤波电路[22];RD为阻尼电阻,用于阻尼滤波器的自然谐振分量[23];R为线路等效电阻。

图1 光伏储能系统与虚拟同步机等效示意Fig.1 Equivalent schematic of photovoltaic energy storage system and virtual synchronous generator
虚拟同步发电机的控制思想,是基于储能系统提供的功率支撑,从而模拟传统同步发电机的惯性与阻尼特性。借鉴同步发电机的二阶模型,可以得到电流控制型VSG控制策略,如图2所示。网侧负荷变化会引起电网频率改变,反馈到系统中就是频率下垂功率;为了减少光伏出力以及电网负荷波动对储能系统产生的不利影响,采用经过平滑算法后的功率作为VSG系统有功出力参考值;在静止坐标系下,选用准比例谐振QPR(quasi proportional resonance)控制实现电流对其指令的无静差跟踪。
图2中,J为虚拟转动惯量;D为阻尼系数;kf、kq、kv分别为调频系数、无功调节系数和电压调节系数;ω为虚拟机械角速度;ω0为同步角速度;f为电网频率,通过锁相环得到;E0为VSG空载电势;E为VSG内电势幅值;U为VSG机端电压的实际有效值;Q为VSG机端输出无功功率;Uref、Qref分别为电压和无功功率的给定值;uabc为VSG机端电压;iabc为逆变器输出电流。
基于传统同步发电机的数学模型,VSG控制策略相应包含有功调节、无功调节、运动方程以及电磁方程等环节。其中,有功无功调节均采用下垂控制,运动方程为同步机经典二阶运动方程,电磁方程则实际为电压电流计算方程。
2 储能单元边界研究
2.1 考虑平滑算法的小信号模型
如图2所示,有功出力参考值是光伏阵列的输出功率以及频率下垂功率经过平滑算法,降低波动变化率后得到的。目前已有许多关于平滑控制方法的研究,如:一阶低通滤波法、限制最大爬坡率法以及移动平均法等[24]。本文采用的是一阶低通滤波法,该方法平滑性能较好,且易于频域分析。由此可得该平滑环节的标幺值小信号模型,即
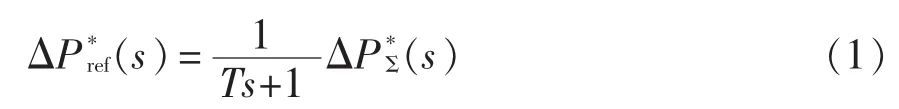
为模拟惯性和阻尼特性,通常采用传统同步发电机的经典二阶运动方程进行VSG控制,即
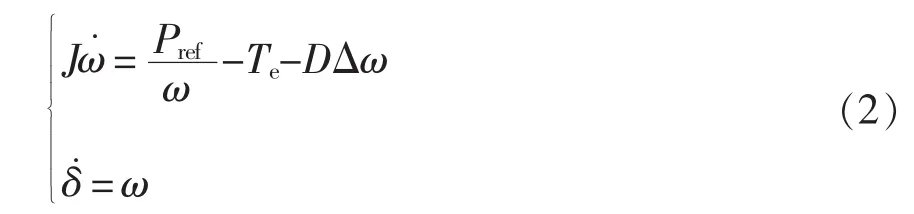
式中:δ为功角;Te为电磁转矩,可由VSG输出有功功率Pe计算得到。
将式(2)两边都除以转矩基准 TB=Sn/ω0,化简可得运动方程的标幺值模型为

式中:ωr为转差标幺值,ωr=(ω-ω0)/ω0;Dp为阻尼常数为惯性时间常数。
基于式(3),进行拉氏变换,可得运动方程的复频域小信号模型为

式中,SE为同步功率,可由有功功率Pe对功角δ求解偏导数得到,即

式中:Es、δs分别为系统处于稳态, 即 Pe=Pref、Qe=Qref时,VSG的虚拟感应电势和功角;Z为线路阻抗;α为阻抗角,二者分别为

综合式(1)和式(4),可整理得到考虑平滑算法的VSG运动方程小信号模型,如图3所示。
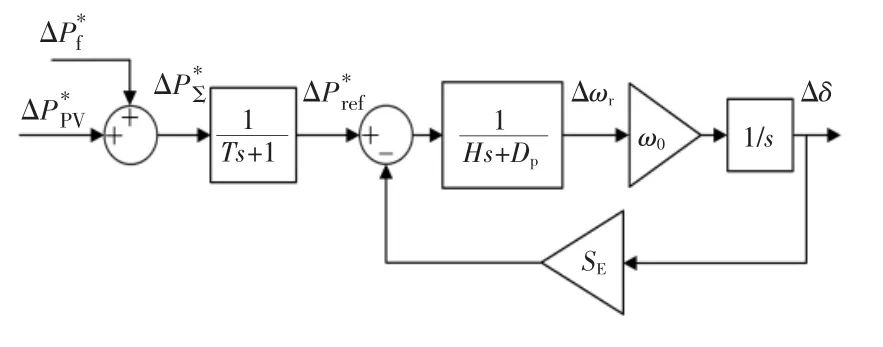
图3 VSG小信号模型Fig.3 Small-signal model of VSG
稳态时,指令功率恒定,平滑环节相当于放大倍数为1的比例环节。此时系统即为传统的VSG系统,谐波畸变率、输出功率误差等稳态指标并未因平滑算法的加入有所变化。
传统VSG运动方程的小信号模型属于二阶系统,整理可得有功出力参考值与有功功率经典二阶传递函数,即

式中:ωn为自然角频率;ξ为阻尼比。二者分别表示为
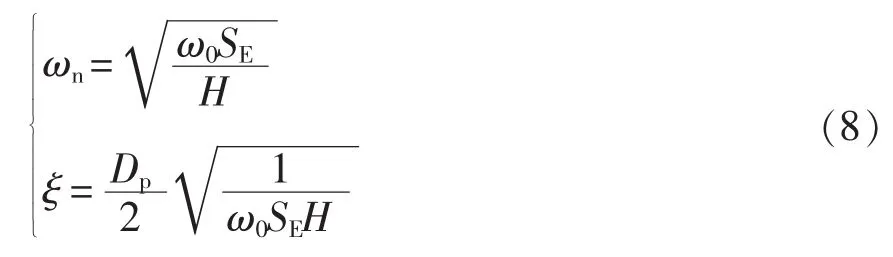
为了使得系统具有较快的响应与较小的超调,可以设计VSG的阻尼比为ξ∈(0.7,1)。
目前已有许多研究讨论了式(7)的储能物理约束,即控制参数H、Dp与储能系统各物理指标的对应关系。而本文讨论的控制系统,在有功出力参考值前增加了一阶低通滤波环节,平滑光伏出力以及电网负荷的波动,从而降低储能功率变化率的约束条件,保护储能系统使用寿命。下面,本文将结合前述系统的阶跃响应,验证控制参数固定时,平滑算法的加入可以降低储能功率变化率;再以此为基础,探究平滑算法对其他物理指标(储能容量、输出功率以及响应时间)的影响。
2.2 平滑算法对储能功率变化率的影响
本节讨论的平滑算法输入量,实际为光伏出力以及频率调节功率的代数和。为便于讨论,不妨将指令功率视为主体,忽略其内部功率数值关系,仅考虑其代数运算后的输出特性。整理式(1)和式(7),可得此时系统的传递函数为

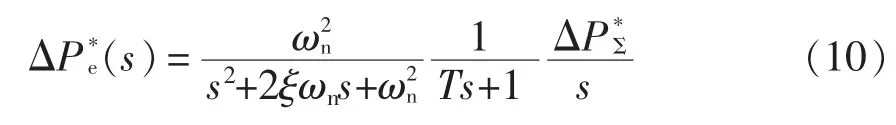
对式(10)进行拉氏反变换,可得系统响应时域表达式为
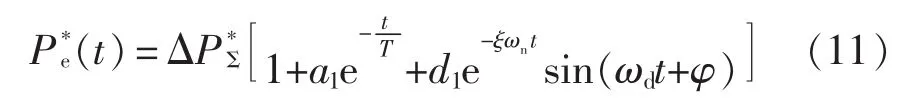
其中,各系数分别为
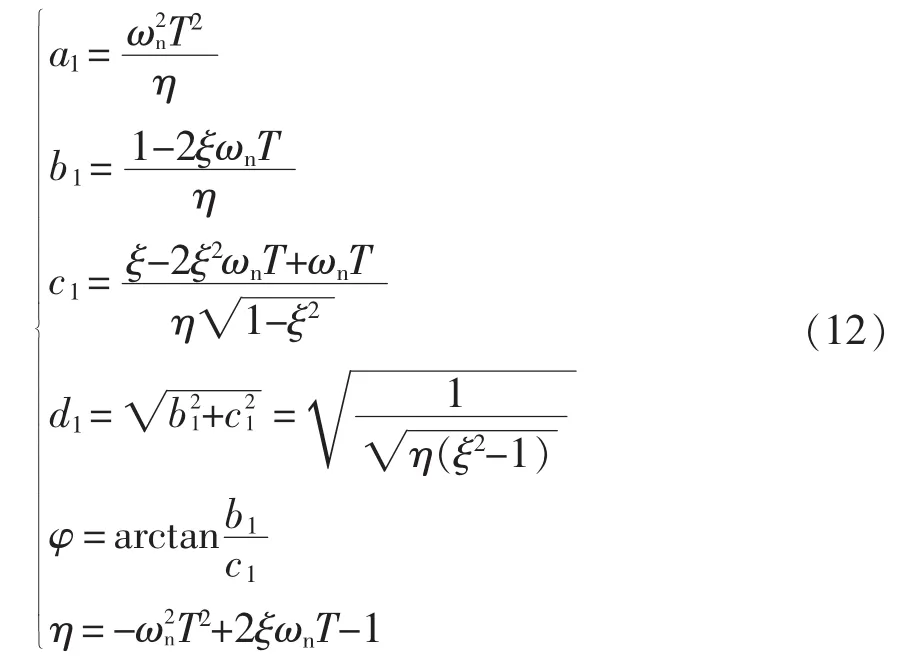
由式(11),输出功率的时域波形如图4所示。基于前文所述,指令功率可以视作光伏出力与频率调节功率的代数和。其中,频率调节分量为系统控制量,反映电网负荷情况,与光伏出力无关,其所需功率全部由储能系统提供。由此可以推断:储能系统实际的吸收功率为光伏出力与系统输出功率的差值,即
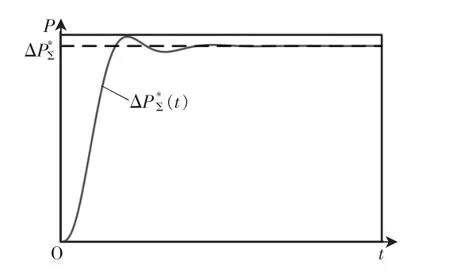
图4 光伏出力阶跃时的功率响应Fig.4 Power response to step change in photovoltaic output
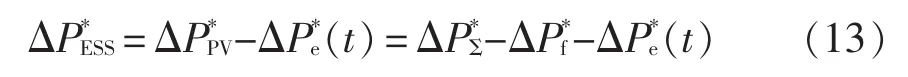
对式(13)求导,则储能系统的功率变化率为

考虑到a1<0恒成立,因而基于式(14),可知功率变化率满足不等式

当且仅当T=0,即没有平滑算法时,等号成立。
为便于分析,将求解功率变化率最大值转化为求解 f(t)最大值。对 f(t)求导,并计算其极值,可得,当有最大值,即

探究平滑算法的影响,实际可以看作探究时间常数T的影响。当T=0时,截止频率fc无穷大,此时并无平滑算法加入;当T≠0时,平滑算法才工作。由此,求解式(15)对时间常数T的偏导数,可得平滑算法对 f(t)|max的影响,即
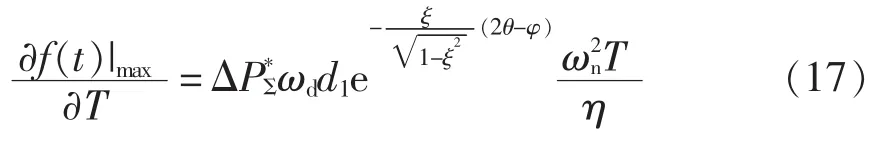
其中,η恒小于0。可知式(17)恒小于0,即随着时间常数 T 的增大,f(t)|max逐渐减小。综合式(15)可以推断:平滑算法确实可以降低储能系统功率变化率的约束条件;且随着时间常数T的增大,储能系统功率变化率大致呈下降趋势。
2.3 平滑算法对储能物理约束的影响
不同类型的储能系统具有不同的功率密度、响应时间以及能量密度[11],因而在设计系统时,需要关注储能单元所需的功率、调节时间以及能量三大指标,即储能物理约束。
对式(13)求导数,并计算其极值,可得:当t=0时,储能单元所需提供功率最大,即
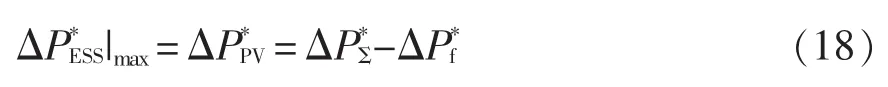
式(18)与时间常数T无关,可以推断:平滑算法的加入并不会影响储能系统的最大功率。
为便于分析,对储能单元调节时间的判断,不妨转化为对系统输出功率调节时间的计算,二者讨论结果一致。由式(11)可以得到系统阶跃响应的两条包络线:,响应曲线总在包络线中变化。当允许误差为5%时,调节时间ts满足公式

式(19)为调节时间ts与滤波器的时间常数T的隐函数,可以通过迭代求解。相比传统二阶系统,平滑算法的加入使得式(19)中引入了时间常数T对应的分量,同样会对调节时间ts产生影响。
为缩短调节时间,设计滤波器时间常数T满足

此时,a1始终小于 0,d1在间变化。对比传统二阶系统,可以推断:当滤波器满足式(20)所对应的条件时,平滑算法不仅可以降低功率变化率,还能加速输出功率稳定,减小系统调节时间ts。
本文选用储能单元总吸收能量表征系统的能量约束。将式(13)对时间进行积分,可得储能系统所吸收的能量对时间的变化关系式为
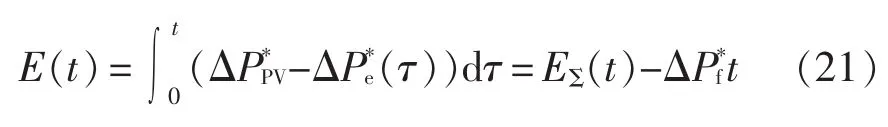
其中,EΣ(t)表征频率调节分量时,储能系统吸收的能量,即
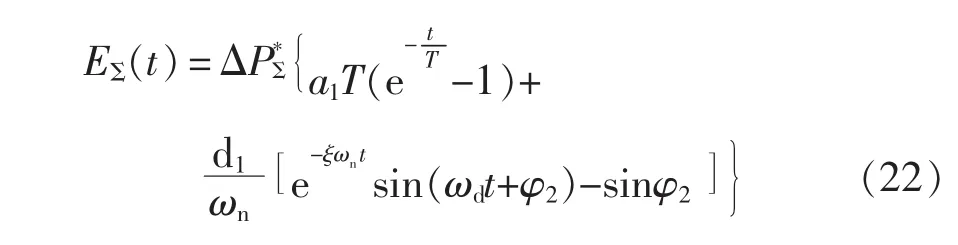
综合式(21)和式(22),可知平滑算法仅与 EΣ(t)分量有关,为简化分析,不妨假定频率调节分量=0,讨论此时平滑算法对储能系统所需能量的影响。
当t→∞时,基于式(22)求得储能系统所需吸收的总能量为
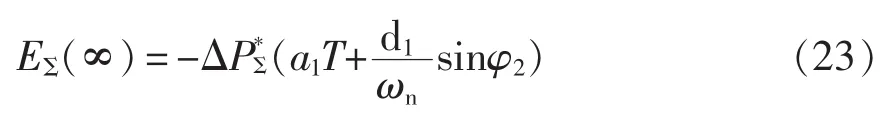
由此,求式(23)对T的偏导数,可得平滑单元对储能容量的影响为

进一步求导可知, 当 T<ξ/ωn时,随T增大而递减;当 T>ξ/ωn时,随T增大而递增。存在最小值,即

式(25)恒大于0。又,当T=0,即没有平滑算法时,储能单元所需吸收的总能量为

可以推断:平滑算法的加入会增大系统对储能容量的需求,且随着T的增加,其需求也会增大。
综上,对于固定的系统参数J、D,平滑算法的加入不会影响储能系统的功率约束,经过合理设计滤波器,可以减小系统的调节时间ts,但会增大系统对储能容量的需求。
3 无功提供能力研究
平滑算法的加入对储能系统的物理约束产生了影响,实际上,系统输出的无功功率同样会影响储能边界[15]。
由第2节可知,平滑算法会影响系统输入阶跃变化时的储能容量EΣ。假定频率调节分量,讨论此时平滑单元对调节范围的影响。
式(23)实质为同步功率SE的隐式,化简可得储能系统吸收能量EΣ(∞)与同步功率SE关系式为
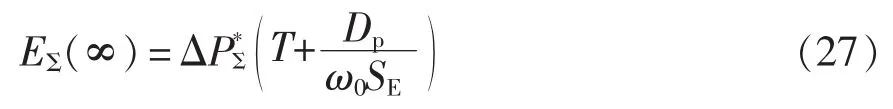
固定EΣ,求解式(27)对T的偏导数,可以得到平滑算法对无功功率参考值的影响

式(28)恒大于0。可以推断:当储能物理约束固定时,平滑算法的加入会减小系统可提供无功功率的范围;随着T的增加,无功功率的取值下限逐渐增大,但并不影响系统的最大无功调节能力。
4 仿真验证
为验证前文讨论的平滑环节对储能系统物理约束以及无功提供能力的影响,本文使用PSCAD软件搭建了一台100 kVA的VSG仿真模型。系统参数与图1对应,见表1。

表1 系统参数Tab.1 System parameters
4.1 VSG基础功能验证
为验证VSG系统的基础功能,设置仿真扰动如下:0 s时,设置系统在0 kW/0 var指令下启动;0.5 s时,改变系统功率指令为10 kW/0 var;1.0 s时,电网电压幅值Um从311 V跌落为300 V;1.5 s时,电网频率f从50 Hz阶跃为50.1 Hz。仿真结果如图5所示。
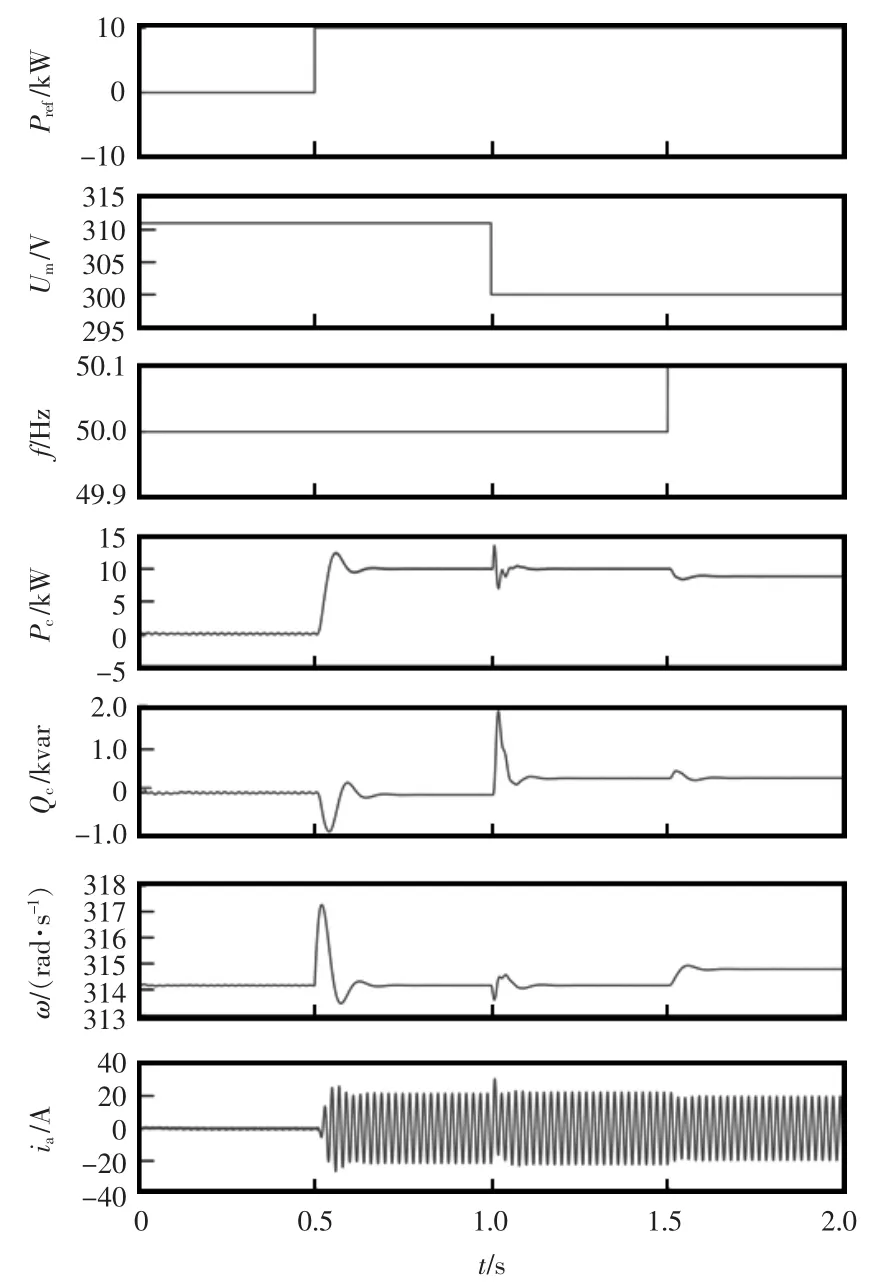
图5 VSG仿真结果Fig.5 Simulation results of VSG
由图5可知,当VSG系统的有功指令、电网电压以及电网频率发生改变时,VSG系统都会相应变化。输出的有功功率与无功功率间存在动态耦合;其外特性表现出与同步机相类似的惯性和阻尼特性;基于下垂控制,虚拟转子角速度可以与电网频率同步运行。
4.2 平滑算法对物理约束的影响
图6中各系统参数所对应的调节时间见表2。综合图6及表2,可以明显看出,平滑算法使得储能系统功率变化率的最大值有所减小。
对于不同的系统参数组,平滑算法对其物理约束的影响相同:储能系统的最大功率恒定,不因平滑算法而发生变化;平滑算法可以明显地增加储能系统的总吸收能量;在所选时间常数下,虽然平滑算法增大了系统响应的上升时间,但可以降低系统输出波动,减小动态调节时间。与前文讨论结果相符合。
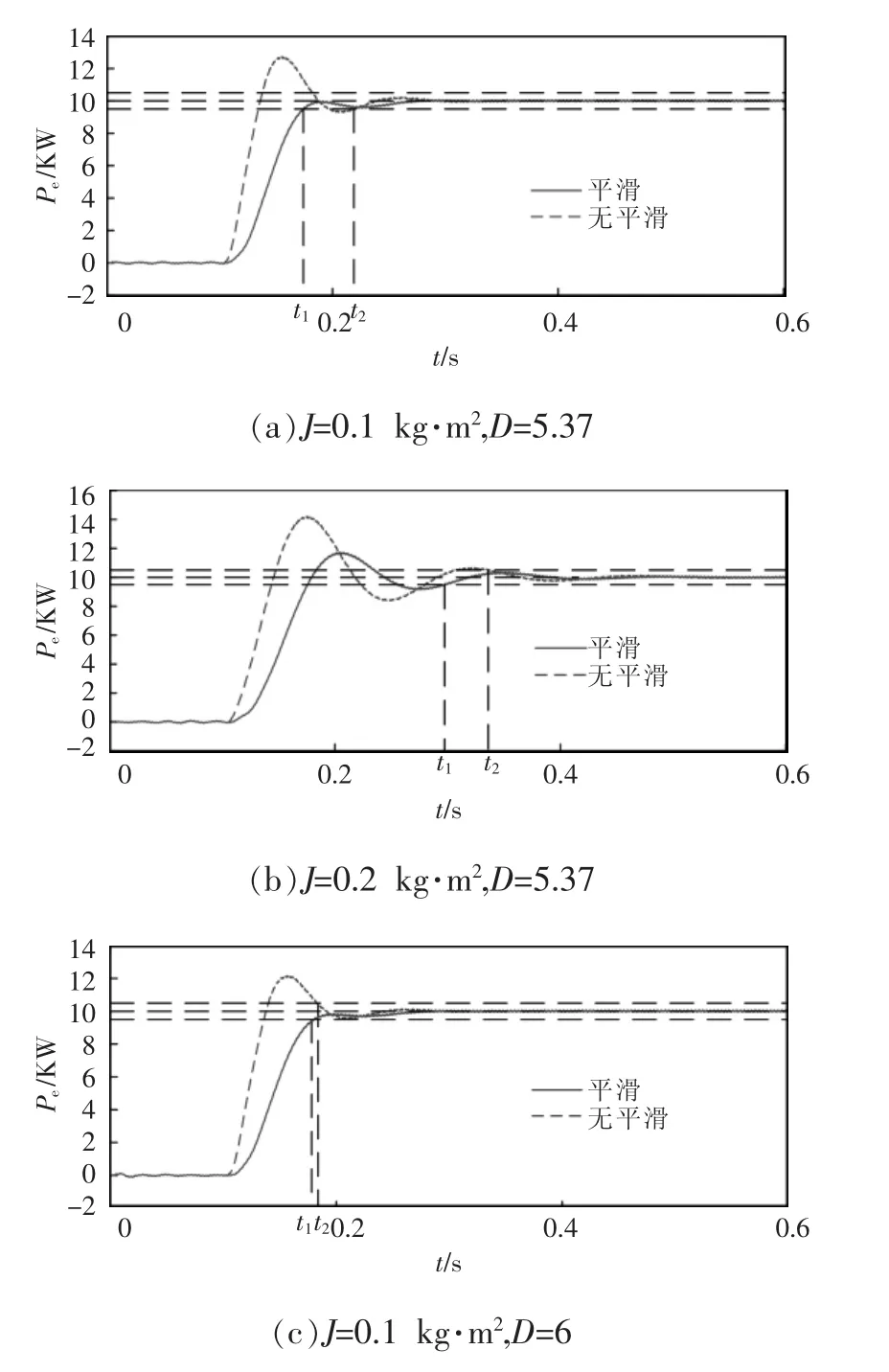
图6 不同惯性和阻尼下系统有功功率响应Fig.6 Responses of active power to different inertia and damping
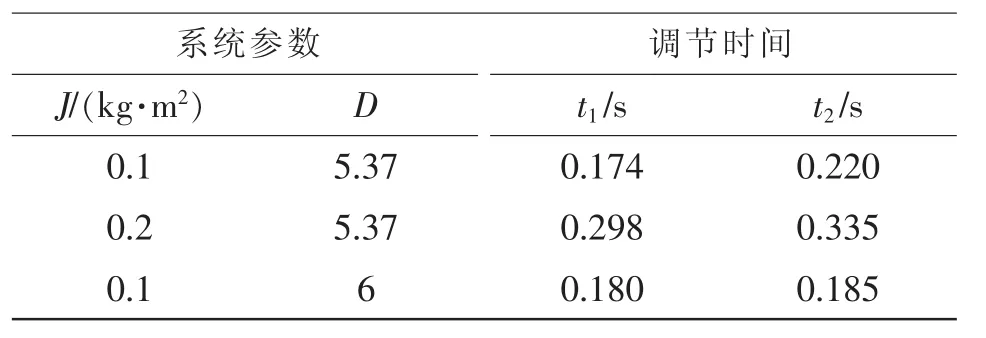
表2 调节时间Tab.2 Setting time
4.3 平滑算法对无功功率提供能力的影响
固定储能容量边界时,平滑算法的加入会提升无功输出最小值,从而缩小无功调节范围。此时设定系统参数恒定:J=0.1 kg·m2,D=7, 改变无功功率指令,可以得到平滑算法对无功调节能力的影响,如图7所示。
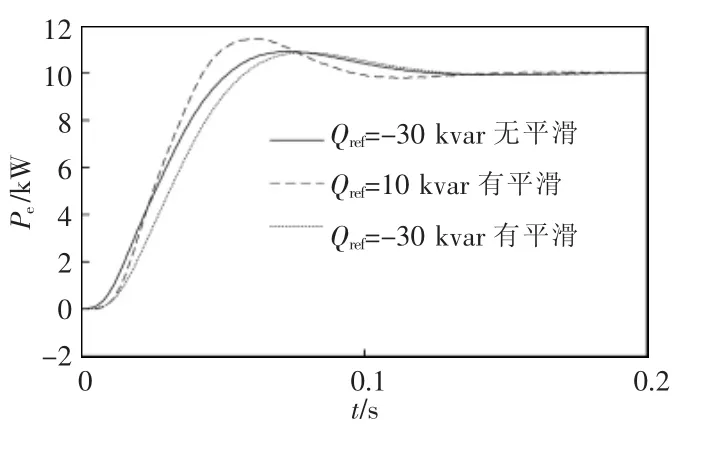
图7 不同无功功率下系统的有功功率响应Fig.7 Responses of active power to different reactive powers
由图7可见,恒定系统参数时,平滑单元的加入会增大系统对储能容量的需求;系统输出的无功功率与储能容量成反比。所以,当限定储能物理约束时,平滑算法对储能容量的增大作用需要通过提高系统的无功输出下限、减小无功调节范围进行补偿。
4.4 平滑算法对系统稳态的影响
使用Matlab/Simulink工具对稳态系统输出电流以及输出功率进行仿真分析。设定系统参数:J=0.1 kg·m2,D=7,通过增加和去除平滑环节,可得平滑算法对a相输出电流谐波的影响,如图8所示。
由图8可见,无论是否加入平滑环节,稳态时电流基频分量(50 Hz)的幅值均为20.78 A,THD均为1.92%;输出电流中存在奇次谐波,但其含量极小,也不会因平滑环节有所变化。
本文还对系统输出功率和频率进行仿真,发现系统有功功率和电压频率最终都会收敛到有功参考值和电网频率,维持稳定运行,与有无平滑算法无关。由此可以验证,系统稳态特性并不会因平滑算法的加入有所变化。
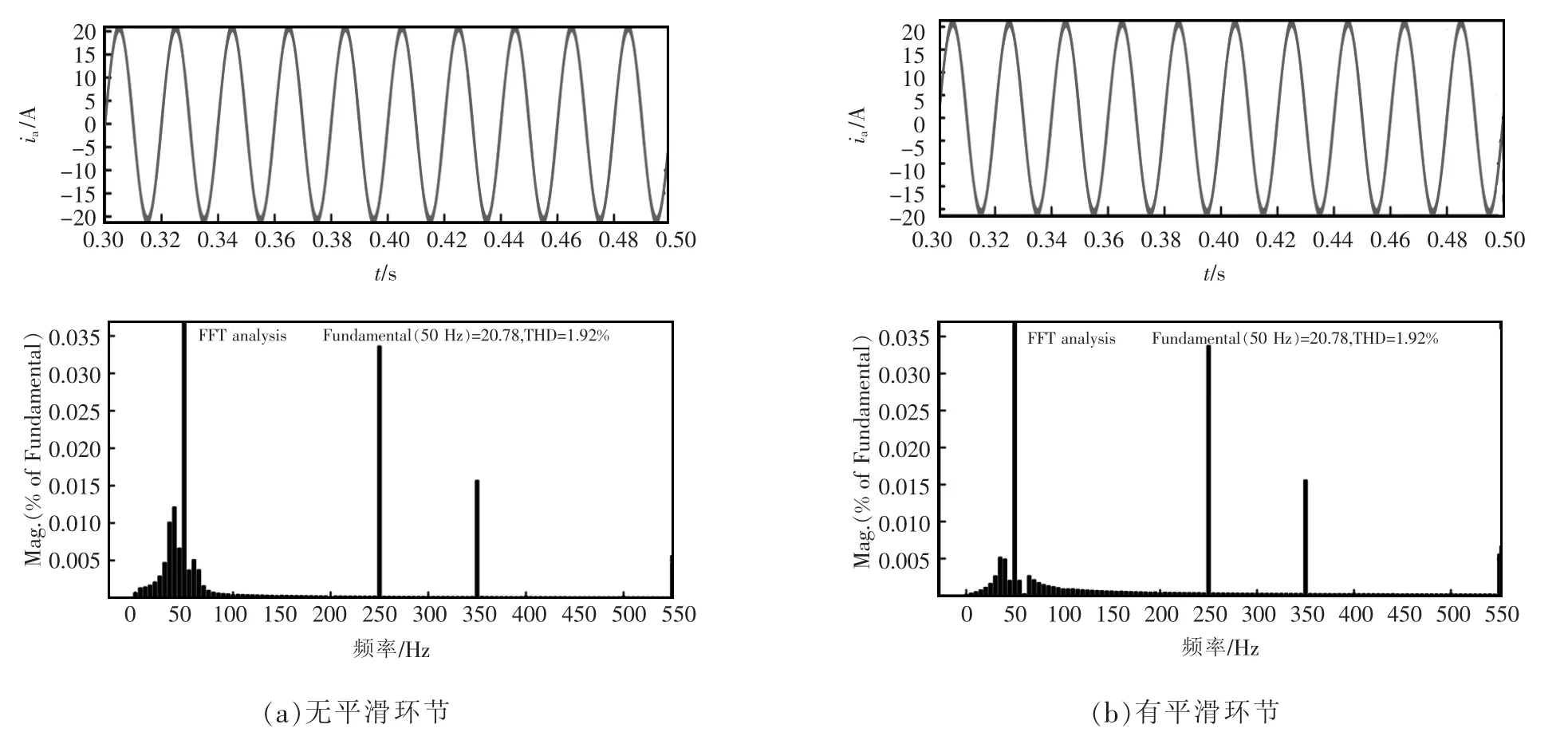
图8 平滑算法对a相电流谐波的影响Fig.8 Influence of smoothing algorithm on a-phase current harmonics
5 结论
由于传统分布式发电机组无法为系统提供阻尼特性和转动惯量,会降低电网稳定性。基于虚拟同步发电机策略,可以使逆变器输出特性模拟同步机,对电网的等效惯量和阻尼进行补偿。光伏出力与电网负荷存在波动,为降低其对储能系统造成频繁充放电的不利影响,可以采用平滑算法进行抑制。平滑算法的实现同样依靠储能系统提供物理基础,因而也会对虚拟同步机的运行特性,尤其是对物理约束产生影响。对VSG平滑算法的研究,有助于明确VSG的物理运行边界。本文针对VSG控制模型、平滑算法、储能系统的物理边界以及系统提供无功功率的能力进行了研究,结论如下。
(1)基于储能系统的备用能量以及VSG控制策略,可以将并网逆变器输出特性虚拟为同步发电机,表现出惯性和阻尼特性。
(2)平滑算法不会影响储能系统的功率边界;当滤波器满足式(20)所对应的条件时,平滑算法不仅可以降低功率变化率,还能加速输出功率稳定,减小系统调节时间;但是平滑单元的加入也会增大系统对储能容量的需求,并且随着时间常数的增加,其需求也会增大。
(3)平滑算法也会对系统的无功功率提供能力产生影响。当物理约束限定时,平滑环节会提高系统无功输出的下限,限制系统输出无功功率的调节范围。

