边界条件对相干光位相恢复的影响研究

赵致远，景文博，邹欢欢

（1.长春理工大学 光电工程学院，长春 130022；2.长春理工大学 电子信息工程学院，长春 130022）

在相干光条件下，复振幅是光场的空间分布。它包括光强和位相，能够完整的描述光场信息。光学成像仪器CCD能够采集到光场的强度信息，但是无法记录位相信息。如何通过采集到的强度信息来计算出光场的位相信息，是现代光学中要解决的重要问题。常用的位相恢复方法包括干涉测量方法、Pyramid传感、Hartman传感、强度传输方程（TIE）法和相干衍射成像方法（CDI）法等。干涉测量方法原理是使待测光束和一束参考光进行干涉，以干涉条纹的形式记录位相信息[1]。该方法测量精度高，但引入了参考光使得光路结构复杂，并且对环境要求苛刻。Pyramid传感器及Shark-Hartman传感器的特点是光路简单并且可测量非相干光的波前，工程化程度高，实时性好，但其测量精度受到微透镜阵列的结构限制[2,3]。TIE法也可以测量非相干光的波前，但是测量系统中需要添加透镜，因此在X射线等领域应用受限[4]。CDI技术是一种利用卷积理论和衍射定理，通过菲涅耳衍射面上记录一幅或多幅光强信息，结合迭代运算恢复位相信息的方法[5,6]。该方法的光路简单，恢复精度不受光学元件质量限制，且在X射线等领域应用广泛。本文采用CDI成像系统，采集两个面的强度图像且已知两个面的距离，通过迭代变换算法完成对相干光的位相恢复。其中，两个边界条件对恢复精度的影响程度，是本文主要研究的问题。

1 基本原理

相干光无透镜成像系统如图1所示。相干光束由相干光出射面射出，传播距离z后到达U1面，记录U1面的强度I1。相干光束继续传播距离d后到达U2面，记录U2面的强度I2。通过I1，I2，d及迭代变换算法，恢复相干光位相信息。

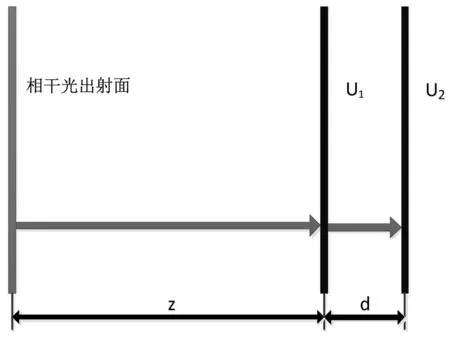
图1 相干光无透镜成像系统

迭代变换算法流程如图2所示。迭代的初始复振幅g可用I1和一个随机位相分布θ0表示：

经过k次迭代，U2面的复振幅可由gk(x)经过角谱传播后得到：

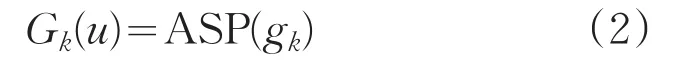
ASP代表角谱传播：

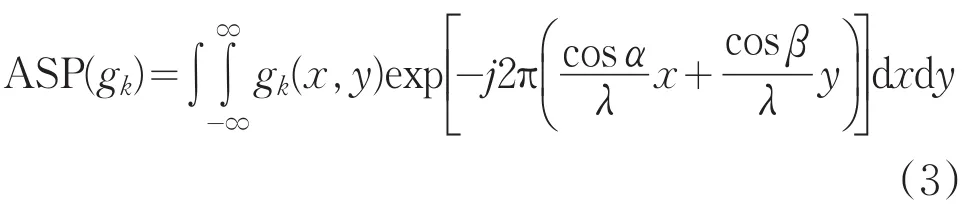
在保持位相不变的条件下，将传播后的强度信息替换成I2结合之后提到的外推法边界条件得到：

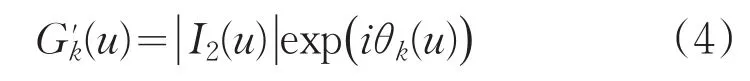
式（4）中的θk(u)是k次迭代的位相估计。然后对替换强度后的复振幅进行逆角谱传播，结合之后提到的混合输入输出法（HIO）边界条件来形成新的gk+1(x)：

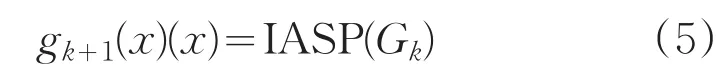
IASP代表逆角谱传播。该算法遍历这个循环，直到找到满足两个约束条件的输出，或者算法停滞不前，没有进一步的进展时结束。这些算法的收敛性通常是由约束误差来控制的：

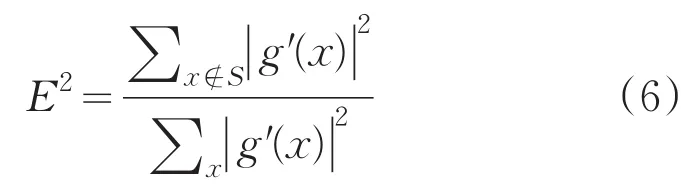
式中S表示U1面强度图像中光斑的区域，在这种条件下算法收敛。

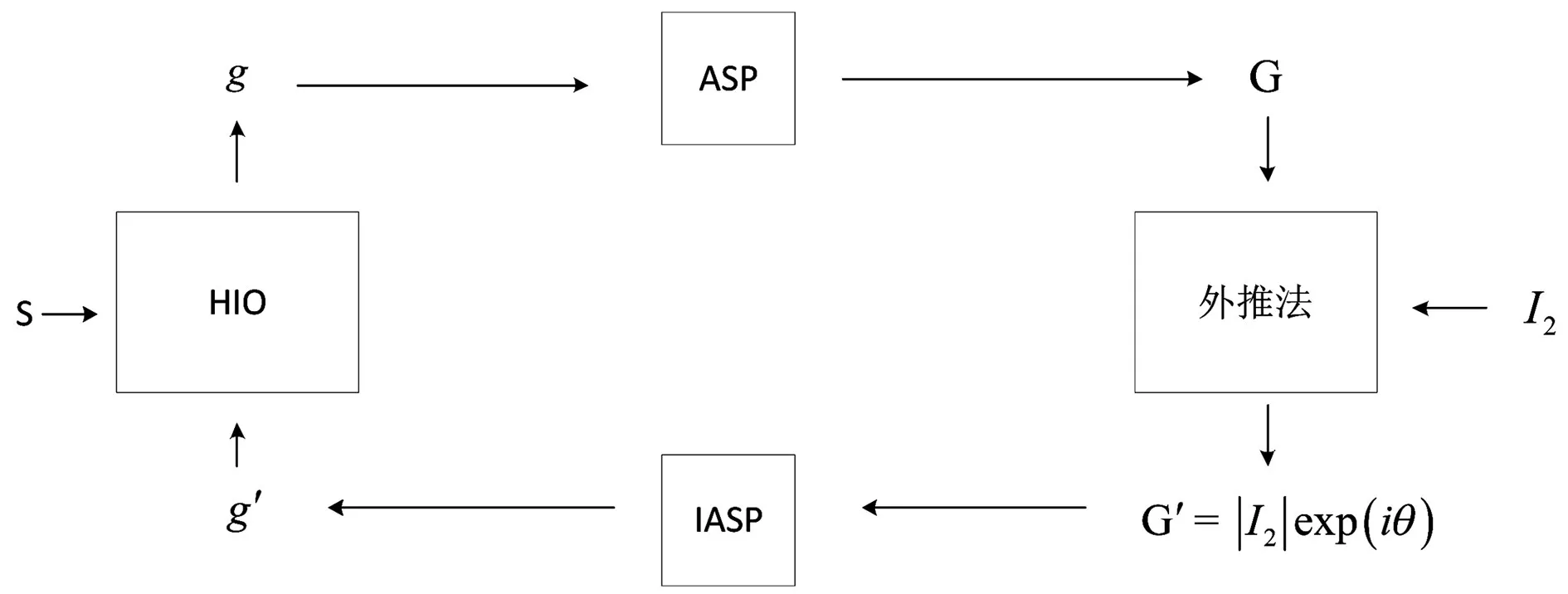
图2 迭代变换算法

2 边界条件

2.1 HIO边界条件

由于CCD相机固有的属性，在实际采集相干光强度信息时难免会有噪声的影响。通过一般的滤波处理比如：

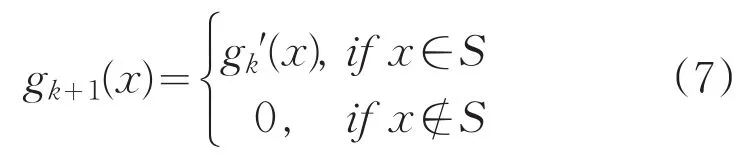
虽然迭代可以收敛，但是要避开局部极小值是不可能的，并且使得算法容易陷入停滞。

HIO边界条件又称为混合输入输出法。在有效区域以外的地方，该算法使用之前的输入来驱动输出：

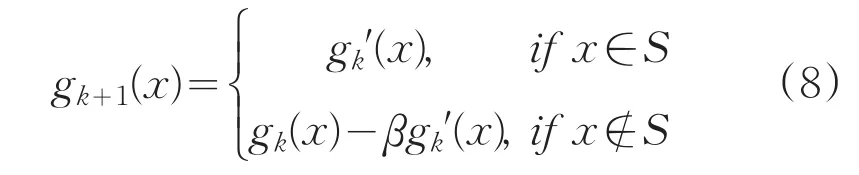
反馈参数β通常在0：5和0：8之间分配一个值。已经证明HIO边界条件能够成功地避开局部最小值，是重建复杂图像的重要工具。

好的结果通常是通过结合使用迭代变换算法和HIO边界条件来获得的，在大多数迭代中使用HIO边界条件来探索解空间，并周期性地执行几次误差减少的迭代，以帮助当前的重建稳定下来。虽然这种算法组合已被证明是正确的，但它仍然可能被困在非常持久的停滞模式中，尤其是应用于以最简单形式的复值图像重建。

2.2 外推法边界条件

在现实世界中，由于光学系统的有限孔径，即使感兴趣的对象有一个硬边界支持，它的图像都将会有旁瓣出现。在傅里叶空间中，为了绕过旁瓣问题，提出了一种基于加权投影的可控外推技术。外推法边界条件又称为外推法[7]。加权投影是通过代替傅里叶变换实现的：

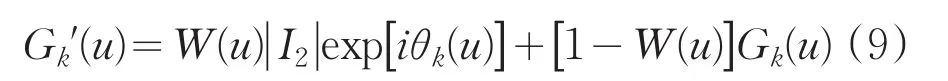
其中W(u)是权重函数：

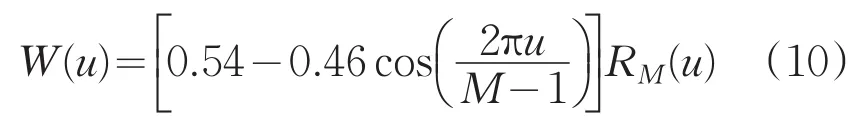
当W(u)=1时，傅立叶幅度约束被执行；当W(u)=0时，Gk(u)的幅度和位相保持不变；当0＜W(u)＜1时，Gk(u)介于两种情况之间。公式（1）表示对傅里叶幅度约束的宽松投影。一般而言，数据外推的问题比插值的稳定性差，并且随着离测量数据越远，计算的外推就越不确定。因此，使用的权重函数不允许外推在整个计算窗口中自由扩展。在测量窗口之外使用非二进制加权函数可以使算法稍微外推测量数据。目的是为了使傅立叶数据外推足以使其与硬边对象支持约束一致。这有效地扩展了解决方案的空间，从而包含了衍射限制条件，不需要引入大量的自由参数。

对于本文中的外推技术，HIO的作用是将测量数据嵌入到更大的零点阵列中。加权函数W(u)，如图3所示。图3在测量区域内设置为1，以便测量的强度得到执行。在零填充区域中，权重在测量幅度的边缘处从零开始，并在计算窗口的边缘处逐渐增加到1。该加权函数允许算法在接近测量数据时自由扩展，并在接近计算窗口边缘时逐渐减少零幅度，从而允许分析更多测量数据，同时防止缠绕效应。

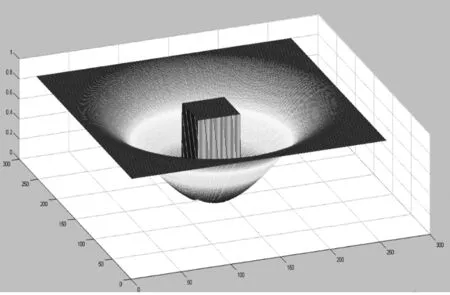
图3 权重函数示意图

3 实验研究

3.1 实验系统描述

为了验证相干光无透镜成像系统对相干光位相恢复的可行性，以相干光源为例搭建相应的实验系统，研究了光照充足条件下该系统对静态像差的探测能力，实验系统光路图与实物照片分别如图4和图5所示。实验系统由氦氖激光器，激光衰减组，CCD相机组成。氦氖激光器输出的光束经过激光衰减组，以保证激光光强在一个合理的阈值。光束在CCD相机上成像并记录，之后沿光路方向移动CCD相机使光束再次在CCD相机上成像并记录。

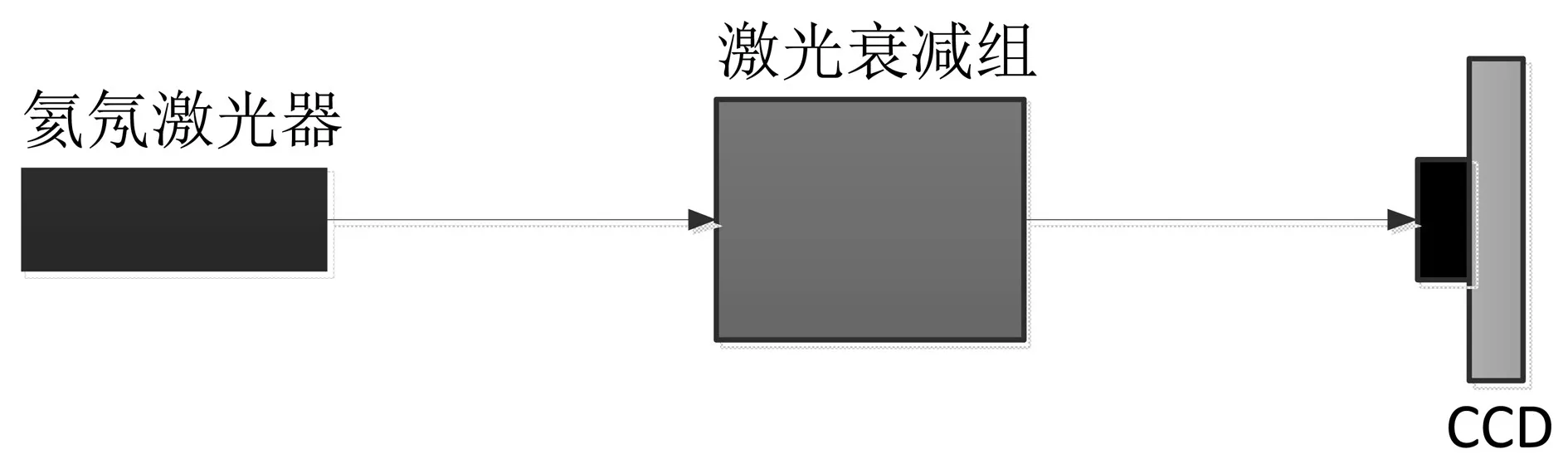
图4 实验系统光路图

图5 实物照片

3.2 实验结果

根据上述的两种边界条件对迭代变换算法进行改造，形成了新的迭代变换算法。它们分别是只使用HIO边界条件的迭代变换算法和只使用外推法的迭代变换算法，以及两种边界条件相结合的迭代变换算法。利用上述的实验系统中两台CCD采集到的光斑强度图像如图6（a）和图6（b）所示，两台CCD的轴向距离d=5mm。通过上述两幅强度图像及传播距离实验研究三种迭代变换算法对相干光位相恢复的效果并与干涉检验方法进行对比。干涉检验方法得到的位相结果如图6（c）所示。

为了研究HIO边界条件对位相恢复的效果，将公式（9）改写为：

不经过外推法边界条件限制的位相恢复的效果如图6（d）所示，其残差如图7（a）所示；为了研究外推法边界条件对位相恢复的效果，原先HIO边界条件采用公式（7）。其位相恢复的效果如图6（e）所示，其残差如图7（b）所示；两边界条件共同作用的位相恢复效果如图6（f）所示，其残差如图7（c）所示。

图6 光斑强度图像

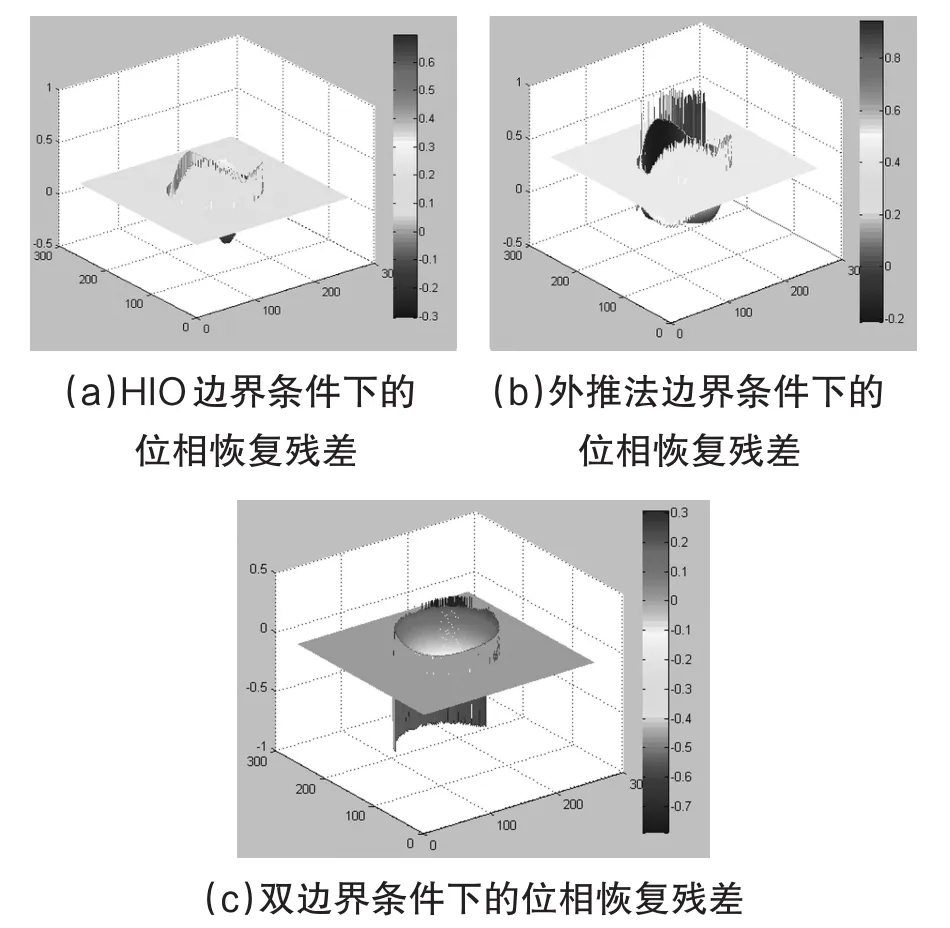
图7 残差图像

位相恢复效果的约束误差由公式（6）表示。HIO边界条件的约束误差如图8（a）所示，其RMS=0.0189λ；外推法边界条件的约束误差如图8（b）所示，其RMS=0.0096λ；双边界条件的约束误差如图8（c）所示，其RMS=0.0012λ；结果表明双边界条件的限制能有效提高位相的恢复精度。

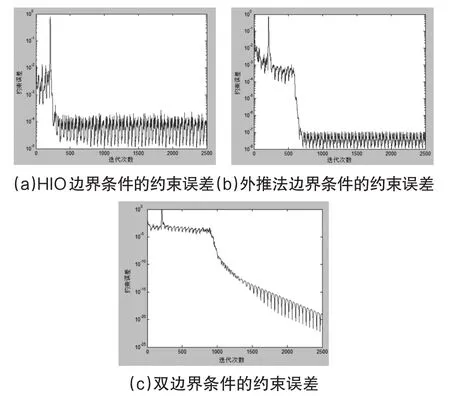
图8 约束误差图像

4 结论

本文基于相干光无透镜成像系统，设计了一套双边界条件位相恢复方法。该方法有三个特点：（1）该位相恢复方法由于没有使用透镜，没有引入多余的系统误差，且有较广的波长适用范围；（2）该系统搭建光路简单，对外界环境要求较低；（3）由于双边界的限制，该位相恢复系统中的迭代算法鲁棒性强，不易停滞且有效限制了傅里叶空间中的旁瓣问题。本文对双边界条件进行了误差分析，结果表明双边界条件的限制能有效提高位相的恢复精度。