考虑预防和保护的项目风险应对预算分配方法
,
(东北大学 工商管理学院,辽宁 沈阳 110167)
1 引言
在项目实施过程中,项目风险是客观存在的,其一旦发生往往会对项目造成不利影响,严重者可导致项目失败[1,2]。因此,为了保证项目顺利完成,采取有效的应对策略来减缓风险显得至关重要[3]。应对策略的实施往往需要资金上的支持。针对某一策略,较高的预算投入通常能带来较好的应对效果,同时也将导致较高的项目成本,那么,在进行风险应对时,如何权衡策略的应对效果以及其实施成本,并在此基础上进行风险应对预算的合理分配是一个具有现实意义的研究问题。
目前,关于项目风险应对的研究多数将关注焦点放在项目风险应对策略选择问题上,并提出了一些方法来确定风险应对策略集合,如基于权衡的方法[4~10],基于决策树的方法[11~15],基于相似案例的方法[16~18],以及基于优化的方法[3,19~27]等。然而,关于项目风险应对预算分配问题的研究还比较缺乏[27,28]。Sherali等[28]采用事件树来分析风险发生后各种结果事件的逻辑顺序及发生概率,在此基础上构建优化模型来进行风险减缓资源的最优分配。Sato和Hirao[29]针对项目预算和项目关键风险之间的权衡问题,以最大化基于风险的项目价值为目标构建优化模型来进行项目各工作活动之间的预算分配。可以看出,文献[28]中风险减缓资源分配的目的是减少风险发生后的损失,而文献[29]是为了降低项目活动中风险发生的概率。实际项目风险管理中,项目经理通常会从降低风险概率和减少风险损失两个方面来应对风险。如工业生产项目中,设置安全警示牌来减少安全风险的发生概率,设置点火喷水装置来降低安全风险所带来的损失。同时,一些研究也指出了项目风险应对需要从风险预防和风险保护两个方面进行,并将风险应对策略分为风险预防策略和风险保护策略[3,23]。其中风险预防策略指的是通过降低风险发生概率来应对风险的措施,通常在计划阶段执行;风险保护策略指的是通过减少风险损失来应对风险的措施,通常在风险发生后实施[3,27]。但是,这些研究仅给出了最优风险应对策略的选择方法[27],并未涉及如何在预防策略和保护策略之间进行应对预算的合理分配。
可以看出,上述文献虽然对项目风险应对的相关研究做出了许多贡献,但是仍然存在着以下不足:以往研究很少关注风险应对预算分配问题,使得其对项目管理实践的指导较为有限;已有研究大多假设策略的实施效果及成本是固定的。实际中,策略的效果往往与策略本身、风险特性以及所投入的预算有关。比如,实施预防策略或保护策略都能在一定程度上降低风险,然而对两种策略投入相同的预算所带来的风险降低程度可能不同;同时当初始风险特性不同时,针对同一策略投入相同的预算所带来的应对效果也会有所不同。当初始风险概率或损失较大时,实施应对策略通常能显著地降低风险;而当风险较小时,若想获得相同的风险降低程度往往需要投入更多的预算。针对现有研究的不足,本文尝试对策略的效果与策略本身、风险特性以及所投入预算之间的关系进行分析,并在此基础上探讨项目风险应对预算分配问题。首先,分析风险预防策略或保护策略的效果与策略本身、风险特性以及所投入预算之间的关系,并给出相应的关系表达式;其次,在满足风险控制要求的约束下,以最小化风险应对预算为目标构建考虑预防和保护的风险应对预算分配优化模型,通过模型求解,可得到最优的应对预算分配决策。最后,通过分析最优决策得到一些有价值的定理和结论,从而为项目风险应对的相关决策提供支持与参考。
2 风险应对策略分析
本节对策略效果与策略本身、风险特性以及预算之间的关系进行分析。本文涉及到的变量符号及相应说明见表1。

表1 变量符号及其说明
2.1 风险预防策略
风险预防的目的是尽可能地降低风险概率,进而减少风险期望损失[3]。那么,预防策略的效果体现在能将风险概率降低到何种程度。以往研究认为风险概率与应对预算之间的关系呈现向下凸的曲线形式[3,29]。即,当向预防策略不投入预算时,风险发生概率保持不变,与初始风险概率相同;随着所投入预算的增加,风险概率呈现降低的趋势。通常情形下,当风险概率已处于较低水平时,随着预算的持续投入,风险概率降低的程度会越来越小。此外,在不更改项目活动的情况下,任何策略都不能保证项目免受风险,那么无论向预防策略投入多少预算,风险概率只能无限接近于一个相对较低的值。基于上述分析,风险概率和所投入预算之间的关系应满足如下性质:(1)当q=0时,P=P0;(2)∂P/∂q<0,∂2P/∂q2>0;(3)当q→∞时,P→ε。
综上,给出风险预防预算与风险概率的关系式,如(1)式所示
P=(aεq+P0)/(aq+1)
(1)
其中a为风险预防系数,表示单位预算投入所带来的风险概率的降低程度,a越大,P越小。
2.2 风险保护策略
风险保护策略的效果体现在能将风险损失降低到何种程度。类似地,风险损失与所投入预算之间的关系应满足如下性质:(1)当r=0时,L=L0;(2)∂L/∂r<0,∂2L/∂r2>0;(3)当r→∞时,L→δ。
与风险预防预算和风险概率的关系式相似,风险保护预算与风险损失之间的关系表达式为
L=(bδr+L0)/(br+1)
(2)
其中b为风险保护系数,表示单位预算投入所带来的风险损失的降低程度,b越大,L越小。
为了避免由于风险概率和风险损失取值范围不同对风险应对预算分配决策所产生的影响,将初始风险损失的取值进行归一化处理,使得L0∈[0,1]。
3 项目风险应对预算分配优化模型
3.1 问题描述
考虑项目面临一个关键风险,项目风险管理小组对该风险进行了分析和评估,得到该风险的发生概率P0以及风险发生之后所带来的损失L0。为了将该风险降低在项目可接受水平内,项目风险管理小组提出了一个预防策略和一个保护策略,分别用来减少风险概率和风险损失。预防策略或保护策略的效果与对其投入的预算有关。那么本文要解决的问题是,在满足项目风险控制要求的前提下,如何在预防策略和保护策略之间进行预算分配,使得所投入的总风险应对预算最小。
依据上述分析,以风险应对预算最小为目标,以满足风险控制要求为约束构建优化模型,如下
minC=q+r
(3)
s.t.PL=R
(4)
q≥0,r≥0
(5)
其中q、r为决策变量;(4)式是风险控制要求约束,R为可接受的风险期望损失,即项目风险控制要求,可由项目经理确定。这里假设R>εδ,因为R≤εδ意味着无论投入多少努力都不可能满足风险控制要求,那么风险应对决策将变得毫无意义。
3.2 结果分析
对模型进行求解分析,可得到以下定理和结论。
定理1优化模型(3)~(5)的最优解存在且唯一,即
(6)
(7)
最优的风险应对预算为
(8)
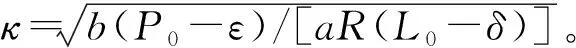
证明由于预防预算和风险概率、保护预算和风险损失之间是一对一的关系,那么求解最优的风险概率和风险损失,就能得到预防预算和保护预算的最优解。
对(1)式和(2)式进行变换,可得到预防预算关于风险概率的表达式q=(P0-P)/[a(P-ε)],保护预算关于风险损失的表达式r=(L0-L)/[b(L-δ)];由(4)式可知L=R/P,将上述表达式代入(3)式,可得到风险应对预算关于风险概率的表达式如下
(9)
对(9)式分别求风险应对预算关于P的一阶导数和二阶导数可得
(10)
(11)
显然∂2C/∂P2>0,即风险应对预算是关于P的严格凸函数,最优解存在且唯一。因此,由一阶条件∂C/∂P=0可得到最优的风险概率,相应地,将最优风险概率代入(1)~(4)式,可得到最优的预防预算、保护预算以及风险应对预算。证毕。
对定理1进行分析可得到如下结论。
结论1风险控制要求对风险应对预算分配决策的影响如下
∂q*/∂R<0,∂r*/∂R<0,∂C*/∂R<0
证明分别求q*和r*关于风险控制要求R的一阶导数,可得
由于P0>ε,L0>δ,R>εδ,那么,∂q*/∂R<0,∂r*/∂R<0,进而∂C*/∂R<0。证毕。
结论1表明,最优的预防预算q*、最优的保护预算r*以及总风险应对预算C*都与可接受的风险期望损失R负相关。较高的R意味着项目经理对风险控制的要求较低,即将风险控制在较高的风险期望损失内就能使项目经理满意,此时,对风险预防和风险保护投入的预算也较低;而当项目经理对风险控制要求越来越严格时,需要同时增加对风险预防和风险保护投入的预算,相应地,总的风险应对预算也随之增加。
结论2初始风险概率对风险应对预算分配决策的影响如下
∂q*/∂P0>∂r*/∂P0>0, ∂C*/∂P0>0
证明分别求q*和r*关于初始风险概率P0的一阶导数,可得∂q*/∂P0=(1/2+κδ)/[aκ(R-εδ)],∂r*/∂P0=κR(L0-δ)/[2b(P0-ε)(R-εδ)],那么,∂q*/∂P0-∂r*/∂P0=δ/[a(R-εδ)]>0;显然,∂q*/∂P0>∂r*/∂P0>0,进而∂C*/∂P0>0。证毕。
结论2表明,随着初始风险概率P0的增加,最优的风险预防预算q*、风险保护预算r*以及总风险应对预算C*呈现递增的趋势,且最优预防预算q*的增加速度大于最优保护预算r*的增加速度。即当初始风险概率增加时,若想满足项目风险控制要求,不仅需要追加预防预算,同时还需追加保护预算。这是因为,在同样的风险控制要求下,减少较高的初始风险概率需要投入较高的风险预防预算,而当将风险概率降低到一定程度后,单位预防预算所带来的概率降低程度较小,此时可以通过增加风险保护预算的方式来降低风险损失,进而达到降低风险期望损失的目的。
结论3初始风险损失对风险应对预算分配决策的影响如下
∂r*/∂L0>∂q*/∂L0>0, ∂C*/∂L0>0
证明求q*和r*对初始损失L0的一阶导数,可得∂q*/∂L0=(P0-ε)/[2aκ(L0-δ)(R-εδ)]、∂r*/∂L0=(κR+2ε)/[2b(R-εδ)],∂r*/∂L0-∂q*/∂L0=ε/[b(R-εδ)]>0,显然,∂r*/∂L0>∂q*/∂L0>0,∂C*/∂L0>0。证毕。
结论3表明,随着初始风险损失L0的增加,最优预防预算q*、保护预算r*以及风险应对预算C*均呈现增加趋势,且保护预算r*的增加速度高于预防预算q*的增加速度。这是由于初始风险损失的增加使得初始风险期望损失增加,若要满足相同的风险控制要求,则需要向预防策略和保护策略投入更多的预算来降低风险。同时,单位预算所带来的应对效果与风险概率或损失的初始值有关,当初始损失(或概率)较大时,预算投入到风险保护(或预防)所得到应对效果较好。因此,随着初始风险损失的增加,风险预防预算和保护预算都会增加,且风险保护预算的增加速度较快。
定理2最优的风险预防预算q*和风险保护预算r*之间的关系如表2所示。

表2 最优的预防预算和保护预算之间的关系
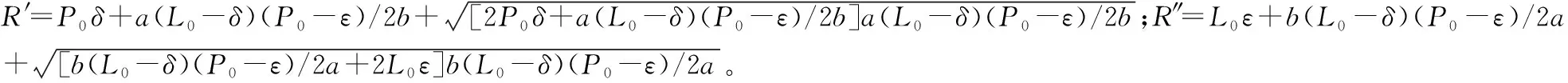
证明首先,证明最优风险预防预算q*和风险保护预算r*之间的大小关系。比较q*和r*可得
(12)
当P0δ>R且L0ε>R(或P0δ 当P0δ>R且L0ε 其次,证明是否需要同时向风险预防和风险保护投入预算。 当P0δ>R时,意味着单独进行风险保护难以满足项目风险控制要求,因此,需要向风险预防策略投入预算,即q*>0;类似地,当L0ε>R时,表明单独进行风险预防无法将风险期望损失降低到可接受水平,此时需要通过风险保护来降低风险损失,进而达到降低风险期望损失的目的,即r*>0。显然,当P0δ>R且L0ε>R时,需要同时对风险预防策略和风险保护策略投入预算,即q*>0,r*>0;当P0δ 情形1是否存在q*=0以及存在q*=0的条件。 q*=0意味着仅向风险保护投入预算就可以将风险期望损失降低到可接受水平,因此我们在P0δ 若q*=0,意味着最优的风险概率与初始风险概率相同,即P*=P0。由定理1可知,P*=(κR+ε)/(1+κδ),那么P*=P0可替换为(κR+ε)/(1+κδ)=P0。通过公式变换可得 R=P0δ+a(L0-δ)(P0-ε)/2b± (13) R=P0δ+a(L0-δ)(P0-ε)/2b+ 记为R′。即当R=R′时,q*=0。 情形2是否存在r*=0以及存在r*=0的条件。 与情形1相似,r*=0的前提条件是L0ε R=L0ε+b(L0-δ)(P0-ε)/2a+ 记为R″。即存在r*=0的情形,其存在的条件为R=R″。证毕。 对定理2进行分析可得到如下结论。 结论4当单独向风险预防或风险保护投入无限多预算都不能达到风险控制要求时,风险预防和风险保护需要同时投入预算,且有效性较高的策略所投入的预算较多。 证明由定理2可知,在同时进行风险预防和风险保护时,更重视风险预防还是风险保护取决于(P0δ-R)/a和(L0ε-R)/b之间的大小关系。其中P0δ-R表示将损失减少到最低程度时的期望损失与风险控制要求之间的差距,可理解为风险概率的可控程度,当风险概率的可控程度较大时,需要更加关注风险预防,以达到降低风险的目的;a为风险预防系数,a越小表明单位预算能够减少的风险概率越少,此时,更加需要向风险预防投入较多的预算来减少风险概率,从而降低风险期望损失。这里,将(P0δ-R)/a认为是风险预防策略的有效性,类似地,将(L0ε-R)/b认为是风险保护策略的有效性。因而,在满足风险控制要求的条件下,对有效性较高的策略投入更多的预算能使得总风险应对预算最小。证毕。 结论5当仅采取预防策略就能够满足风险控制要求而仅实施保护策略难以满足风险控制要求时,最优风险预防预算大于最优风险保护预算,反之亦然。 结论6存在仅采取单一应对策略就能达到风险控制要求的情形;且在ε=δ=0情形下,当a/b=R/(P0L0)时,仅采取保护策略,最优保护预算为r*=(b-a)/(ab);当a/b=P0L0/R时,仅采取预防策略,最优预防预算为q*=(a-b)/(ab)。 证明由定理2可知,存在仅进行风险预防或风险保护就能满足风险控制要求的情形;当ε=δ=0时,最优风险预防预算和风险保护预算分别为q*=(P0-κR)/(aκR)和r*=(κL0-1)/b。令q*=0可得,a/b=R/(P0L0)且r*=(b-a)/(ab);令r*=0可得,a/b=P0L0/R且q*=(a-b)/(ab)。证毕。 结论6表明,当采取风险应对策略能使风险概率和损失降低到接近零,且预防系数和保护系数的比例与可接受的风险期望损失和初始风险期望损失的比例相等时,仅需向预防系数或保护系数较高的策略投入预算,且所投入的预算与初始风险概率、初始风险损失无关,仅与预防系数和保护系数有关。 本文给出了考虑预防和保护的项目风险应对预算分配方法,通过该方法可得到最优的项目风险应对预算分配决策。对最优决策进行分析,可为项目经理提供如下管理启示及决策建议: (1)项目经理可根据具体的项目、风险以及策略信息来确定风险应对效果与预算之间的关系参数,并依据本文提出的模型确定最优的风险预防预算以及风险保护预算,从而实现以最少的风险应对预算满足项目风险控制要求的目的。最优的项目风险应对预算与项目经理所设定的风险控制要求有关。当项目经理对风险控制的要求较高时,需要向风险预防和风险保护投入较多的预算;当项目经理对风险控制要求较低时,仅需投入较少的风险预防预算和风险保护预算。可以看出,风险控制要求与风险应对预算是两个相互对立的目标,较严格的项目风险控制要求通常会导致较高的风险应对预算投入。因此,项目经理在进行风险应对时,需要在风险控制要求和风险应对预算之间进行权衡。 (2)随着项目的持续开展,风险概率或损失的评估结果将会发生变化,此时需要项目经理及时调整风险应对预算分配决策,以满足项目风险控制要求。具体地,当初始风险概率增加时,项目需要同时增加对预防策略和保护策略的预算投入,且向预防策略增加的预算投入大于向保护策略增加的预算投入;反之亦然。 (3)在实际项目风险管理中,针对多数项目风险,项目经理需要同时实施预防策略和保护策略来降低风险。此时,向预防策略投入更多的预算还是向保护策略投入更多的预算与策略的有效性有关。当初始风险概率较高、风险损失能降低到的最低程度较大且风险预防系数较小时,向风险保护策略投入更多预算已无法满足风险控制要求,此时对风险预防给予更多的关注并加大对风险预防策略的预算投入可以带来更大程度的风险降低,进而能以较少的应对预算来满足风险控制要求。因此,在此种情形下,建议项目经理对风险预防给予更多的关注以及预算投入。反之,当初始风险损失较大、预防后的风险概率下界较大且风险保护系数较小时,建议项目经理更多地关注风险保护并向风险保护策略投入更多的预算。 本文从预防和保护的角度提出了项目风险应对预算分配方法,弥补了已有研究中较少关注应对资源分配问题的不足,丰富了项目风险应对的相关研究内容。本文的研究结论可为项目经理提供风险应对决策支持,具有实际应用价值。未来研究可以考虑采用历史数据拟合的方式给出风险应对预算与应对效果之间的函数关系,从而给出更加准确的描述;此外,后续研究还可以探讨多个风险情形下的应对预算分配问题,以更好地服务于项目风险管理实践。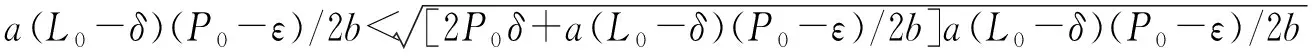
4 结论与启示

