一类非线性Burgers方程组差分格式的计算稳定性*

马永柳，曹艳华

(华北电力大学数理学院，北京 102206)

在利用数值方法求解非线性偏微分方程时会产生计算不稳定性.计算不稳定性不同于线性不稳定性，它是一种突变型的指数增长，且不会随着时间步长和空间步长的改变而改变，因此在求解非线性偏微分方程时首先要分析其计算稳定性.非线性偏微分方程初值问题的解，一般情况下只在时间T的局部范围内存在，即使初值充分光滑，其解的整体存在性也无法确定.相应的解在有限时间内会失去正则性并产生奇解，称为解的破裂[1-2].1968年，C W Hirt[3]提出了分析非线性偏微分方程差分格式计算稳定性的方法，即启发性分析方法.杨晓忠等[4]将启发性分析方法用于判定KdV方程和Burgers方程的差分格式的计算稳定性，并讨论了三时间层和二时间层差分格式的计算稳定性问题，得到了计算稳定性的判断依据.Burgers方程是模拟冲击波传播和反射的非线性数学物理方程，被广泛应用在流体力学、非线性声学和气体动力学等领域[5-9].对于非线性耦合Burgers方程组

(1)

曲娜等[10]仅分析了其差分格式的稳定性而没有考虑计算稳定性.笔者将利用启发性分析方法来推导该非线性耦合Burgers方程组差分格式具有计算稳定性的必要条件.

1 差分格式的表示

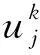
向前差分格式为

(2)

选适当内节点(xj,tk+1)，则该节点处的微分方程组为

向后差分格式为

(3)

2 差分格式计算稳定性的启发性分析

将差分格式进行Taylor展开和自循环消元，转化为等价的变形方程组，即修正微分方程组(Modified PDE).判断该差分格式具有计算稳定性的依据是其修正微分方程组等号右端的二阶导数项为正耗散项，此方法称为MPDE识别法.笔者将MPDE识别法运用于非线性耦合Burgers方程组(1)，以向前差分格式(2)为例进行分析.由Taylor展开，可得

进一步得到如下展开：

(4)

将Taylor展开结果(4)代入向前差分格式(2)，可得

略去上下标后可得

(5)

由方程组(5)可得

对(6)式关于t求微分，可得

(8)

对(6)式关于x求微分，可得

(9)

对(7)式关于x求微分，可得

(10)

对(9)式关于x求微分，可得

(11)

将(7)，(10)，(11)式代入(8)式，可得

(12)

同理

(13)

将(12)，(13)式代入方程组(5)可得向前差分格式(2)的修正微分方程组

同理，向后差分格式(3)的修正微分方程组为

由启发性分析方法可知，只有当差分格式的修正微分方程等号右端的二阶耗散项系数为正时，差分格式才具有计算稳定性；因此有如下结论：

定理1非线性耦合Burgers方程组(1)的向前差分格式(2)具有计算稳定性的必要条件为

定理2非线性耦合Burgers方程组(1)的向后差分格式(3)具有计算稳定性的必要条件为

3 数值实验

由定理1和定理2可知，非线性耦合Burgers方程组(1)的差分格式的计算稳定性仅与u(x,t)和v(x,t)的初值及α，β，Δt有关.现取4个初值进一步验证非线性耦合Burgers方程组(1)的普遍性差分格式的计算稳定性与初值、差分格式结构之间的关系.4个初值分别为：

取α=-1,β=2,-5≤x≤5,0≤t≤1，则非线性耦合Burgers方程组(1)化为

取Δx=0.1,Δt=0.001，左边界值为0，右边界值用Lagrange一次插值方法外插.差分格式的计算稳定性结果列于表1.

表1 差分格式的计算稳定性结果

由表1可知，当α，β，Δt固定时，差分格式的计算稳定性仅与u(x,t)和v(x,t)的初值有关，而不同的初值在x处取不同值时，就得到不同的计算稳定性结果.

4 结语

利用启发性差分格式对一类非线性耦合Burgers方程组的差分格式进行计算稳定性分析，当差分格式的修正微分方程组等号右端的二阶耗散系数大于0时,差分格式是稳定的.非线性发展方程差分格式是否具有计算稳定性，与方程解的性质紧密相关，而本研究中的非线性耦合Burgers方程组差分格式的计算稳定性，依赖于其耗散系数α，β，Δt及初值u(x,0)，v(x,0)的选取.

虽然本研究得到的判断依据只是判断一类非线性耦合Burgers方程组差分格式计算稳定性的必要条件，即差分格式具有计算稳定性必须满足该判断依据，而满足该判断依据的差分格式未必具有计算稳定性；但是，由于在计算中利用该判断依据可以删除不具有计算稳定性的差分格式，避免盲目计算，因此计算稳定性的必要条件是非常有效且实用的.